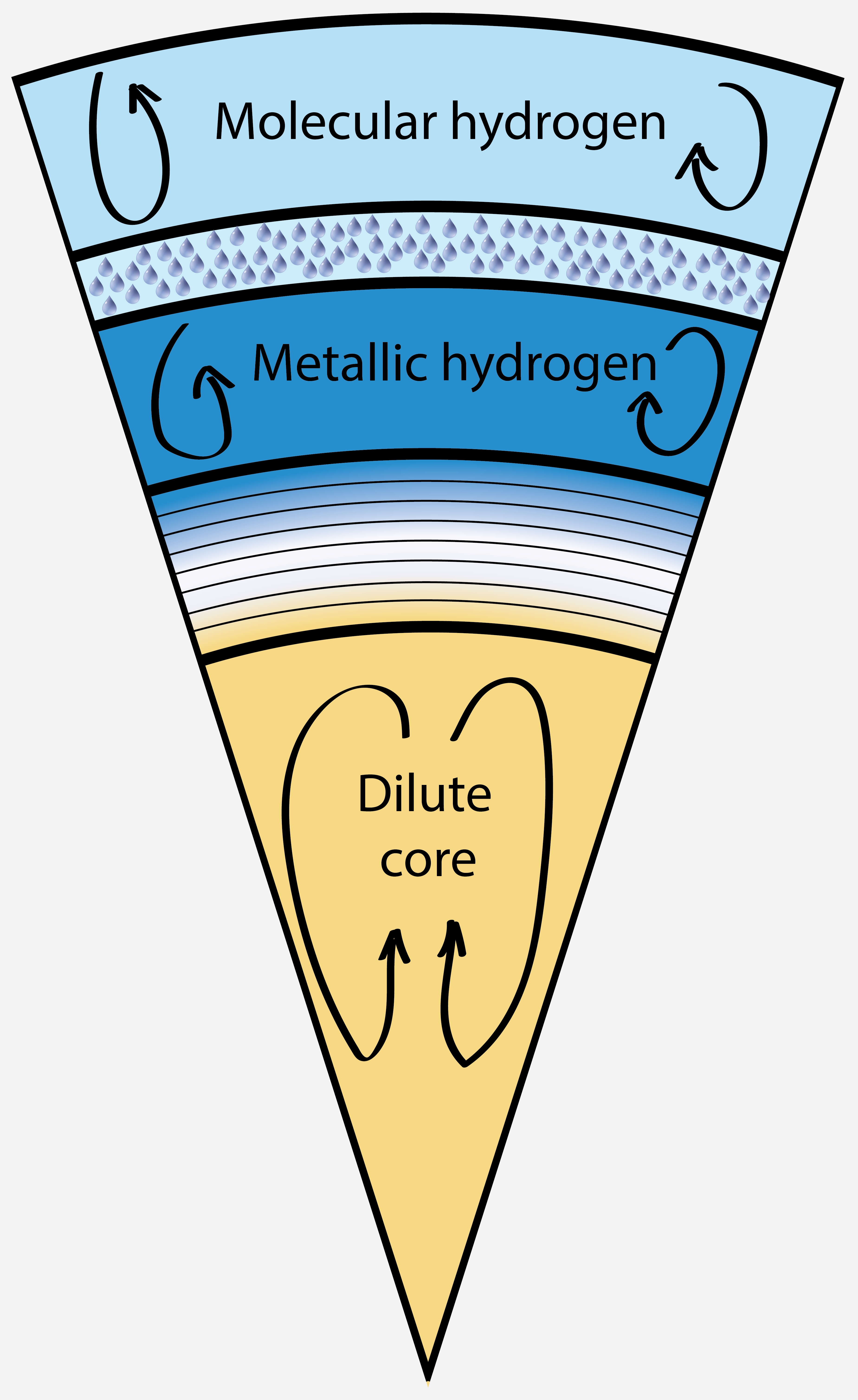
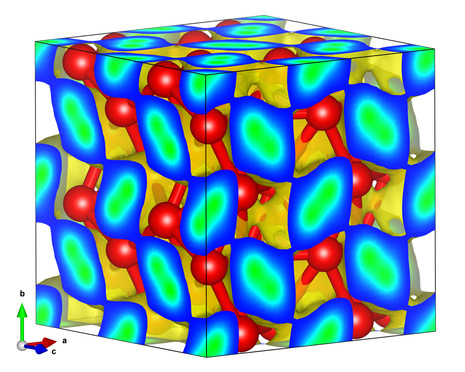
Jupiter's interior structure with helium rain layer and dilute core.
|
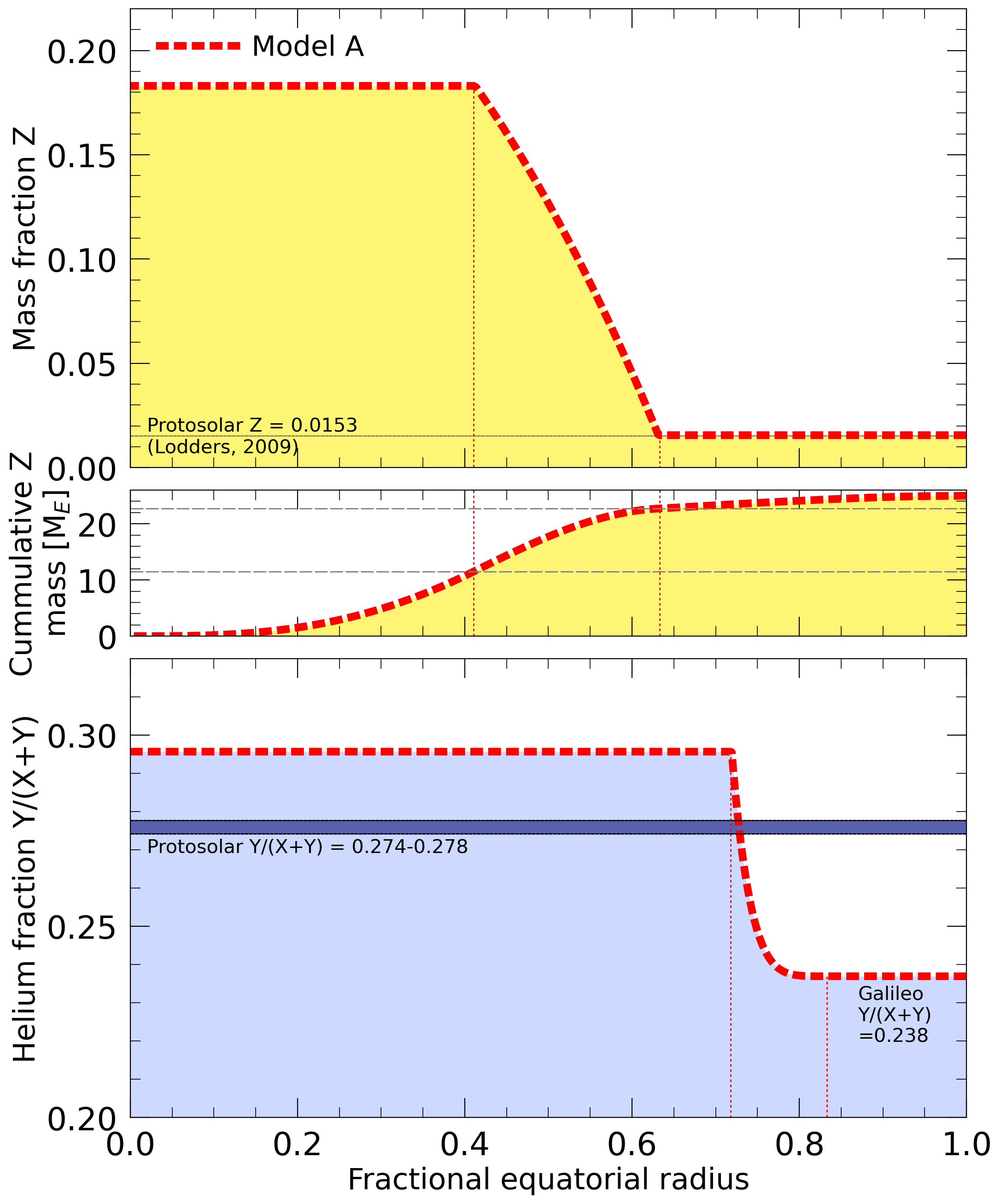
Heavy element (upper panel) and helium mass fractions (lower panel).
|
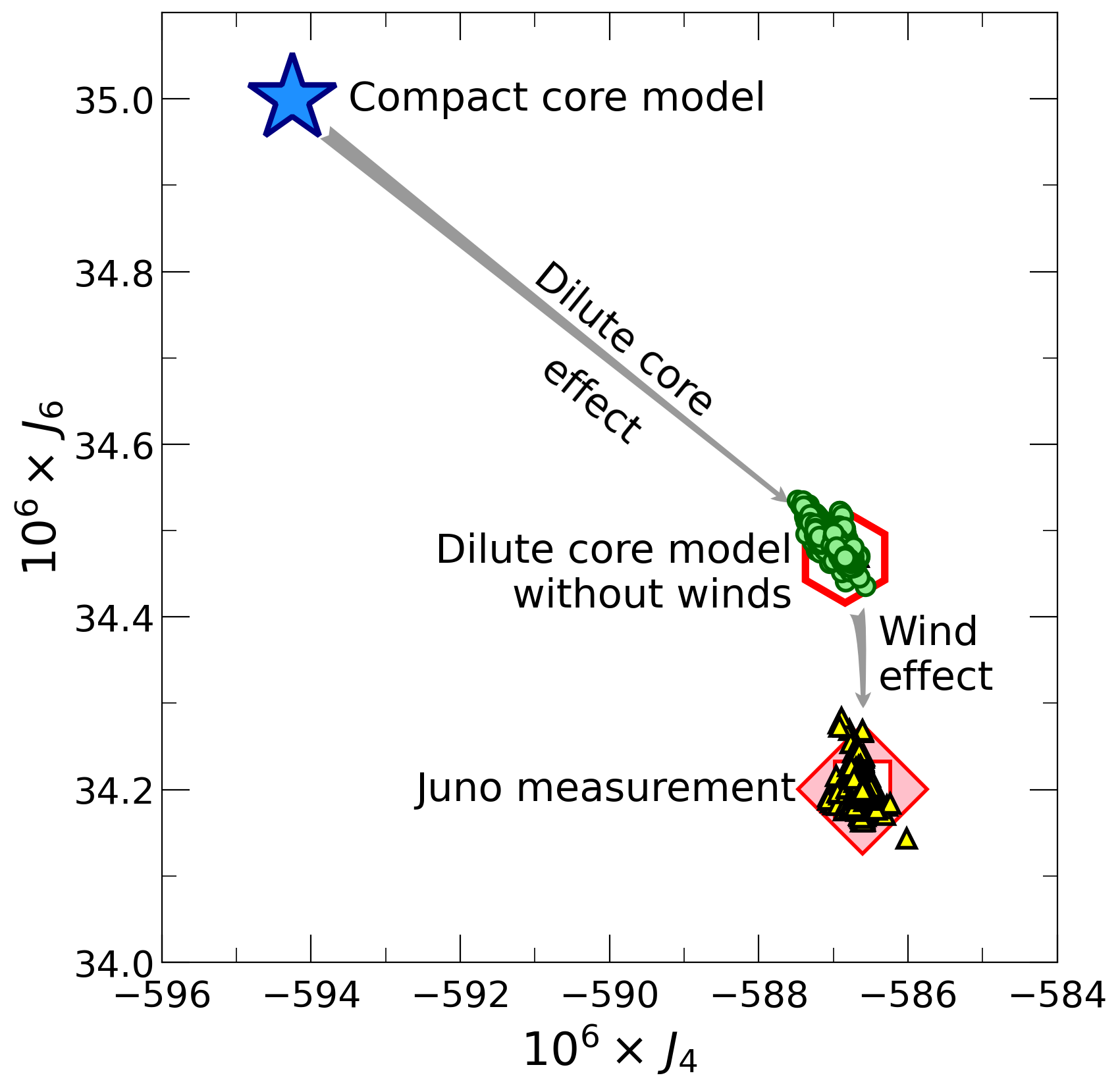
Gravity harmonics J4 and J6 measured by the Juno spacecraft (red diamond) and predicted from models (all other symbols).
|
The Juno spacecraft measured Jupiter's gravity field with exquisite
precision. Matching the measurements with interior models that also
agree findings by the earlier Galileo entry probe and make
physical assumptions about the properties of hydogen-helium mixtures
has been a real challenge. In our latest article, we satisfy
Juno and Galileo measurements for the first time by
constructing Jupiter models with a large dilute core that
extends to 60% of the planet's radius (left and middle panels). We
predict the dilute core to be comprised of 58% hydrogen, 24% helium,
and only 18% of heavier elements. The dilute core reduces the magnitudes of
the gravity harmonics J4 and J6 (right panel) so
such an extent that we can match the spacecraft measurements with wind
models that we optimize simultanesouly with model parameters for the
interior. Our dilute core is homogeneous and convective. So we predict
it to contribute to the generation of Jupiter's magnetic field in
addition to the metallic hydrogen layer. Having two interacting dynamo
layers may help explain the structure of Jupiter's magnetic field.
|
|
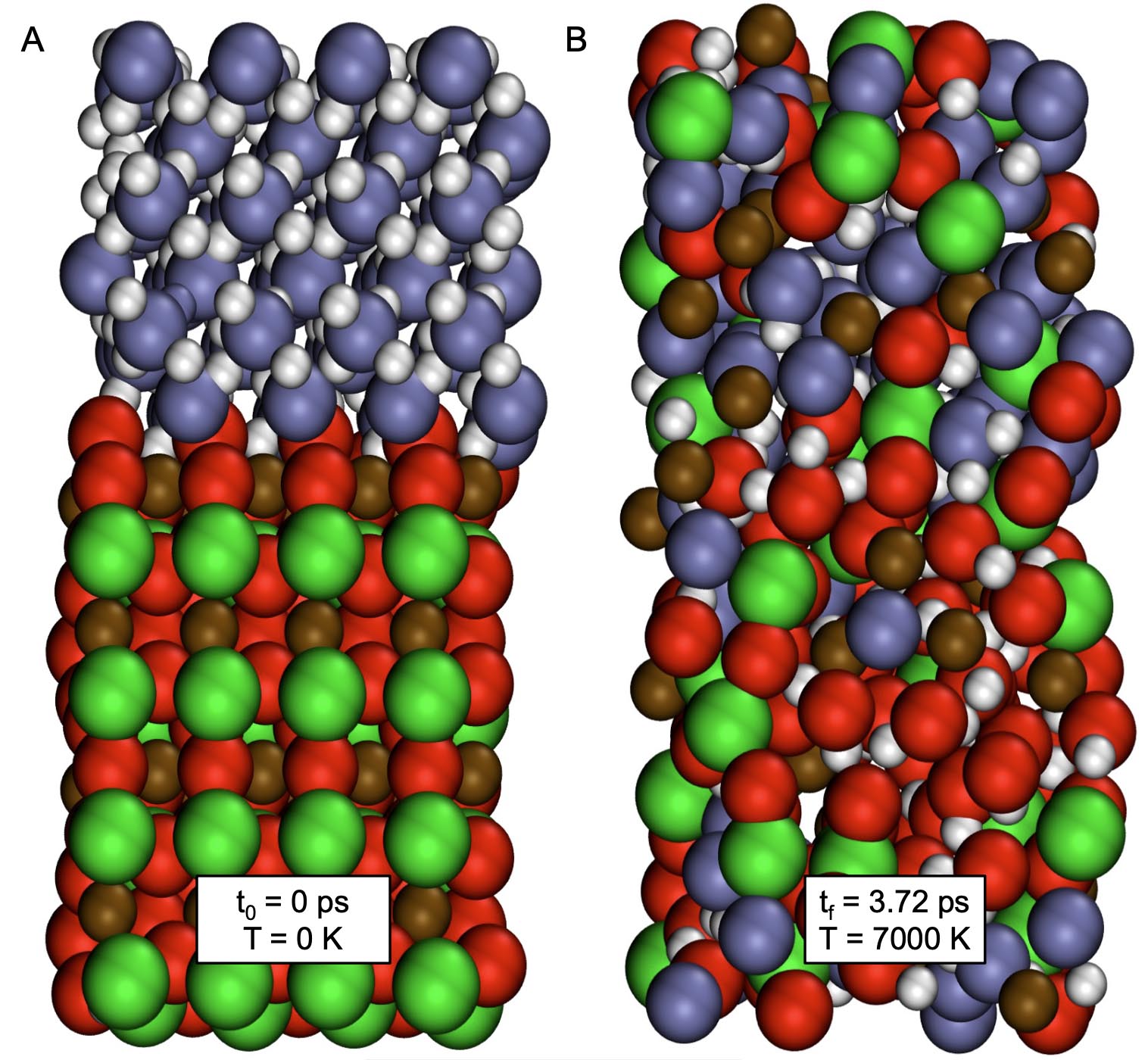Initial and final configurations of ab initio simulations of rock-ice mixtures.
|
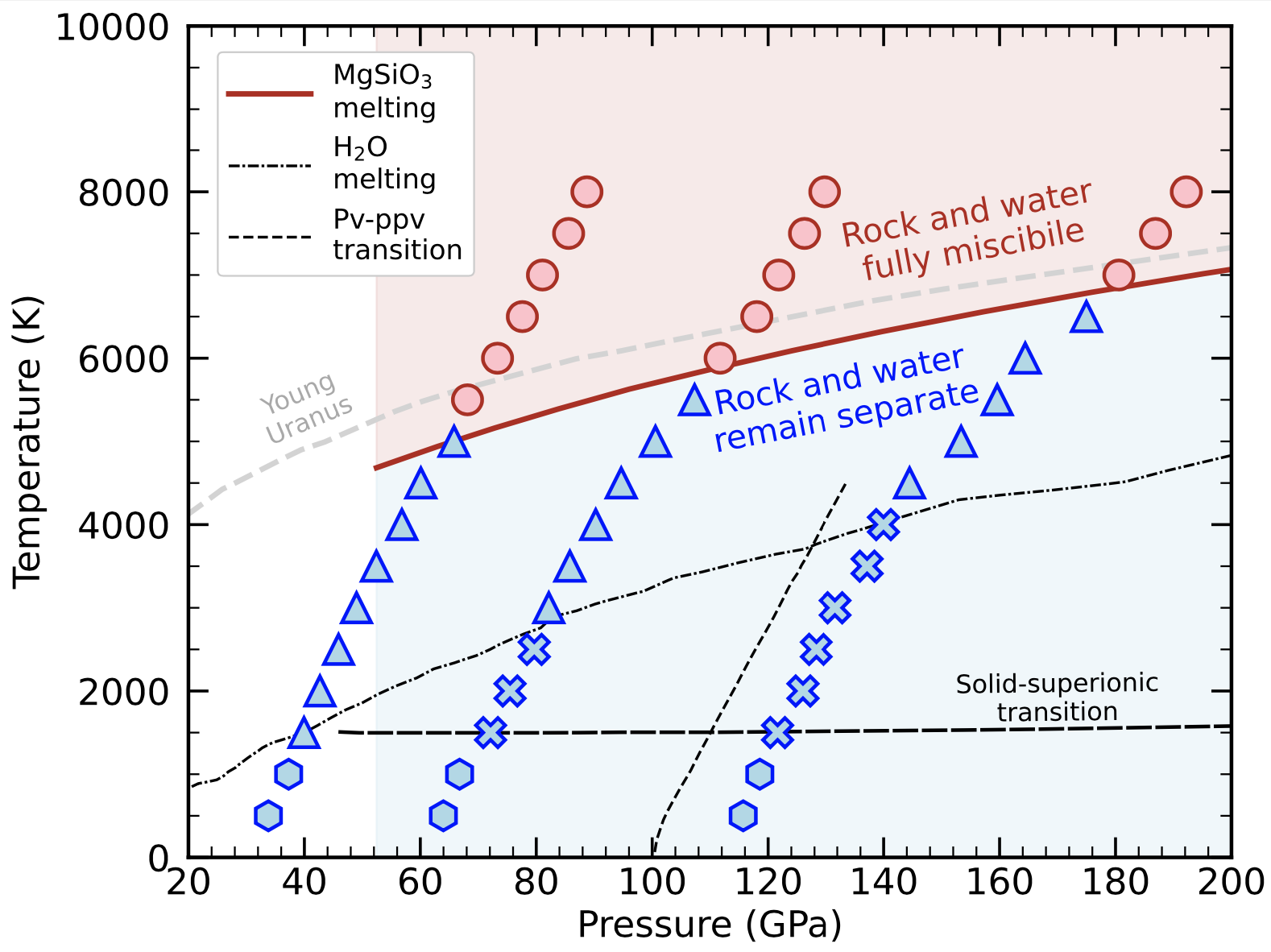Pressure-temperature conditions where rock and ice remain separate (blue) or mix (red) in all proportions.
|
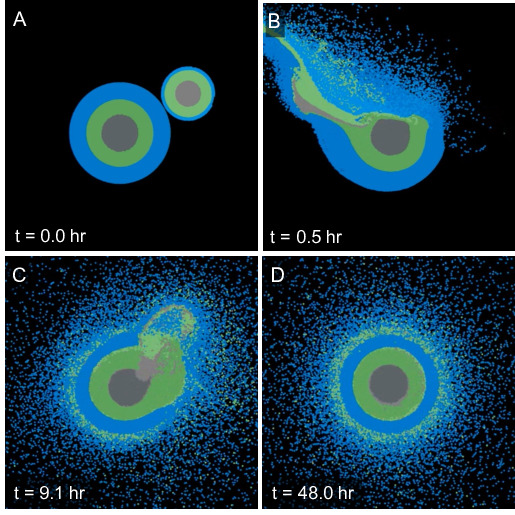Simulation of planet size imacts illustrating that rock and ice mix dynamically.
|
In our latest article, T. Kovacevic, F. Gonzalez-Cataldo, S. T. Stewart, and I study conditions in the interiors of water world planets that are expected to contain large amounts of rock and ice. We focus on the question whether they have well separated layers or rock and ice or if they likely have mixed rock-ice layers. First we performed ab initio computer simulations (upper left diagram) and determined rock and ice mix in all proportions as soon as the temperatures become sufficiently high for rock to melt (upper center). Finally we perform planet-size impact simulations (upper right) with the SPH method to demonstrate that such conditions are reached when giant impacts occur during a planet's formation. We conclude of water world planets likely have mixed layer when they form but it yet remains to be determined how long such layers last.
|
|
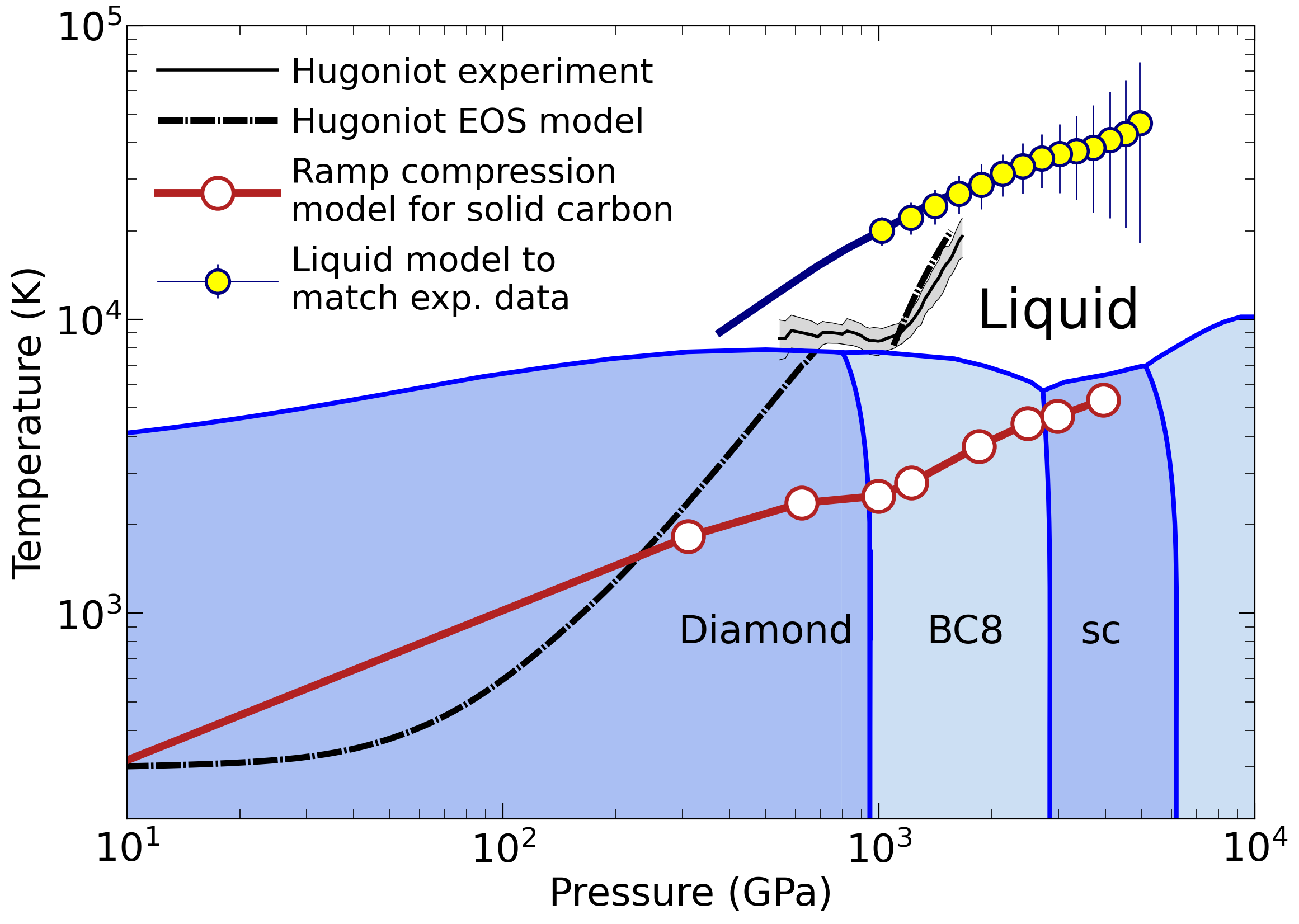
Phase diagram of carbon with liquid and solid model for ramp compression experiments
|
In our latest article, F. Gonzalez-Cataldo, B.K. Godwal, K. Driver, R. Jeanloz, and I study with computer simulations a material becomes during ramp compression experients. The work was motivated by the ramp compression experiments on diamond by R. Smith et al. that reached stress conditions of several tera Pascals. We found that for a given density, the measured stresses were too high to be compatible with results from ab initio simulations. The measured density-stress point can be matched with simulation results of liquid carbon (yellow symbols). This assumes the diamond samples melted during compression, which is under debate. There was sufficient energy in the experiment for this occur but no evidence for it was collected during the measurements. Later experiments by A. Lazicki et al. demonstrated that carbon remained solid.
So we derive a multi-step model for ramp compression of solid carbon (red circles). For a assumed step number and size, this models allow us to estimate how much plastic work occured during the ramp compression.
|
|
|
|
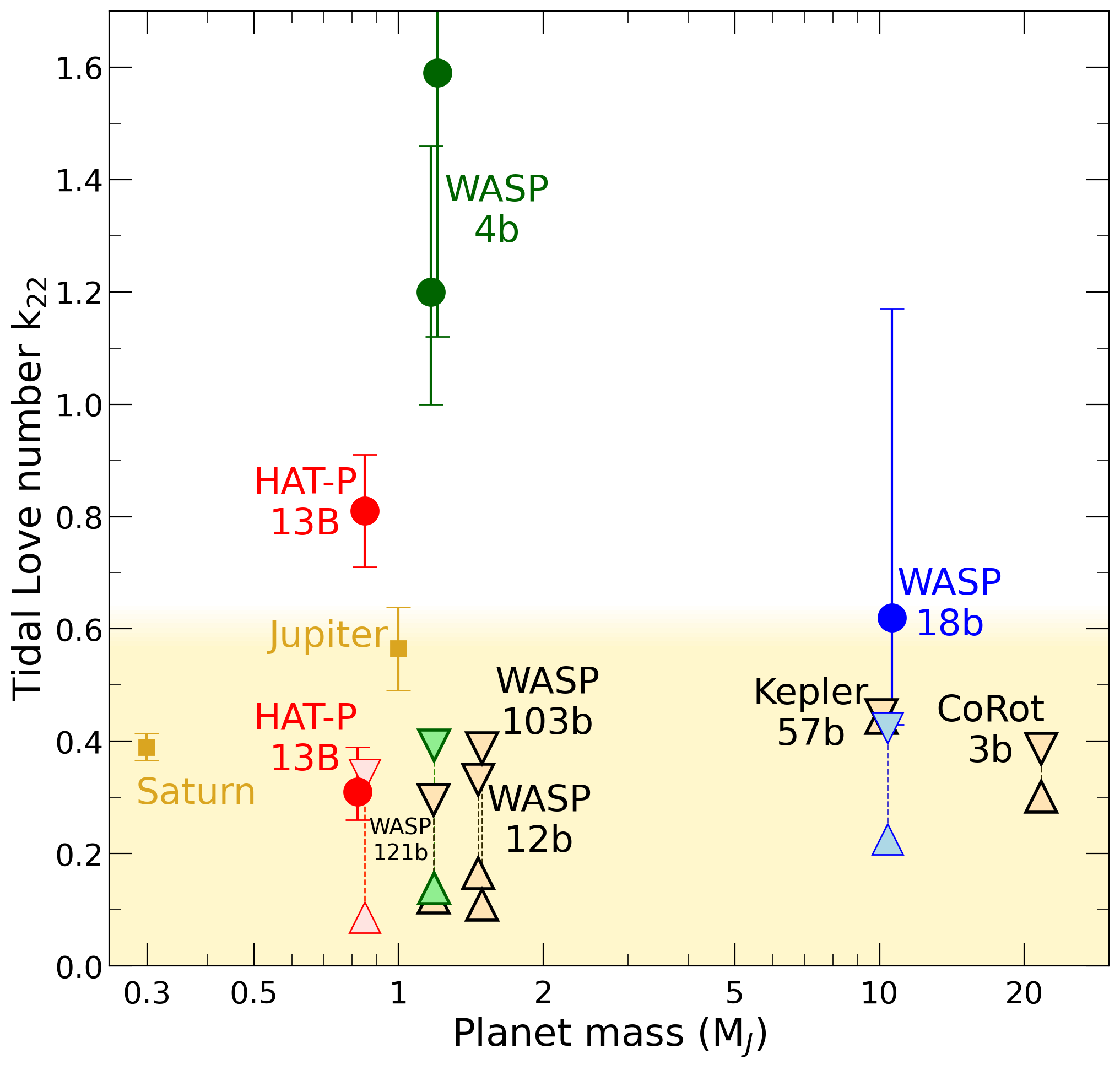
Tidal Love numbers from observations (solid cirlces) and our model predictions (open triangles) are compared for a series of exoplanets.
|
In our latest article, we study how the shape and gravity field of strongly irradiated, giant exoplanets is destorted by the external gravity field of their massive host stars. A planet's response to such external fields is expressed by the tidal Love number, k22, which has been inferred from telescope observations for the exoplanets WASP 4b (green color), HAT-P 13b (red), WASP 18b (blue). In the digram on the left, we compared these observations (solid circles) with our calculated values that we represent with triangles of corresponding colors. The upper triangles represent models without rocky core while the lower triangles show predictios for the largest possible cores. The beige symbols show our predictions for the exoplanets WASP 12b, 103b, 121b, Kepler 57b, and Corot 3b. We find that the static Love number, k22 cannot exceed the value 0.6 (yellow shaded region), which is in contradiction with some of the observations. We suggest additional observations to be made and existing data to be re-analyzed because this discrepancy may imply that the orbits of the observed exoplanets could be affected by other factors like not-yet-detected exoplanets. In our paper, we also derived the gravity harmonics, shape, of moment of inertia for our planet models.
|
|
|
|
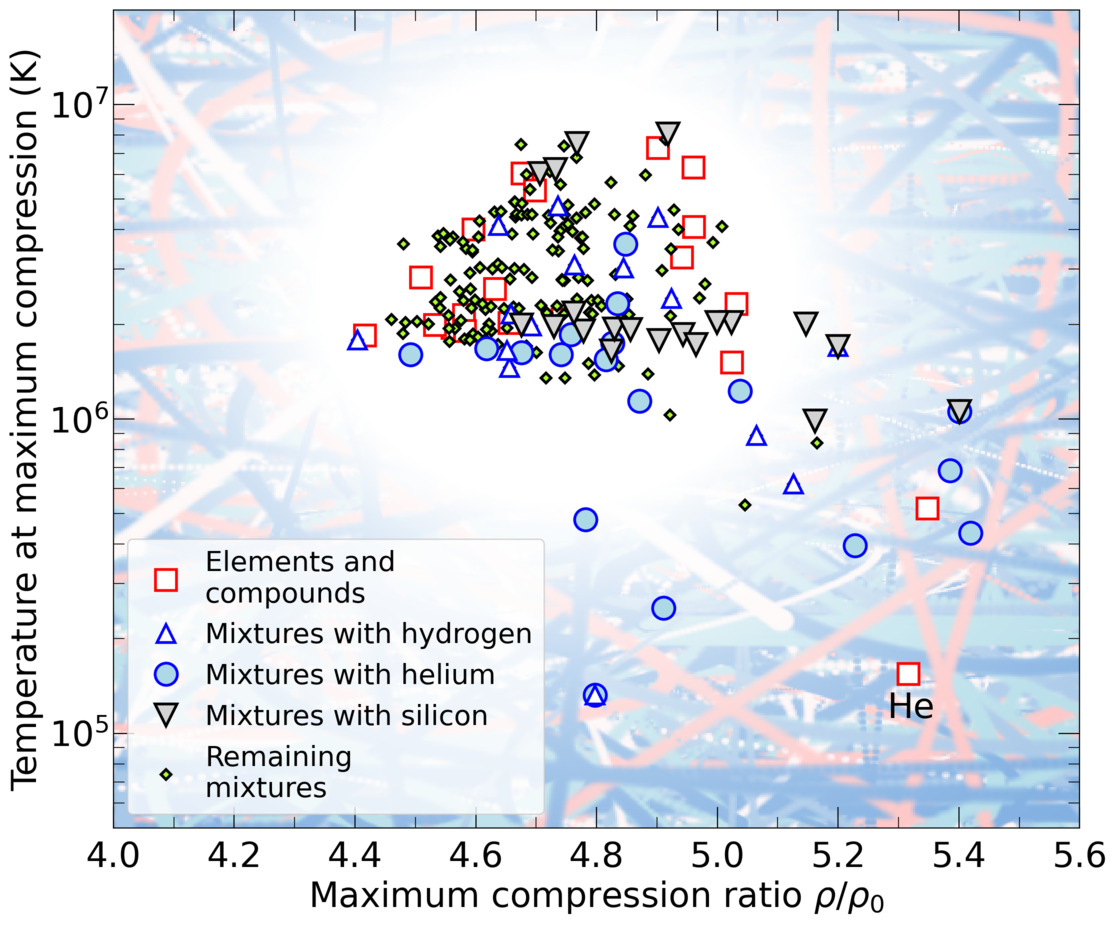
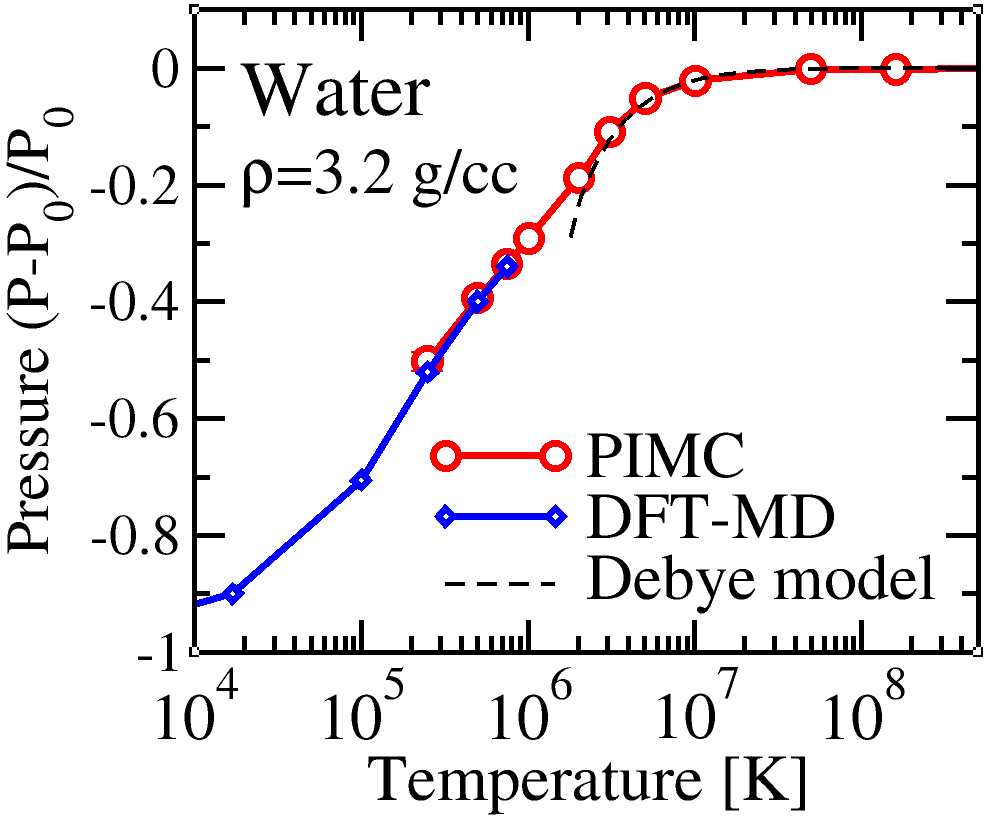
States of maximal shock compression of 200 compounds and mixtures predicted by our FPEOS database.
|
With the goal of making warm dense matter computations more reliable and efficient, we make available our first-principles equation of state (FPEOS) database for materials at extreme conditions. We provide our EOS tables the elements H, He, B, C, N, O, Ne, Na, Mg, Al, and Si as well as the compounds LiF, B4C, BN, CH4, CH2, C2H3, CH, C2H, MgO, and MgSiO3 that are solely based on results from ~5000 path integral Monte Carlo and density functional molecular dynamics simulations. For all these materials, we provide the pressure and internal energy over a density-temperature range from ~0.5 to 50 g/cc and from ~104 to 109 K. In our recent article, we compute isobars, adiabats, and shock Hugoniot curves in the regime of L and K shell ionization. Invoking the linear mixing approximation, we study the properties of mixtures at high density and temperature. We derive the Hugoniot curves for water and alumina as well as for carbon-oxygen, helium-neon, and CH-silicon mixtures. We predict the maximal shock compression ratios of H2O, H2O2, Al2O3, CO, and CO2 to be 4.61, 4.64, 4.64, 4.89, and 4.83, respectively. Finally we use the FPEOS database to determine the points of maximum shock compression for all available binary mixtures (left graph). We provide all FPEOS tables as well as C++ and Python computer codes for interpolation, Hugoniot calculations, and plots of various thermodynamic functions.
|
|
|
|
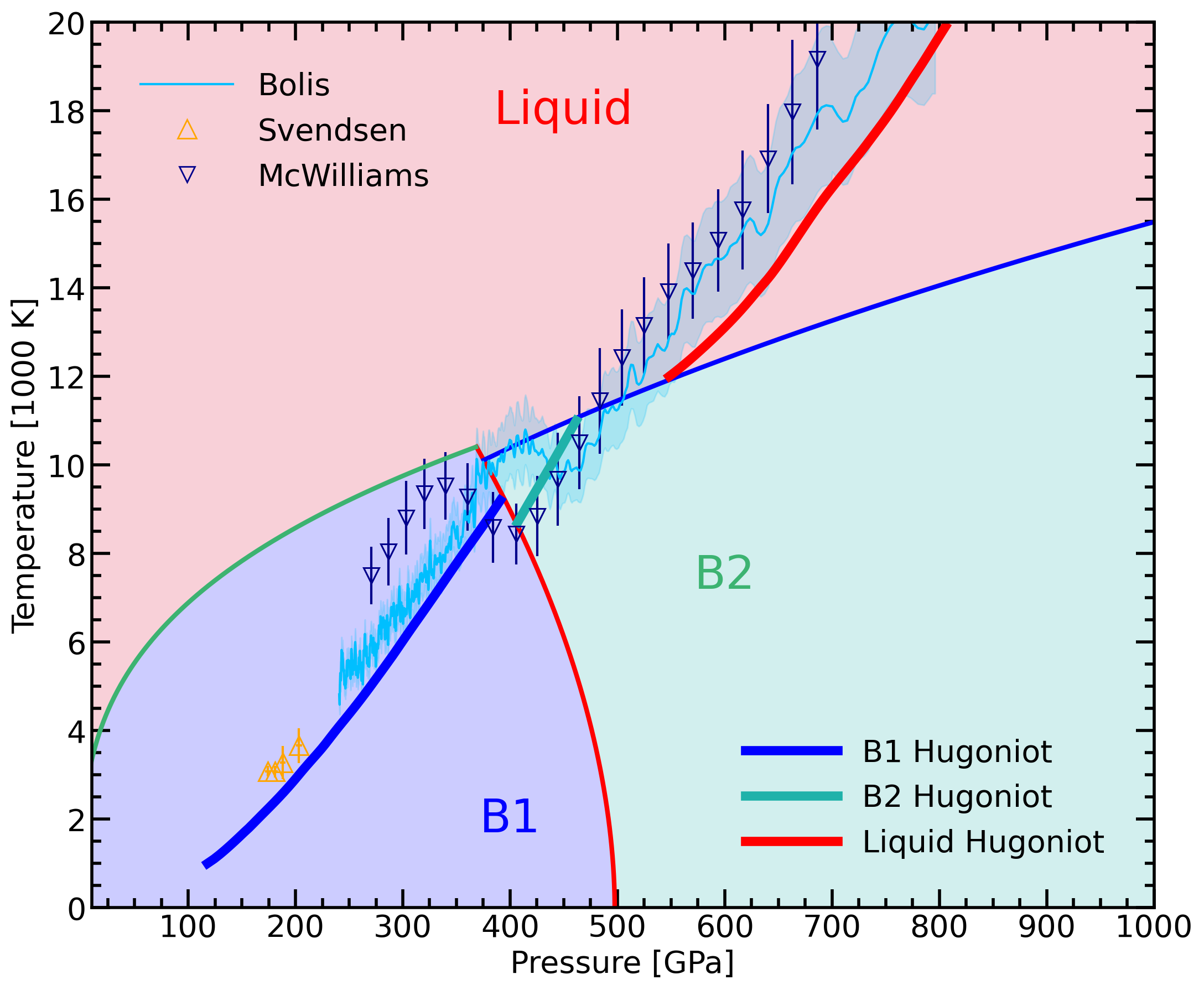
Phase diagram of MgO with liquid and solid B1 and B2 phases. Theoretical and experimental shock Hugoniots curves are compared.
|
With density functional molecular dynamics simulations, we computed the phase diagram of MgO in the pressure range from 50 to 2000 GPa up to temperature of 20000 K. Via thermodynamic integration (TDI), we derive the Gibbs free energies of the B1, B2, and liquid phases and determine their phase boundaries. The B1 structure is a NaCl-type crystal, in which Mg and O nuclei occupy alterating sites. Each atomic species by themselves forms a face-centered cubic lattice. In the B2 structure, is a CsCl-type crystal. Each atom species by themselves form a simple cubic structure. With our computer simulation, we show that anharmonic effects stabilize the B1 phase. We predict the B1-B2-liquid triple point to occur at approximately T = 10000 K and P = 370 GPa, which is higher in pressure than was inferred with quasi-harmonic methods. We predict the principal shock Hugoniot curve to enter the B2 phase stability domain but only over a very small pressure-temperature interval. This may render it difficult to observe this phase with shock experiments because of kinetic effects. Here are a copy of our article and a few slides in PPTX and PDF formats available to download.
|
|
|
|
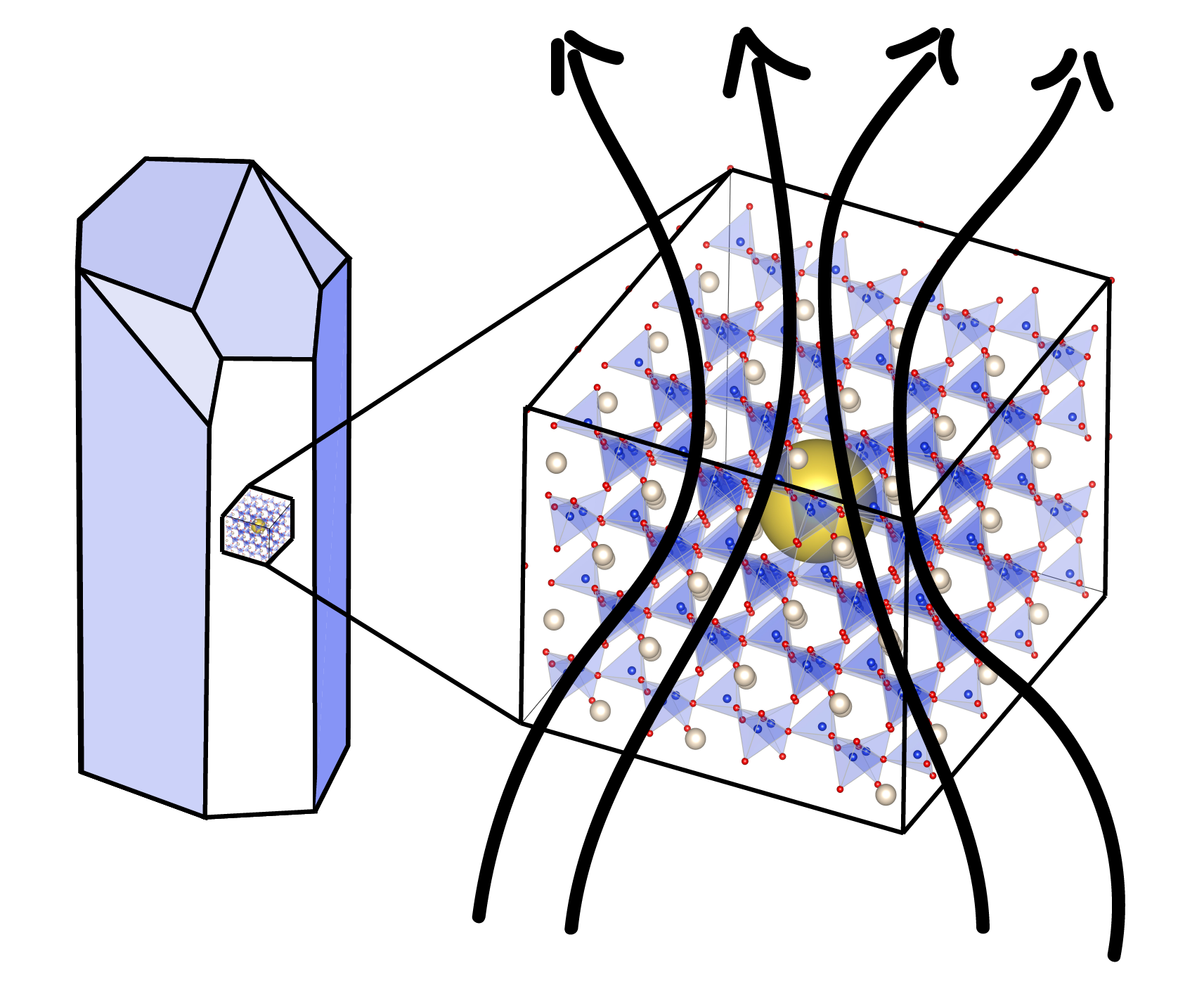
Nanopore (yellow) in quartz crystal that may serve as a reservoir of helium atoms.
|
This joint theoretical-experimental project was sparked by a drastic disagreement between laboratory data and results from computer simulations for the diffusion of helium atoms in quartz crystals. This is important because the diffusion of noble gases in minerals is often utilized to reconstruct the thermal histories of rocks. Computer simulations of helium in perfect quartz crystals predicted that already at room temperature, all helium atoms would diffuse out of the crystal because the helium atoms encounter very lower energy barriers along the crystal's z channel. Taken at face value, this would imply all helium would have diffused out of the crystal before the experiments even began. Conversely, however, the lab measurements showed that temperatures between 70 and 220 oC were required for most helium atoms diffuse out of quartz crystals. In our article, this discrepancy is resolved by introducing the novel hypothesis that helium atom reside inside nanopores in the quartz crystal. The calculations showed that activation energy for helium atoms to diffuse from the nanopore into the crystal matched experimental data. A consistent effective diffusion model was constructed and the nanopore concentration was estimated to be approximately 10-5.
|
|
|
|
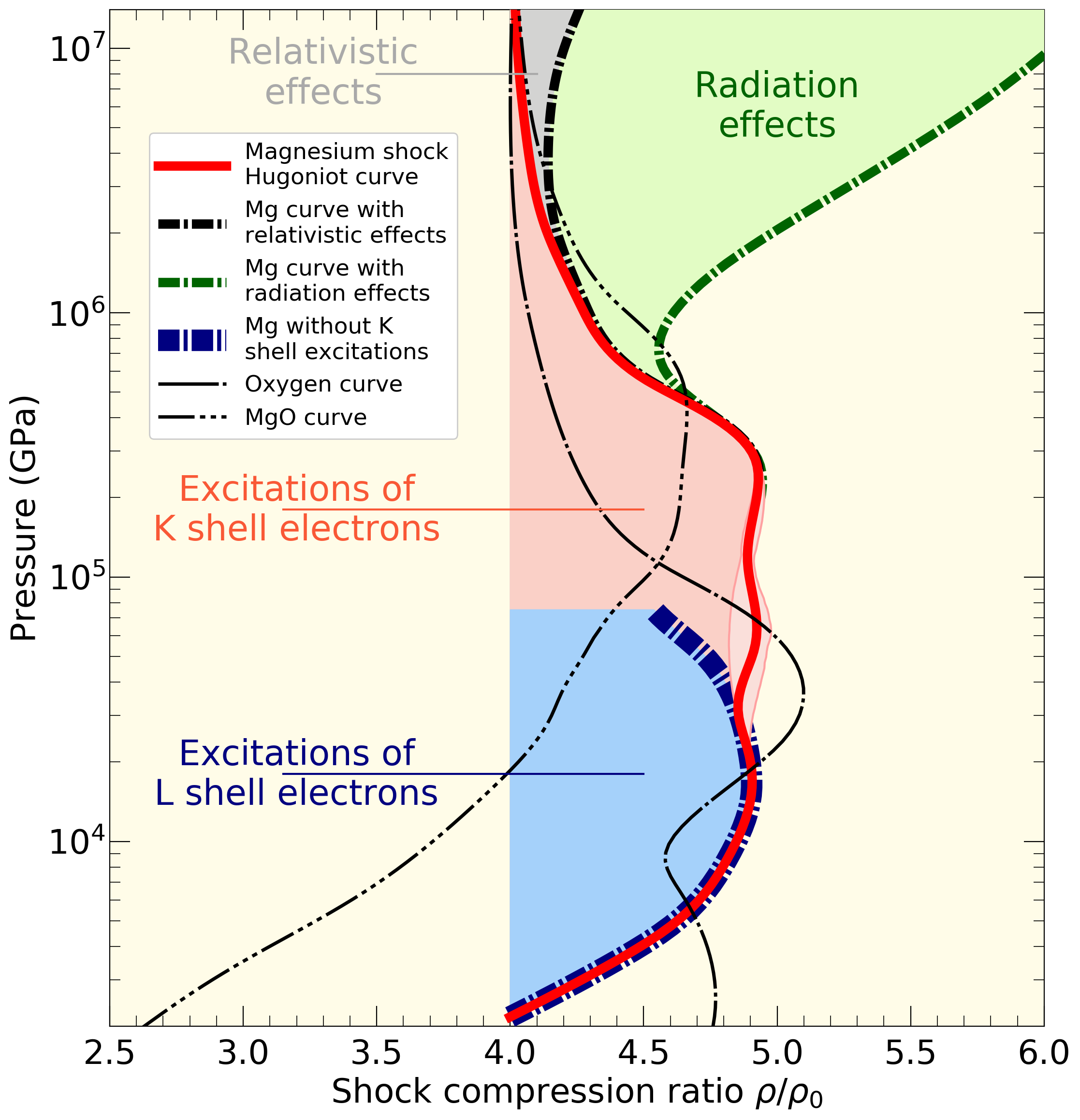
Four excitation mechanisms that control the shock Hugoniot curve of magnesium are plotted in pressure-density space.
|
In our latest article about warm dense matter, we employ path integral Monte Carlo and density function molecular dynamics simulations to study the properties of hot, dense magensium at high temperature and density. On the left, we show our prediction for the principal shock Hugoniot curve, which will most likely be the first quantity to be measure when laboratory experiments reach these conditions in the future. We identify four main excitation mechanisms that control the density that is reached in these compression experiments. In the low-pressure regime, excitations of L-shell electrons increase the shock compression ratio above the canonical value of 4. At higher pressure, the excitations of K-shell electrons maintain a high compression ratio of about 4.9. The compression ratio starts to decrease again once all K-shell electrons have been ionized. However, this decrease in compensated by the onset of radiative effects. Photons that are spontaneously emitted start making substantial controbutions to the energy and pressure. In compression, relativistic effects, that increase the energy of the electrons, play only a minor role.
|
|
|
|
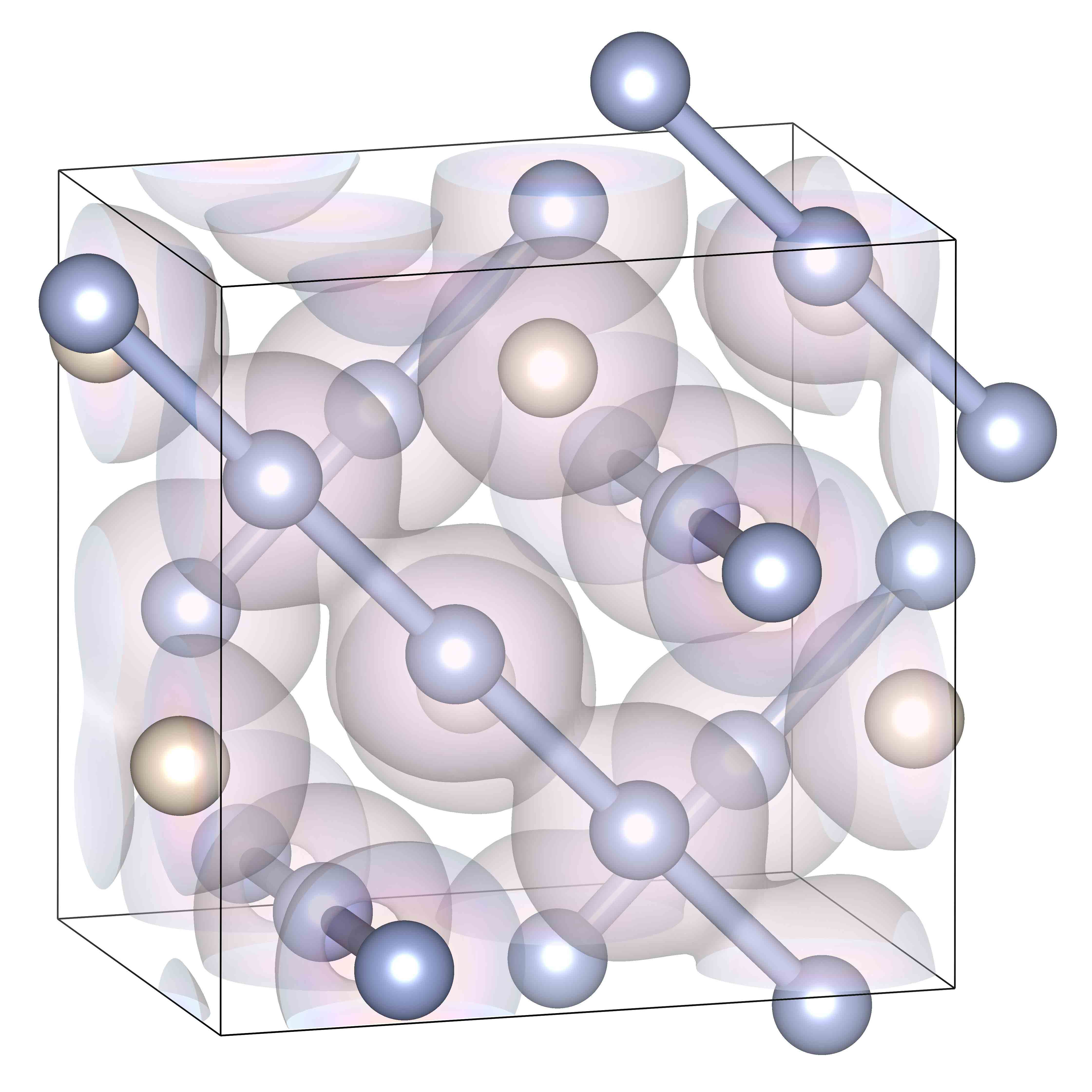
Novel high-pressure structure of fluorine. Here are two alternate views A and B.
|
At the ambient conditions, fluorine is a highly reactive molecular gas. However, at high pressure, its properties change in a remarkable way. In our latest article, Mark Olson, Shefali Bhatia, Paul Larson and I use computer simulations to predict that fluorine forms a polyermic and metallic structure at 31 Mbar. Instead of the usual diatomic F2 bonding, the three quarters of the F atoms (blue) in the structure on the left are arranged in a 3D set of chains. The remaining quarter of atoms (red) occupied voids in between these chains. While flourine typically does not conduct electricity, our new high-pressure structure is an excellent conductor.
We obtained these results with a novel computer algorithm that allows us to efficiently predict crystal structures under symmetry and geometric constraints. We compare fluorine, chlorine and iodine and make reference to X-ray diffration experiments.
|
|
|
|
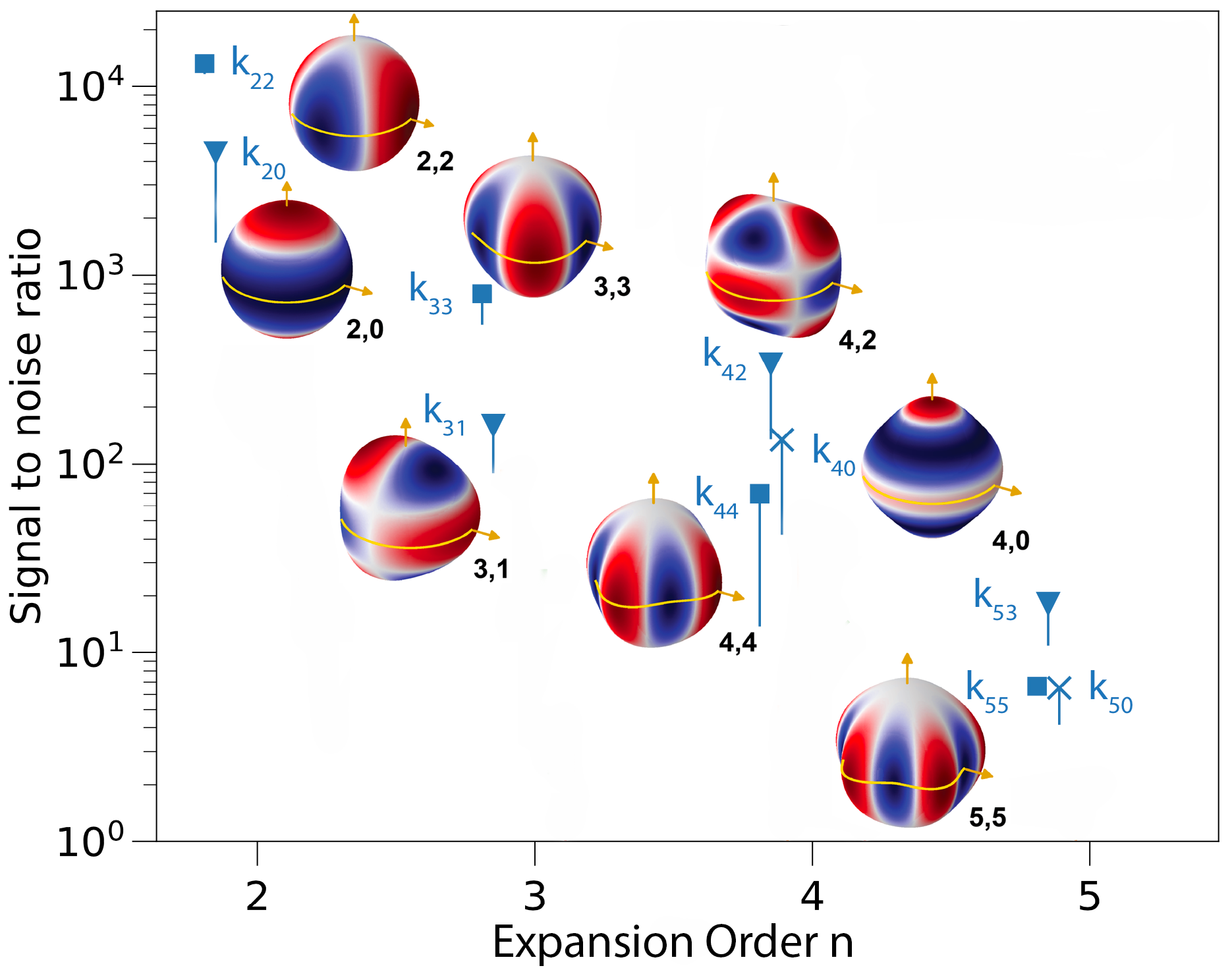
Signal to noise ratio for dectecting Jupiter's response to tidal forces from Io with the Juno spacecraft.
|
The four Galilean satellites, Io, Europa, Ganemede, and Callisto as
well as the sun all change the shape of Jupiter very slighly through
their gravitational forces. In this paper, we
calculate the strengh of this tidal response, which is represented as a series of Love numbers (knm).
We determine which Love numbers can be detected with the Juno spacecraft in the course of the on-going mission.
The graph on the left suggests that Io's k22, k33, k42, and k31 lead to
strong signals and should thus all be detectable. We predict a remarkably small range for Io's equilibrium Love
number k22 = 0.58976 ± 0.0001. Any deviation from this prediction can then be attributed with dynamic tidal effects.
|
|
|
|
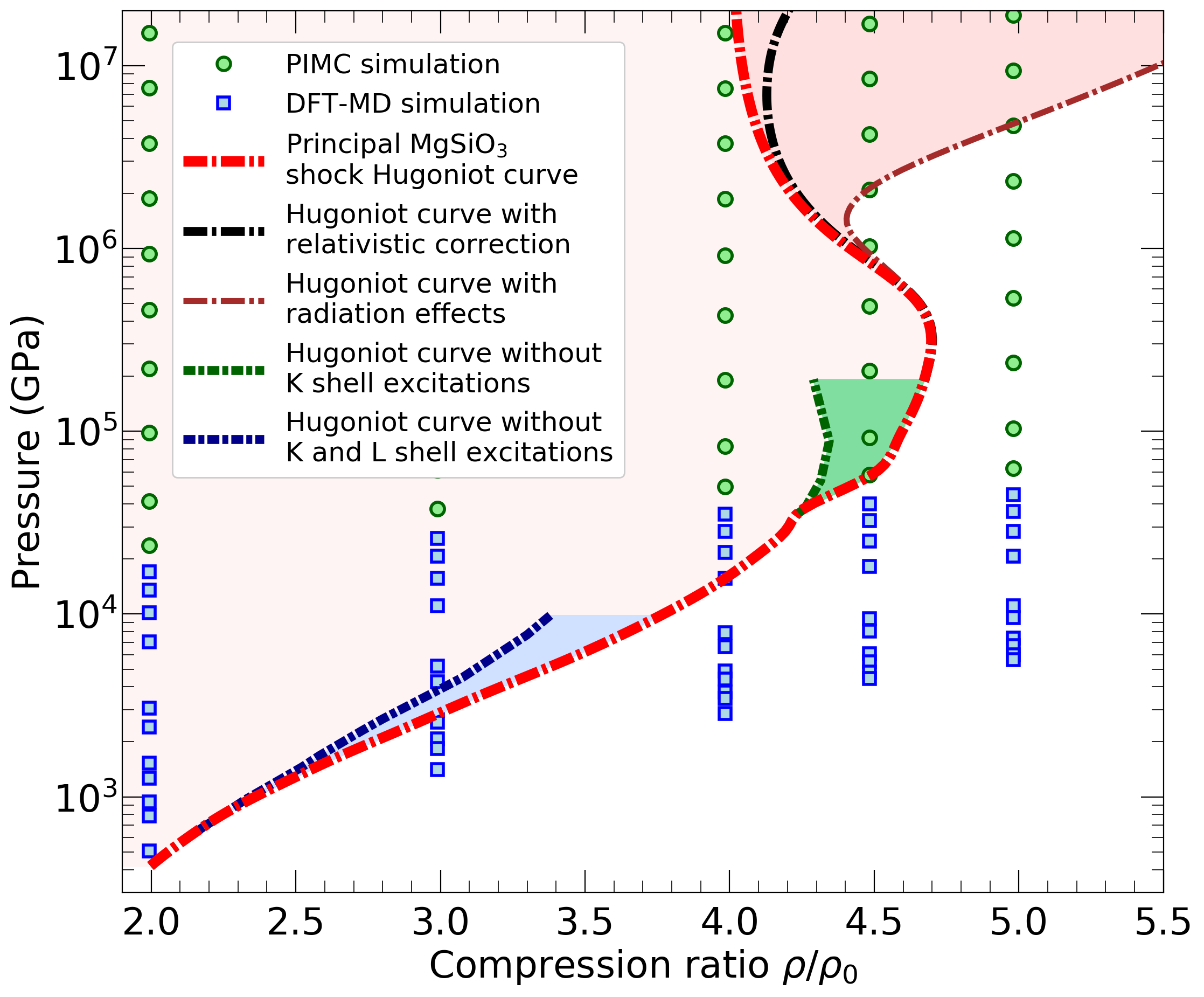
K shell (blue shade) and L (green shade) shell ionization effect on shock Hugoniot curve of MgSiO3.
|
Late during solar system formation, rocky planets
grow through massive impacts. The shock Hugoniot curve characterize
how hot and dense the rocky mantle becomes during an impact. In two
recent papers, we determined the shock Hugoniot curves of
MgO and
MgSiO3 with path
integral and density functional molecular dynamics simulations. In the
graph on the left, we show how the ionizations of K and L shell electrons
increases the density during an impact event. We also provided equation
of state tables over a large range of density-temperature conditions
for both materials.
|
|
|
|
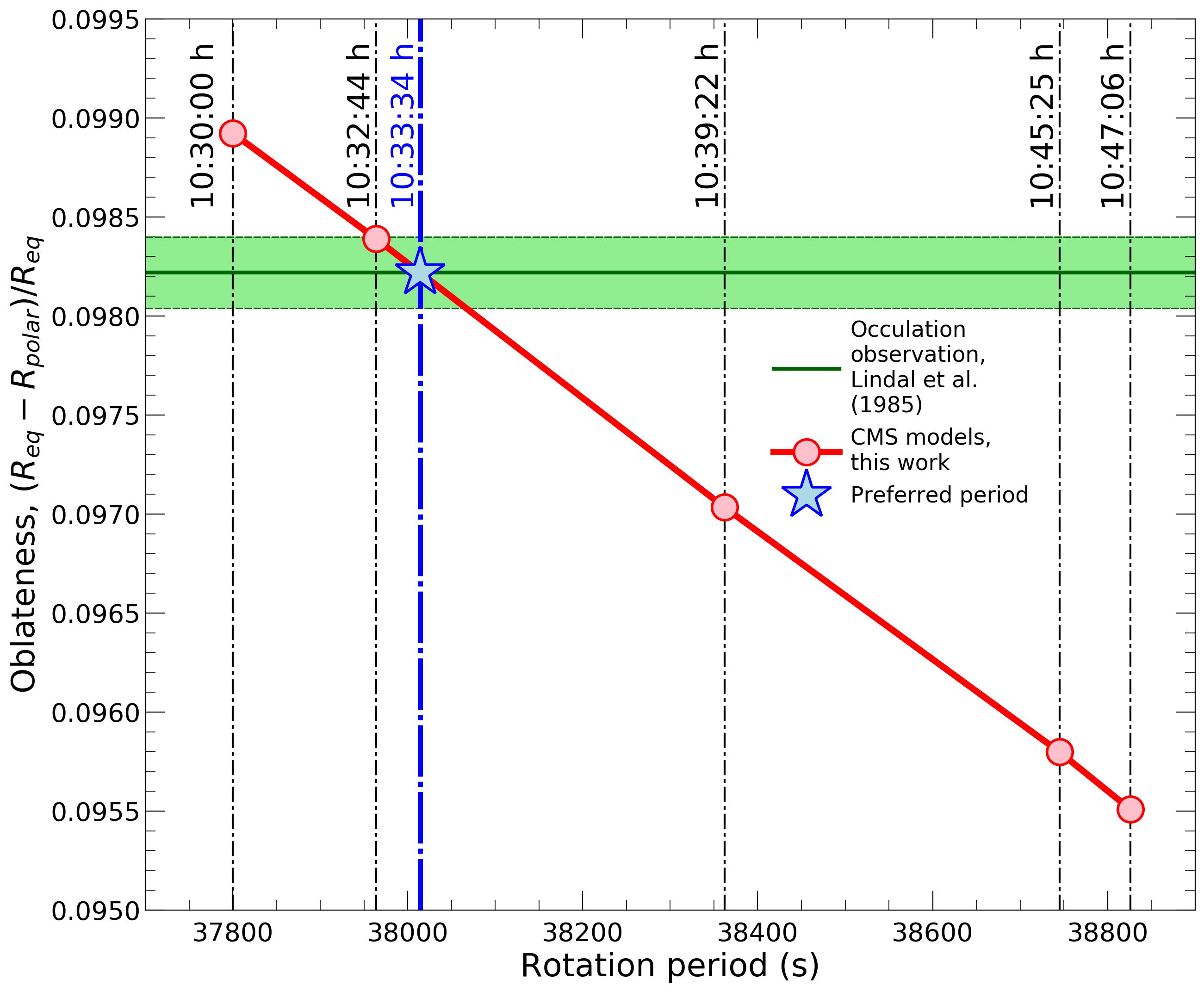
The graphs shows that only a rotation period of 10:33:34h ± 55s is compatible with the observed oblateness.
|
Saturn's rotation period cannot be measured directly
and has thus been very uncertain. Estimates vary between 10:32:45 h and
10:47:06 h, which is an uncomfortably large range that introduces
uncertainties into the analysis of various spacecraft measurements and
remote observations. The rotation period cannot be derived from
Saturn's magnetic field because it is perfectly aligned with the planet's
axis of rotation. This is not case for Jupiter and its rotation period
has been determined precisely to be 9:55:27 h. In our latest article, we combined
gravity data from the Cassini mission and Voyager's measurements of
the planet's shape to determine a rotation period of 10:33:34 h
± 55 s. The faster a planet rotates to more oblate it becomes,
which enabled us to infer its rotation period.
For this analysis,
we developed an accelerated version of the Concentric MacLaurin
Spheroid (CMS) method that enabled to constructed Monte Carlo
ensembles of plausible interior models. We currently apply this
approach to construct models for Jupiter's interior to match gravity
measurements by the Juno spacecraft. |
|
| |
Planet Saturn was born naked but today it has rings and winds 9000 km deep.
|
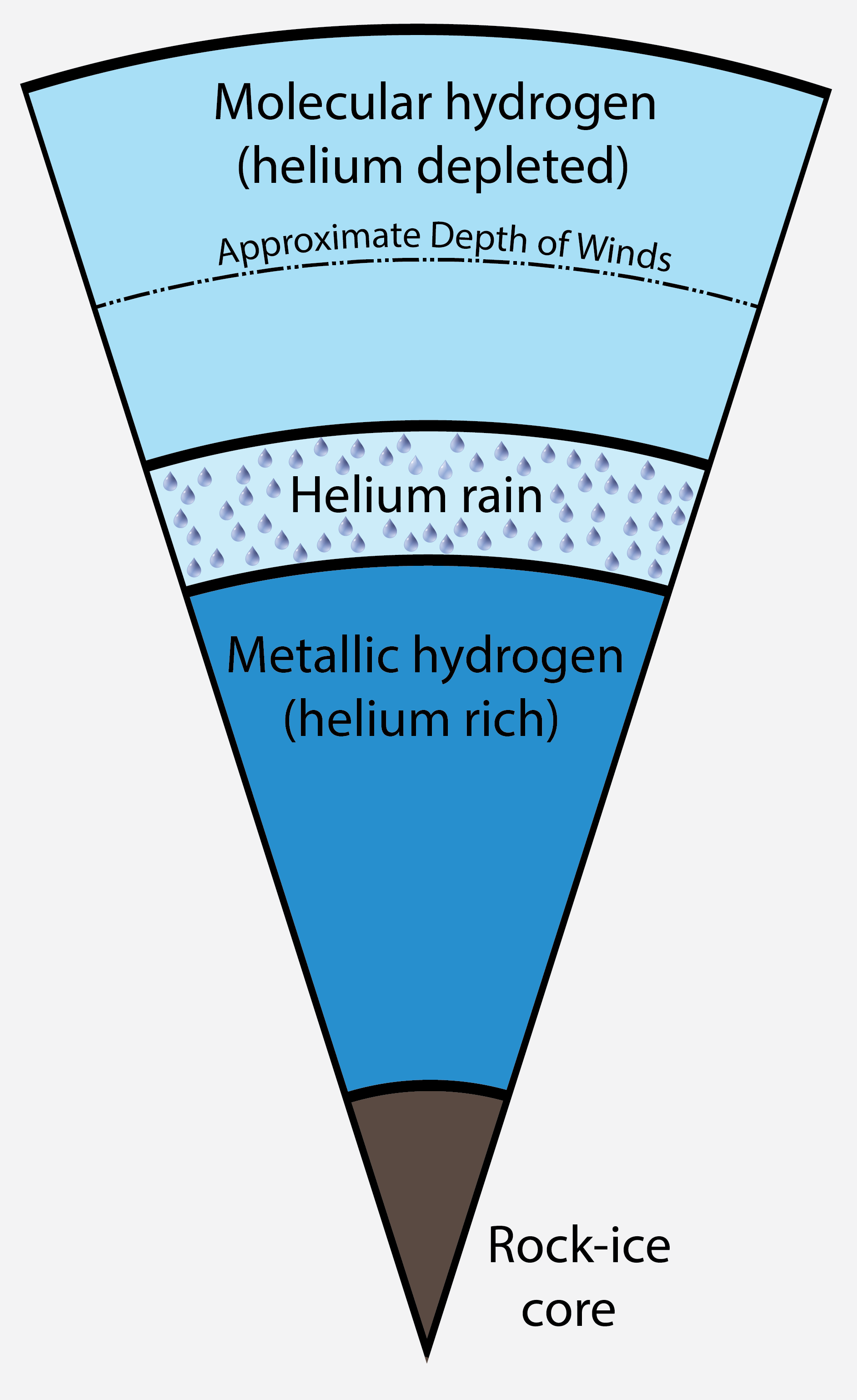
Layers in Saturn's interior.
|
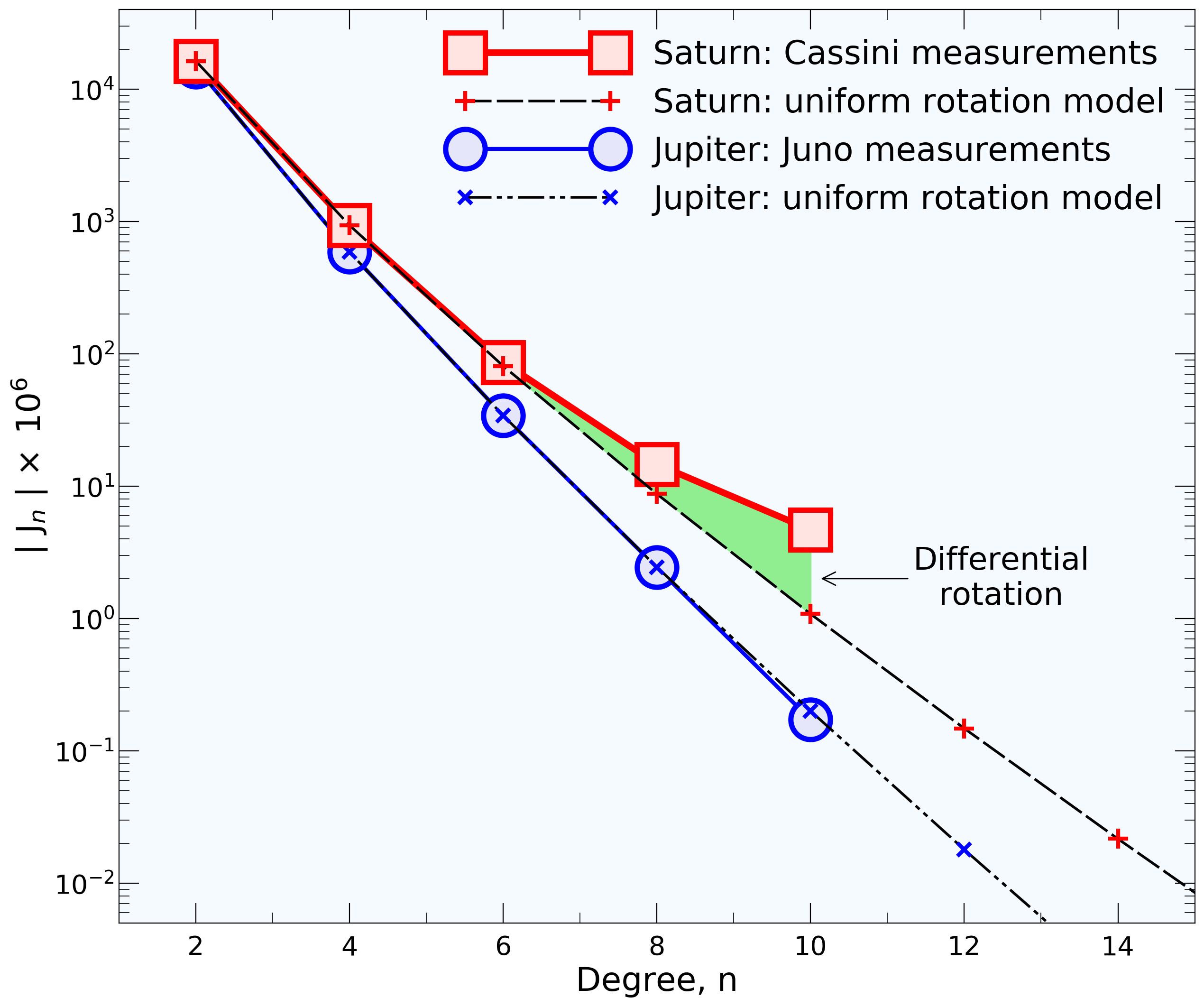
Gravity coefficients of Saturn and Jupiter.
|
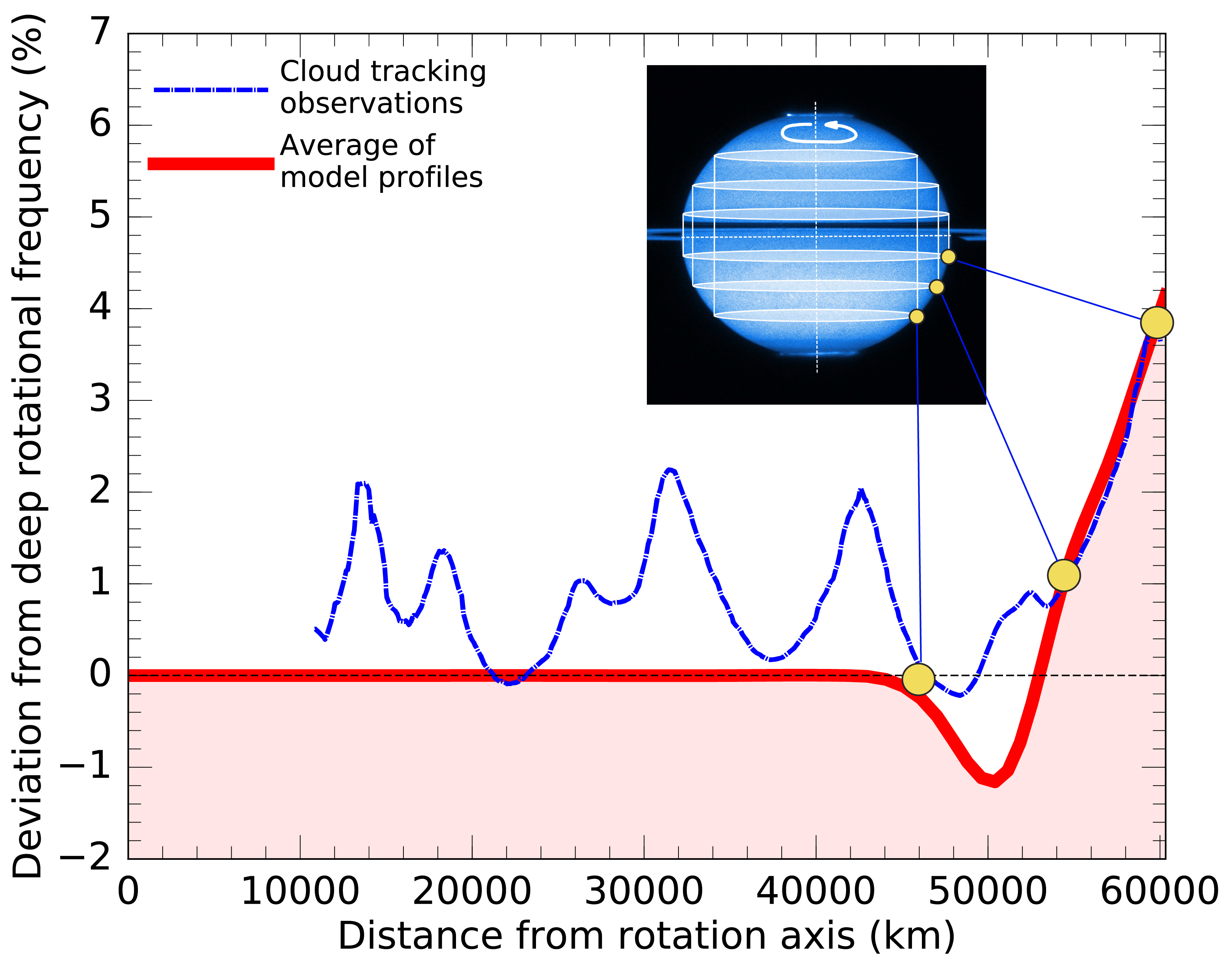
Varying rotation frequency in Saturn's interior.
|
This work is based on a collaborative article published in Science
that is entitled "Measurement and implications of Saturn's gravity
field and ring mass". For everyone to use, here are some slides in PPTX and PDF formats as well four graphics files that I prepared. Robert Sanders prepared this press release. Among the news coverage for this work, this Russian report stood out by explaining we had determined when Saturn became "The Lord of the Rings". Also here is an interview on NPR's radio show Science Friday about this work.
During its 13 years in orbit around Saturn, the Cassini
spacecraft has made a number of remarkable measurements of the planet
and its satellites. But only during its final 22 orbits it dove inside
its rings and measured the planet's gravity fields with unprecedented
precision. Two important findings emerged:
The winds in Saturn's atmosphere are massive and at least 9000 km deep:
We had prepared a suite of
models for Saturn's interior that included different core masses
and amounts of helium
rain. We calculated the expected gravity field and were pretty sure
Saturn's gravity coefficent J8 would fall between -9 and -8
x 10-6. We were completely surprised when the Cassini
spacecraft measured J8 to be -14 x 10-6, which
implied something important was missing from all models that we had
constructed. After we added deep and massive winds to our interior
models we were able to match all gravity coefficients. The winds need
to be at least 9000 km deep. The winds in Saturn atmosphere had been
observed before but no one had assumed they would reach that deep. The
first evidence of very deep winds in giant planets only came late last
year when measurements of the Juno spacecraft predicted the winds on
Jupiter to be between 3000 and 5000 km deep.
Saturn's rings are young and only formed 10-100 million years
ago: When I admired Saturn's spectacular rings, I naively assumed
they were as old as the planet itself (4.5 billion years). The first
gravity measurement of the ring mass now tells us otherwise. They
contain only about 0.4 Mimas masses (2000 Mimas masses = 1 Earth moon)
worth of material, which points to a surprisingly young ring age of only
between 10 and 100 million years. Before that Saturn presumably did
not have any rings. (On our slides,
we explain how one relates ring mass and age.) This tells us a
dramatic event must have occurred near Saturn in our recent solar system
history. 100 million years ago, the dinosaurs still roamed on
Earth. They disappeared when a giant impact occured near the
Yucatan peninsula 65 million years ago. Now we have evidence that a
drastic event occurred near the Saturnian system that produced a gazillion
pieces of icy rubble that make up the rings today. This suggests that our solar system is not such a
stable and happy place as one might think. We assume the rings are
either the leftover debris from a comet that was tidally disrupted by
Saturn's extreme gravity just like the Shoemaker-Levy
comet was pulled apart by Jupiter. Alternatively Saturn originally
had multiple satellites, their orbits become unstable, and it came to a
gigantic collision. We cannot tell which scenario is more likely but we
do know something drastic must have happened in the Saturnian system
fairly recently by astronomical standards.
|
|
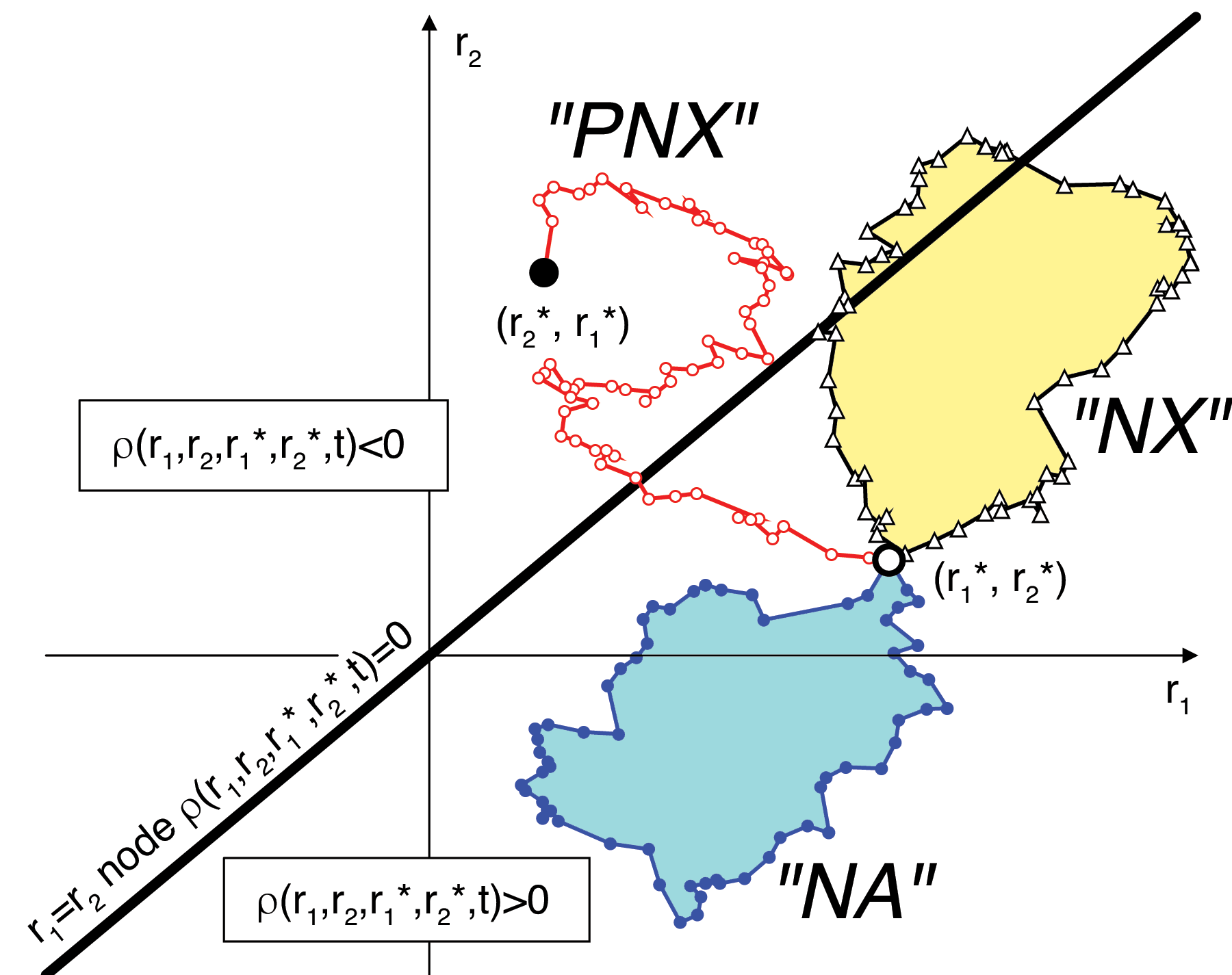
Different paths that enter into PIMC simulations of just two particles. Node-avoiding (NA), node-crossing (NX) as well as permuting, node-crossing (PNX) paths are illustrated. The diagonal black line denotes the node the density matrix, ρ=0.
|
Modeling the behavior of interacting quantum systems on a classical computer is challenging. Here we the Feynman's path integral method to map a system of quantum particles onto a system of classical paths. While most thermodynamic properties can be derived from simulations of closed paths, the computation of the momentum distribution requires open paths. In this article, we compute the momentum distribution of the homogeneous electron gas with path integral Monte Carlo (PIMC) simulations.
Since thsi is a fermionic system, we employed the restricted path approach to deal with the fermion sign problem.
In the restricted PIMC method, only node-avoiding (NA) paths contribute. For two particles, the nodal restriction prohibits all permutations. However, if simulations with the direct fermion method are performed no restrictions are applied. Nonpermuting paths that cross the nodes (NX) and those that avoid it (NA) both enter with a positive sign. Permuting paths (PNX) are now permitted and enter with a negative weight given by the (-1)P factor.
|
|
| |
|
 |
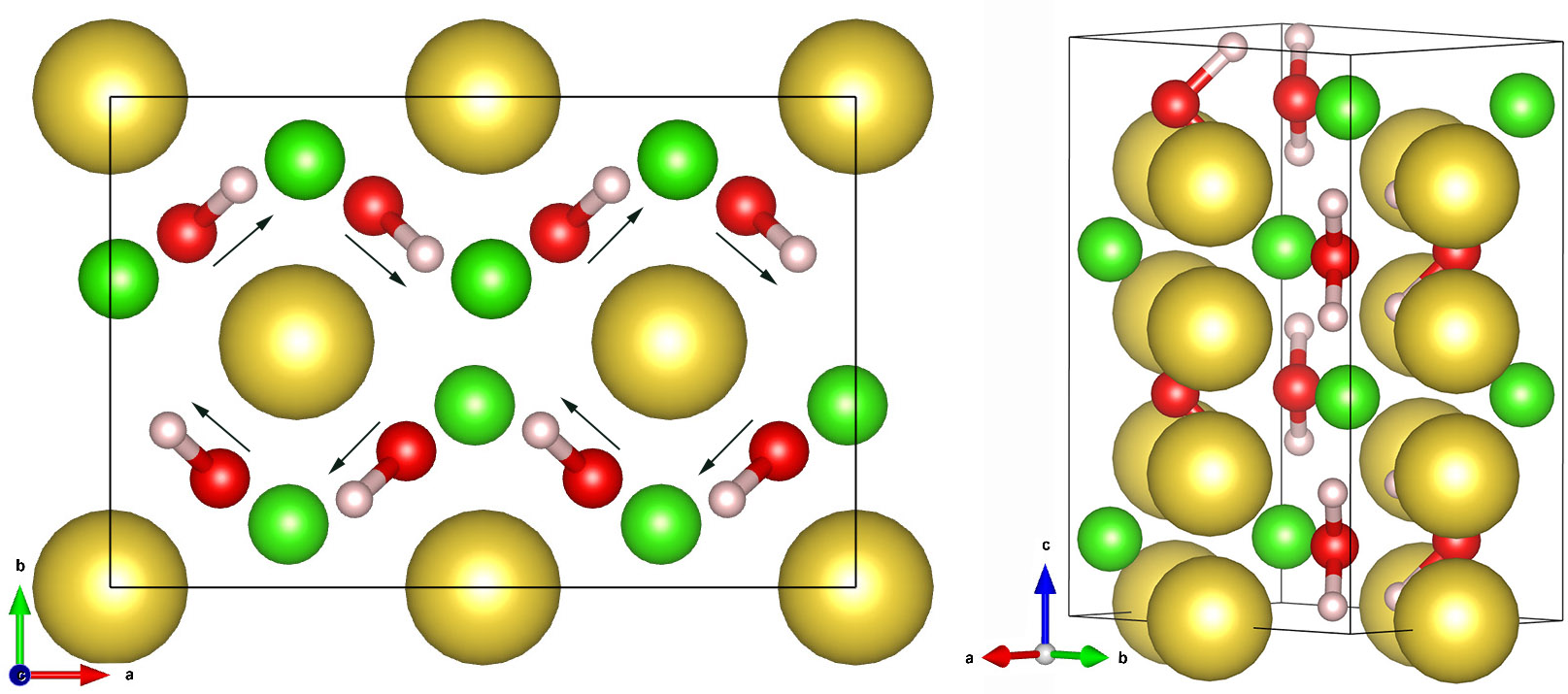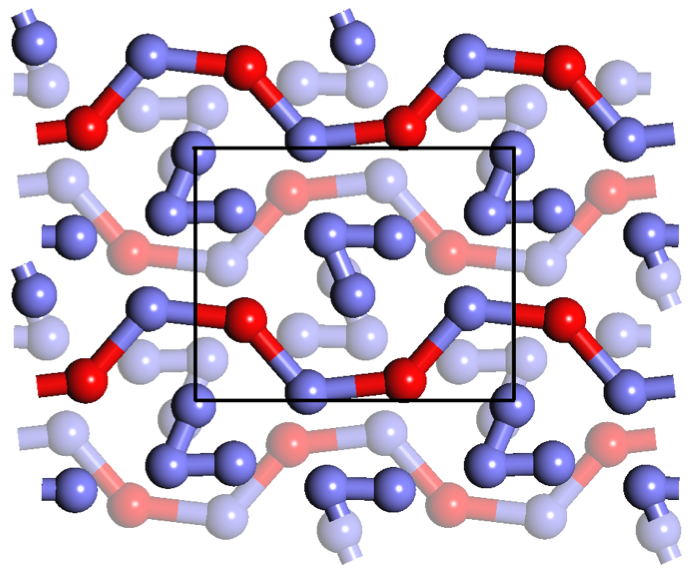
Crystal structure of our new water-salt compound that we predict to form at high pressure. The yellow, green, red, and light spheres denote the positions of the chlorine, sodium, oxygen, and hydrogen atoms. The small arrows denote the dipole of the water molecules that cancel each other out.
|
We developed a new symmetry-driven structure search (SYDSS) algorithm
to predict novel materials with ab initio simulations. In our
recent article, we predict water and
salt form a novel compound at high pressure. While at ambient
conditions, water can only incorporate a modest amount of salt, we
predict that both materials form a novel 1:1 stoichiometric
H2O-NaCl compound at high pressure. It is well-known that
high pressure changes the crystal structure of materials, novel
materials may form, and immiscible compounds can become miscible. In
the same article, we also predict two
unusual carbon oxides, C2O and C4O, to form while
at ambient pressures, only CO2 and CO are known to exist.
| |
|
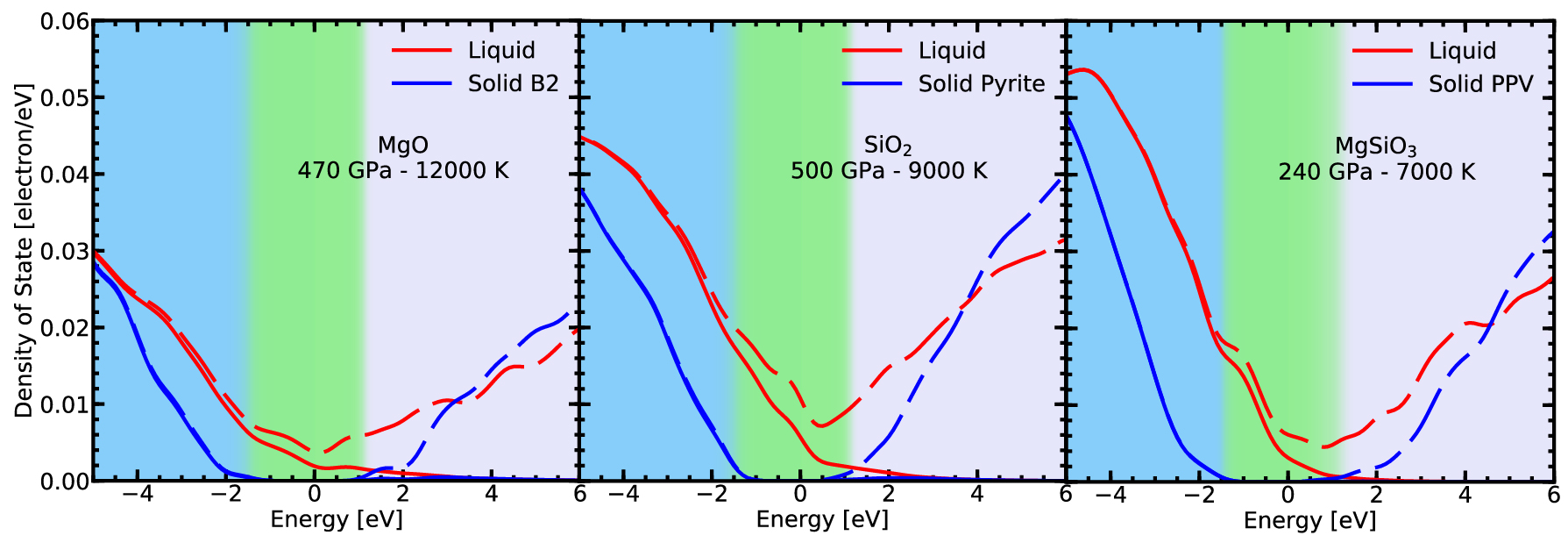
Solid silicates (blue line) are semi-conductors that have excitation gap (green region). Liquid silicates (red line) have no gap and are thus semi-metals. They conduct electricity reasonably well.
|
With the Kepler satellite, thousands of new exoplanets were
discovered. Many of them have been described as Super-Earths since
they are larger than Earth but also have a rocky composition. Their
interiors are much hotter than Earth's and part of their mantles
are likely to be liquid. In our recent article, we
showed that the electrical conductvity of liquid mantles are
sufficiently high so that Super-Earths can generate magnetic fields
with their mantles. This is a new regime for the generation of
planetary magnetic fields. Our magnetic field on Earth is generated in
the liquid outer iron core. On Jupiter, it arises from the convection
of liquid metallic hydrogen. On Uranus and Neptune, it is assumed to
be generated in the ice layers. Now we have added molten rocks to
this diverse list of field generating materials. This also implies
that the magma ocean that existed on the early Earth generated a
magnetic field.
| |
|
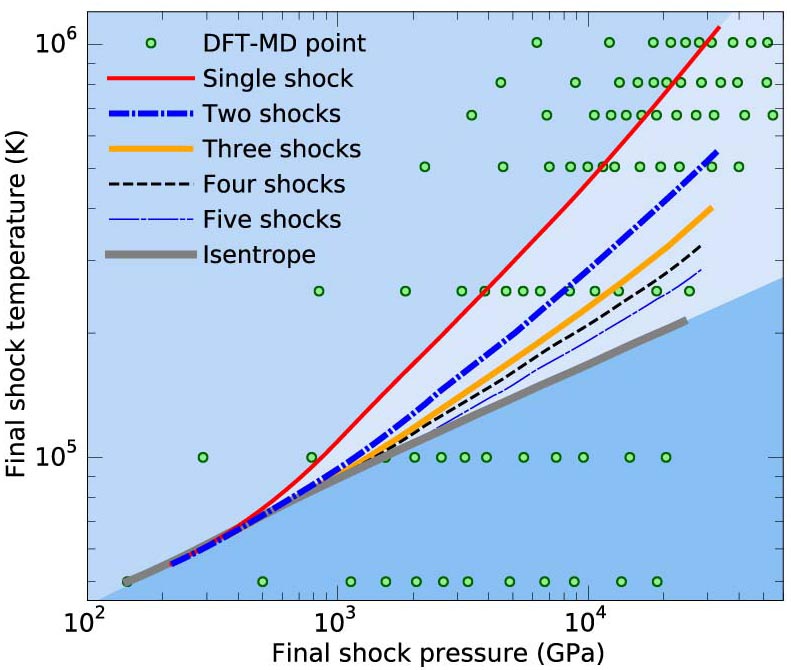
T-P path of experiments with multiple intermediate shocks.
|
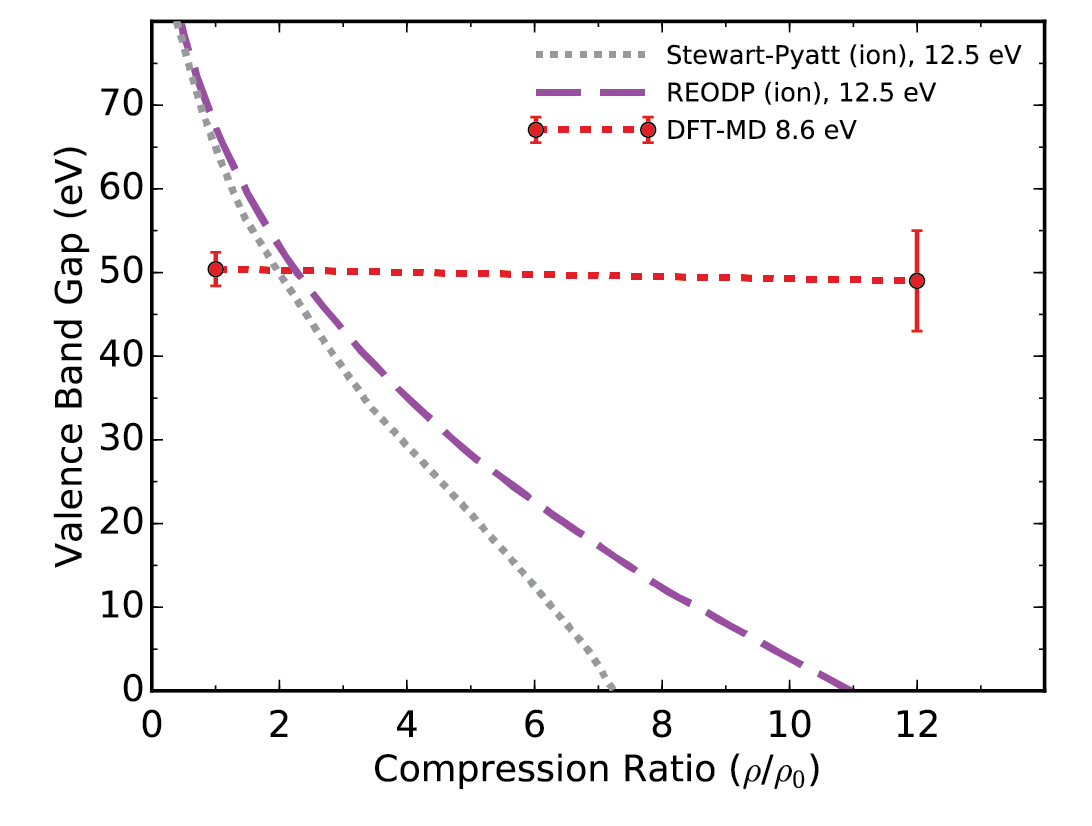
Valence band gap predicted with our DFT-MD simulations and
two semi-analytical models.
|
In our recent article, we studied
aluminum at extreme pressure and temperature conditions with path
integral Monte Carlo and density functional molecular dynamics
simulations. We derive the equation of state and various electronic
properties. In laboratory experiments, one typically uses shock waves
to reach such extreme conditions. The material becomes very hot if just
a single shock is employed. The graph on the left illustrates that
comparatively low, nearly isentropic temperature conditions can be
reached when a number of smaller
shocks are employed instead.
Aluminum is metal. However, there is gap in the electronic density of states between the 2p and the
conduction band. This gap is expected to close at very high density when
the bound 2p state merge with the free particle states. The two
semi-analytical theories (Stewart-Pyatt and REODP) predict the gap to
close rather rapidly with increasing compression. Conversely, with my
DFT-MD simulations, we find the magnitude of the gap hardly changes
up to 12-fold compression. This stark disagreement is subject to
further investigations.
| |
|
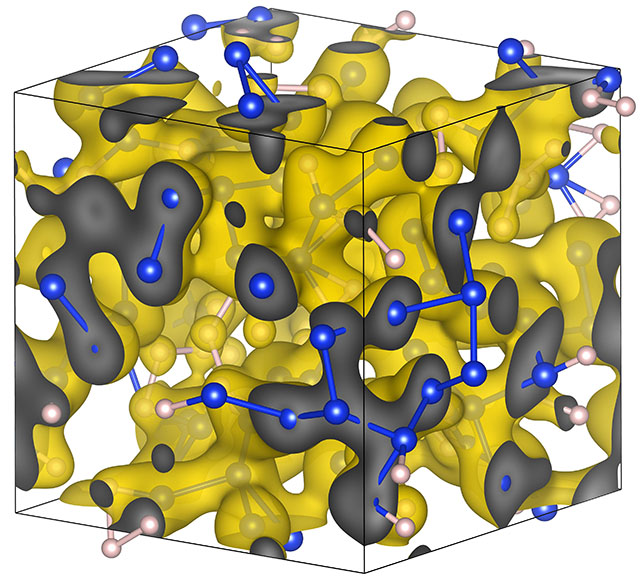
Superionic water in novel P21/c structure.
|
Superionic H2O2 compound.
|
Deep in the interior of Uranus and Neptune, water has been predicted
to occur in a novel, superionic
form. In our latest article, we use
ab initio Gibbs free energy calculations to demonstrate that
superionic water changes from face-centered
cubic form to a novel structure with P21/c symmetry
at 23 Mbar. At even higher pressure of 69 Mbar, superionic water is no
longer stable. It decomposes into two superionic
H2O2 and H9O4 compounds.
|
|
Polymeric CH structure at high pressure and temperature. The blue and white spheres denote the C and H atoms, respectively. The yellow isosurface denotes the electron density.
|
| 
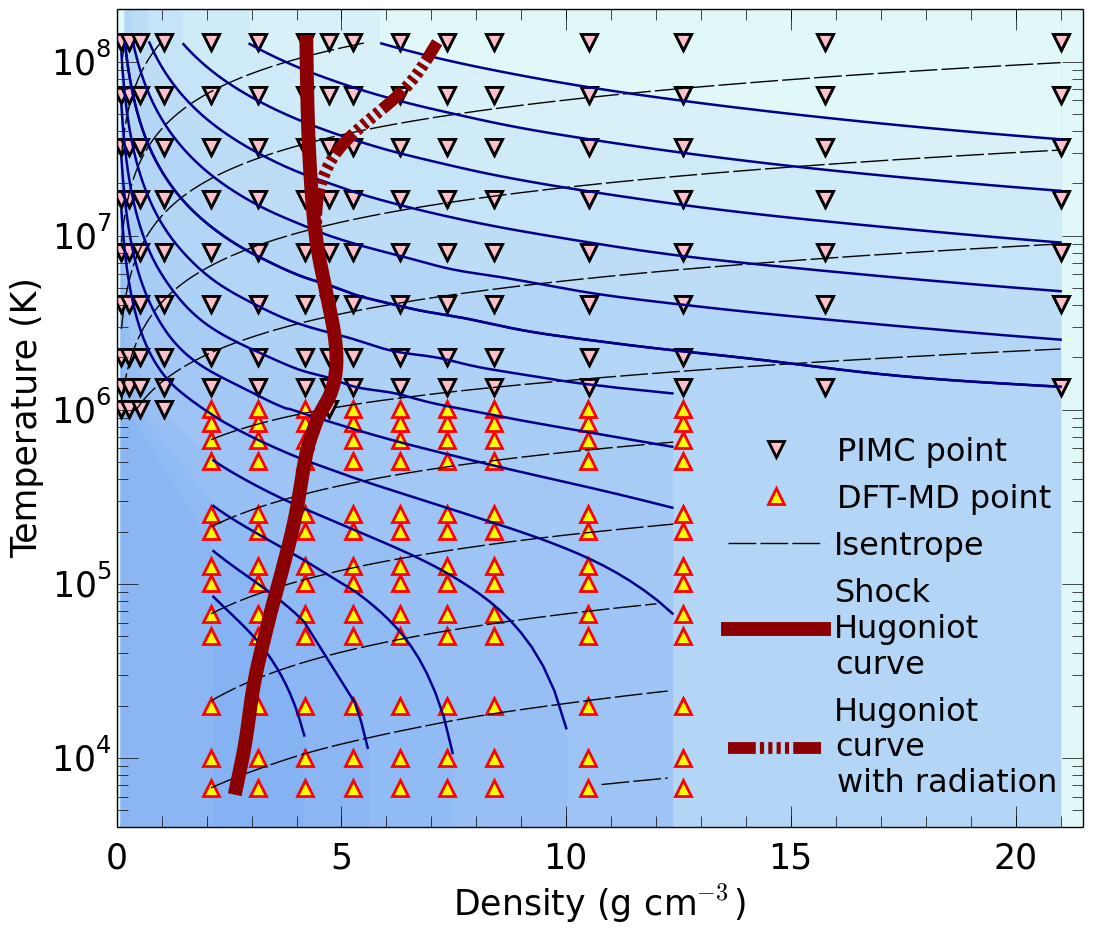Density-temperature conditions of our simulations. The black and red triangles label our PIMC and DFT-MD simulations, respectively.
|
|
In these two articles, (a)
and (b), we investigate CH
pastic materials at extreme pressure-temperature conditions that are
relevant to inertial confinement fusion experiments. Such hydrocarbon
plasmas are of broad interest to laser shock experimentalists, high
energy density physicists, and astrophysicists. Our project has been
support by a Bluewaters computer
time allocation.
|
|
|
|
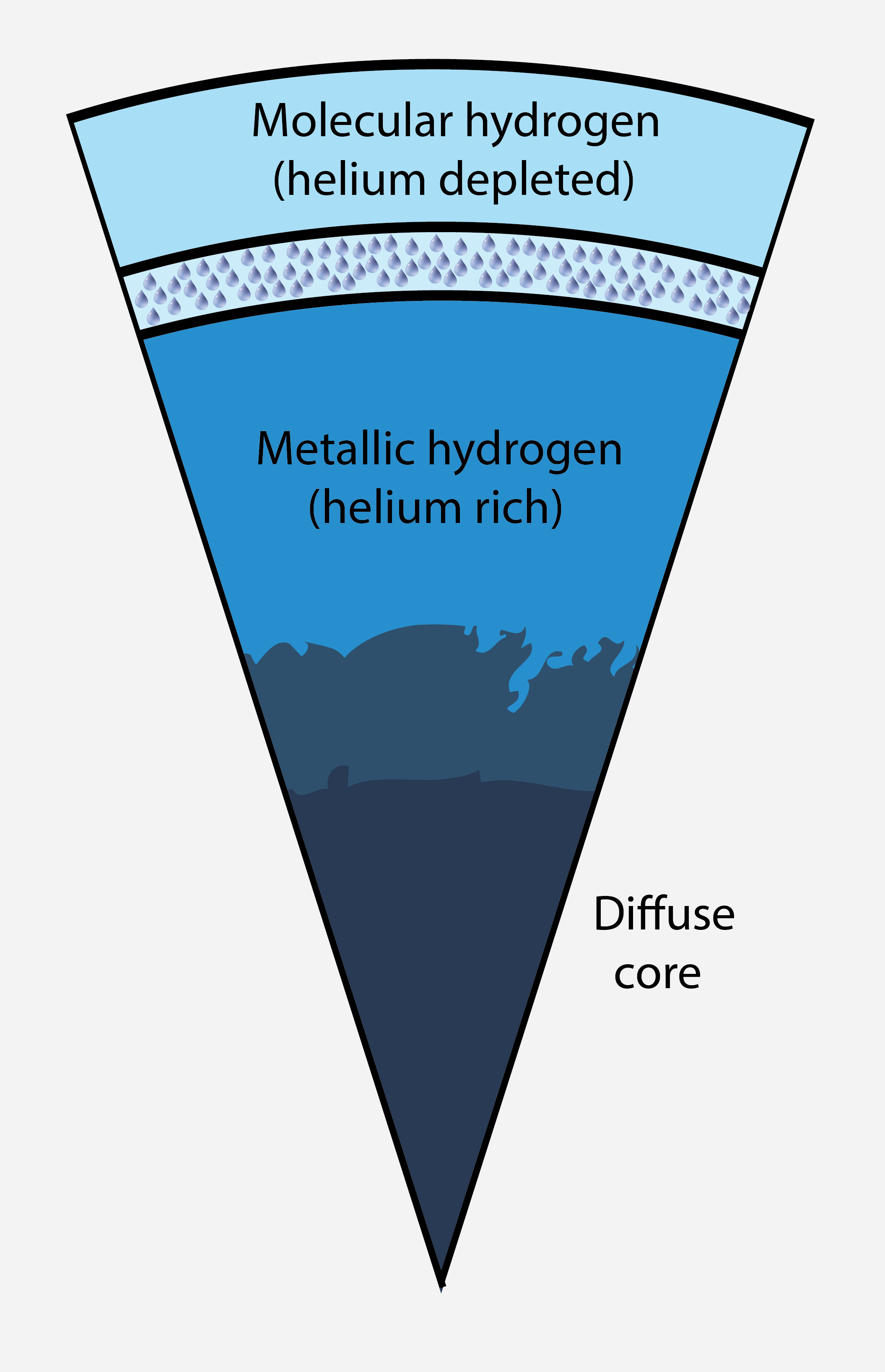
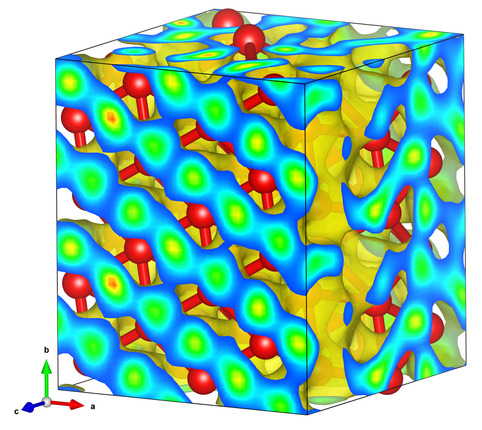
Jupiter interior model with a dilute core.
|
Most models for Jupiter's formation assume it started with a dense
core of rock and ice. Once that reached a critical mass of ~10 Earth
masses, the run-away accretion of hydrogen-helium gas set in, which
lasted until Jupiter had consumed all the gas in its vicinity,
leading to a giant planet of 318 Earth masses.
While the temperature and pressure conditions in the planet's center
reached ~16000 K and ~40 Mbar, the fate of the core remains
ill-understood. Typical core materials like water ice, MgO, SiO2, and iron are all
soluable in hydrogen, which assumes a metallic state under these
extreme conditions. It is not unclear, however, if there was
sufficent convective energy in Jupiter's early history to spread out
the heavy core materials against the forces of gravity.
Here we construct a series of models for Jupiter's interior in
order to match the recent gravity measurments of the Juno
spacecraft. We demonstrate models with a dilute core match the
observations better lending support to the hypothesis that heavy
material in Jupiter's core have been redistributed over a
substantial fraction of the planet's radius. Different terms ranging
diffuse, dilute, expanded and even fuzzy have been invoked to
describe such a core. A Jupiter model with a dilute core is shown on the left.
|
|
|
|
Calcite I crystal structure. The blue, brown, and red spheres denote the Ca, C and O ions respectively. The red isosurface denotes the electron density.
|
| 
Calcite V propeller phase. The yellow isosurface denotes the density of oxygen ions that emerges from the propeller rotation of the carbonate CO32- ions.
|
With ab initio computer simulations, we studied the unusual
propeller motion of the carbonate CO32- ions in
phase V of calcite (CaCO3). We found that the ions
perform a tumbling motion and instead of rotating like a perfectly
mounted propeller. We also demonstrated that this phase is denser than
the liquid implying a negative slope of the melting line.
|
|
|
|
Computer simulation of a hot, dense mixture of hydrogen (white), helium (green) and iron (yellow spheres) atoms.
|
Giant planets are primarily composed of hydrogen and helium but they
also contain a small amount of heavier elements. In the atmosphere
they make up less than 3% by mass but they dominate the planets
opacity. Without their presence we would be able to see through
Jupiter's molecular layer and directly observe the planet's metallic
interior where its magnetic field is generated. Most scientists
assume Jupiter has a core composed of heavy elements. Its size and
composition is uncertain but we estimated its mass to be worth 12
Earth
masses. The
total heavy element fraction in the planet could be as high as
7%.
In
this article, Francois Soubiran investigates the properties of
various heavy elements in giant planet interiors. The equation of
state is computed for C, N, O, Si, Fe, MgO and SiO2 mixed
with hydrogen and helium. Effective mixing rules are derived to make
models of giant planet interiors more accurate.
|
|
|
|
|
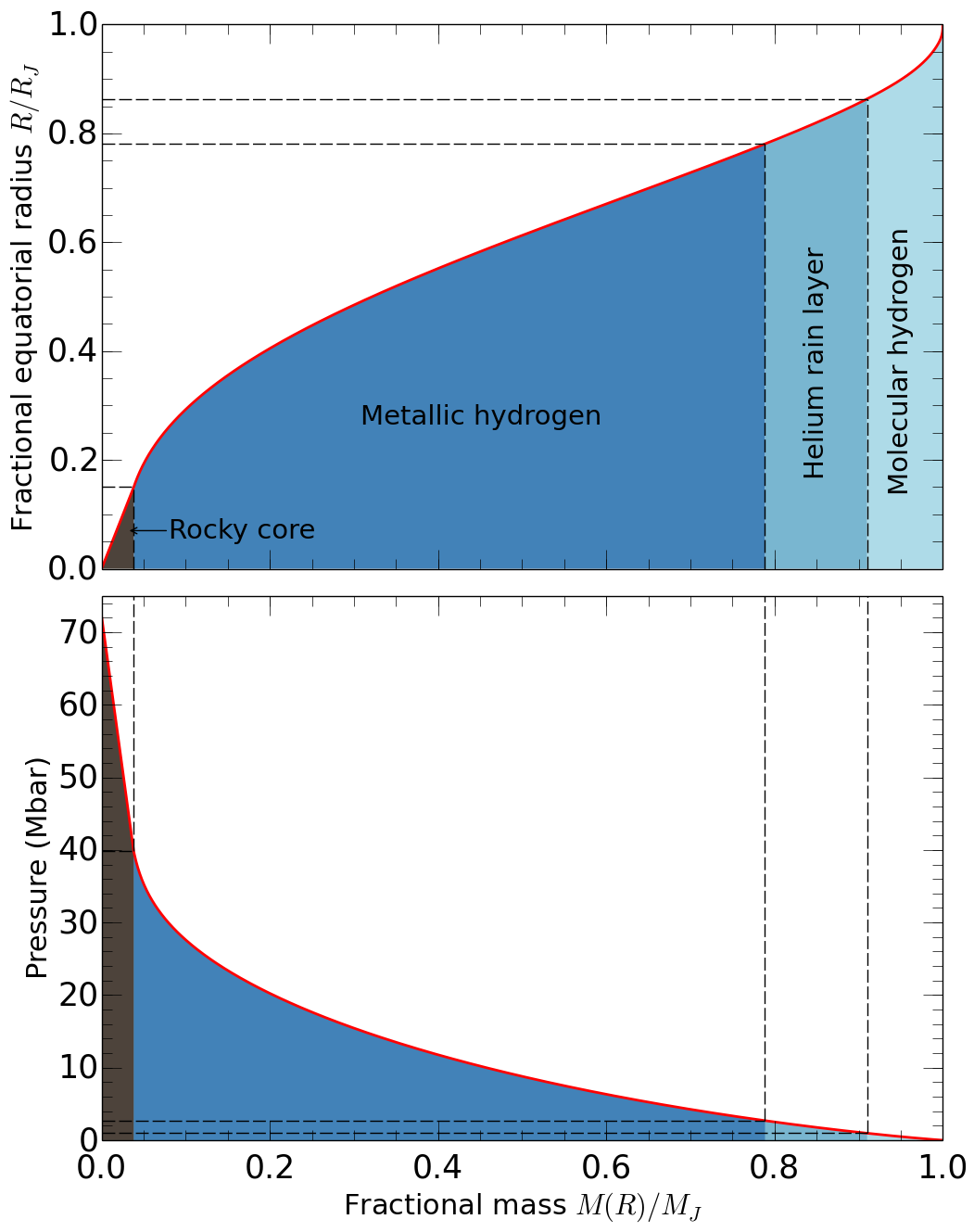
This article provides an overview of how models of giant planet
interiors are constructed. We review measurements from past space
missions that provide constraints for the interior structure of
Jupiter. We discuss typical three-layer interior models that consist
of a dense central core and an inner metallic and an outer molecular
hydrogen-helium layer. These models rely heavily on experiments,
analytical theory, and first-principle computer simulations of
hydrogen and helium to understand their behavior up to the extreme
pressures ~10 Mbar and temperatures ~10,000 K. We
review the various equations of state used in Jupiter models and
compare them with shock wave experiments. We discuss the possibility
of helium rain, core erosion and double diffusive convection may
have important consequences for the structure and evolution of giant
planets.
The diagram on the left shows the radius and fractional mass as function of mass for a typical model. The color label various layers.
|
|
|
|
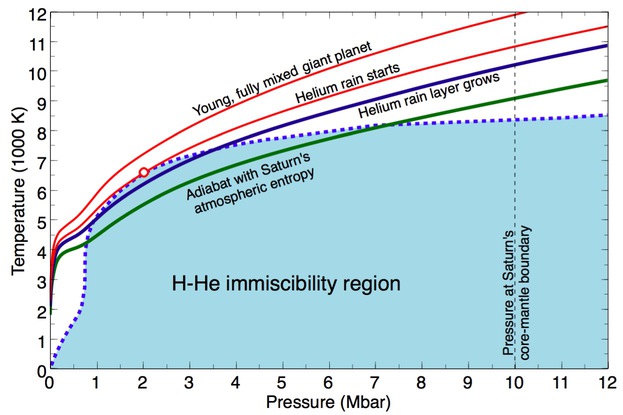Temperature-pressure profiles for Jupiter's interior during the planet's evolution.
|
When the Juno
spacecraft arrives at Jupiter in July of this year, it will map
out the planet's gravity field with unprecedented precision. What can
we expect to learn about Jupiter's interior? Based on earlier
measurements and on results from ab initio computer simulations
of mixtures of hydrogen, helium, and some heavier elements, Bill Hubbard
and I put together a number of different interior models (ApJ, 2016)
. We predict a massive core of 12 Earth masses consistent with earlier models. Furthermore, we
predict that helium rain
has occurred on this planet for some time, which is a direct
consequence of combining the measurements of the Galileo
entry probe with results from ab initio calculations for
the hydrogen-helium immiscibility
and adiabats.
|
|
|
|
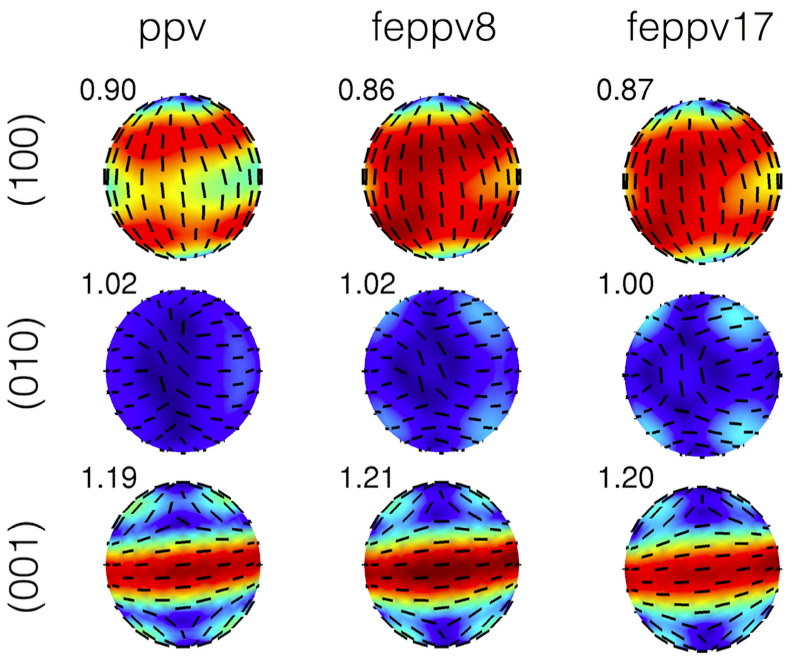
Shear wave splitting strength.
|
Despite a wealth of seismic observations, many questions about the
compositions of the Earth's mantle have remained unanswered. In a
recent study (EPSL, 2016) lead by Shuai Zhang, we show that
the assumption of a pyrolitic composition for the deep Earth is in
good agreement with the preliminary reference Earth model (PREM), which is
a 1D seismological representation of the Earth's interior. In collaboration with
Tao Liu and Stephen Stackhouse (Leeds U.) and Sanne Cottaar (Cambridge
U.), we performed ab initio molecular dynamics to calculate the
elastic and seismic properties of pure, Fe3+ and
Fe2+, and Al3+ bearing MgSiO3
perovskite and post-perovskite over a wide range of pressures,
temperatures, and Fe/Al compositions.
|
|
|
|
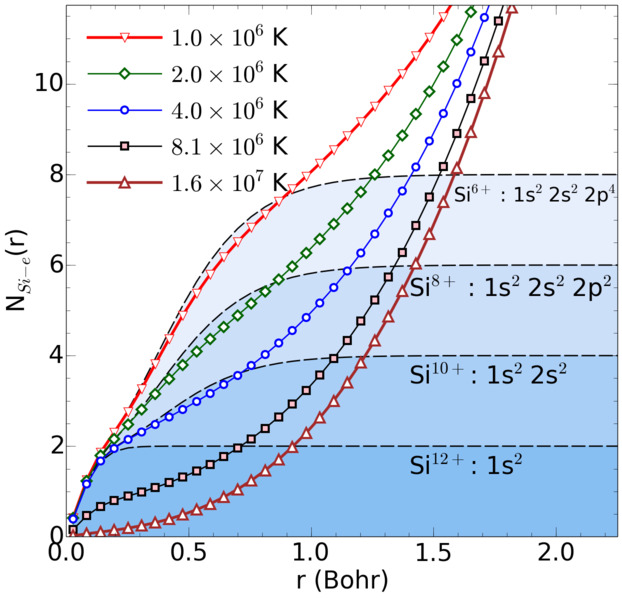Nucleus-electron correlation functions.
|
In our recent publication in Physical
Review Letters, Kevin Driver and I extended the applicability range of
fermionic path integral Monte Carlo simulations to heavier elements
and lower temperatures by introducing various localized nodal
surfaces. Hartree-Fock nodes yield the most accurate prediction
for pressure and internal energy that we combine with the results from
density functional molecular dynamics simulations to obtain a
consistent equation of state for hot, dense silicon under plasma
conditions and in the regime of warm dense matter (2.3-18.6 g/cc,
5x105 - 1.3x108K). The shock Hugoniot curve is
derived and the structure of the fluid is characterized with pair
correlation functions. On the left, we estimate the degree of
ionization by comparing the integrated nucleus-electron pair
correlation functions from PIMC (symbols) with results for isolated
atoms (black dashed lines).
|
|
|
|
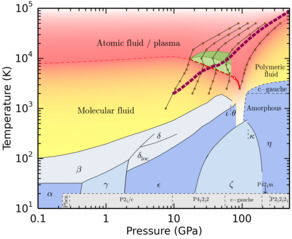
Phase diagram of nitrogen.
|
In two articles, Kevin Driver, Francois Soubiran, Shuai Zhang, and I
combine path integral Monte Carlo simulations and density functional
molecular dynamics to study oxygen
and nitrogen
in the regime of warm dense matter. We characterize both material at
extreme pressure and temperature conditions that exist in stellar
interiors and can be probed with shock wave experiments. We use pair
correlation functions and the electronic density of states to describe
changes in the structure of the plasma. We compute the shock Hugoniot
curves to compare with laboratory experiments. For nitrogen, we
characterize the regime of molecular dissociation that leads to a
region of dP/dT<0 at high pressure, which is shown in green in the
phase diagram on the left.
|
|
|
|
Simulation of a H2-H2O mixture.
|
Ice giant planets are typically assumed to have a hydrogen-rich
atmosphere, an intermediate ice layer, and a rocky core. Such
three-layer models satisfy the observational constraints for Uranus
and Neptune. However, it remains unclear whether these planets have
oceans, which would imply the existence of a sharp boundary
between the hydrogen and water layers. Alternatively, the density and
the water contents of the atmosphere could increase gradually. Recent
laboratory experiments by Bali at el. (2013) favored the ocean
hypothesis. In our ApJ
article, Francois Soubiran and I used ab initio computer
simulations to determine whether H2 and H2O are
missible at high pressure. Contrary to the experimental predictions,
we find that both materials are fully miscible under ice giant
interior conditions. We predict that these planets can only have
oceans if icy building blocks were delivered before the gas was
accreted during planet formation.
|
|
|
|
Simulation of a liquid iron-MgO mixture. The brown,
green, and red spheres denote Fe, Mg, and O atoms. The grey surfaces
show the electron density.
|
All known terrestrial planets have a separate iron core and a rocky
mantle because metallic iron has a low solubility in rocky materials
under typical pressure-temperature conditions in the planetary
interiors. However, at sufficiently high temperatures, all materials
eventually become miscible, even oil and water.
In our recent article,
Sean Wahl and I use ab initio computer simulations to
determine what temperature would be required for iron and MgO to
become miscible in all proportions. We find that the required
temperature rises from 4000 to 10,000 K as the pressure is increased
from 0 to 500 GPa. Such extreme conditions can be reached during a
giant impact on a terrestral planet, implying that not all iron would
settle into core during such an event.
|
|
|
|
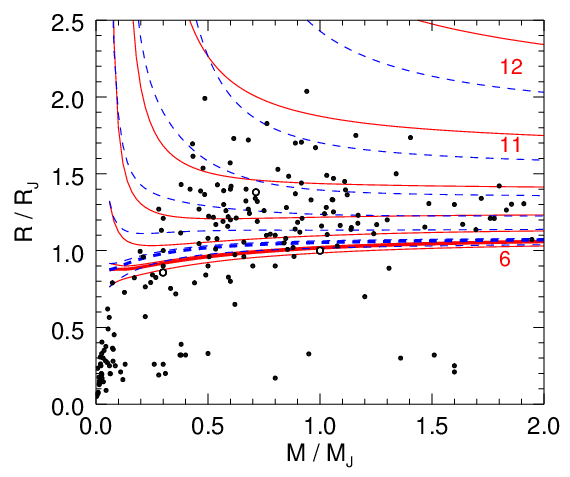Revised mass-radius relation
for giant exoplanets. Our new simulation data are shown in red.
|
Using density functional molecular dynamics simulations, we determine
the equation of state for hydrogen-helium mixtures spanning
density-temperature conditions typical of giant planet interiors. In
our manuscript, a comprehensive equation
of state table with 391 density-temperature points is
constructed and the results are presented in form of two-dimensional
free energy fit for interpolation.
We present a revision to the
mass-radius relationship which makes the hottest exoplanets increase
in radius by ~0.2 Jupiter radii at fixed entropy and for masses
greater than ~0.5 Jupiter mass. This change is large enough to
have possible implications for some discrepant "inflated giant
exoplanets".
Our full EOS table as well as our free energy interpolation code has just been made available here.
|
|
|
|
|
In the interiors of Uranus and Neptune (dashed lines in the left
figure), water is predicted to occur in a superionic state where the
oxgyen atoms remain stationary like in a solid while the hydrogen
atoms diffuse throughout the crystal like a fluid. Here, we
show that, at 1.0±0.5 Mbar, the oxygen sub-lattice in superionic
water changes from a body-centered cubic lattice (middle) to an
face-cented cubic lattice (right). This transformation lead to a more
efficient packing but also reduces the hydrogen diffusion rate, which
may have further implications for electronic conductivity and magnetic
dynamo in Uranus and Neptune. Our results were highlighted by Phys.org
|
|
|
Oxygen (red) and hydrogen (blue) atoms in the new H4O structure.
|
Water and hydrogen at high pressure make up a substantial fraction of
the interiors of giant planets. Using ab initio random
structure search methods we investigate the ground-state crystal
structures of water, hydrogen, and hydrogen-oxygen compounds. Here, we find that, at pressures
beyond 14 Mbar, excess hydrogen is incorporated into the ice phase to
form a novel structure with H4O stoichiometry.
We also
predict two new ground state structures of water ice with P21/m
and I4/mmm symmetry to form at 135 and 330 Mbar,
respectively. Here is a slide that summarizes the
seven new high pressure ice phases that were recently predicted with
ab initio calculations.
|
|
|
|
 |
|
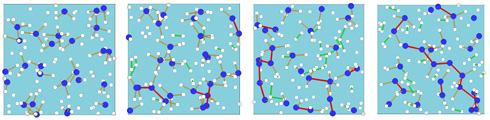
The four snapshots from our ab initio simulations show how
methane gas at high pressure and temperature forms long hydrocarbon
chains. The blue and white spheres denotes the carbon (C) and hydrogen
atoms, respectively. The red lines indicate the C-C bonds that
increase from left to right. In our recent paper, we show that the resulting
polymeric state is metallic and exists in the interiors of Uranus and
Neptune. We also predict how such a transformation on the atomistic
level can be identified with macroscopic shock wave experiments.
|
|
|
|
|
Path integral Monte Carlo simulations are a powerful tool to study
quantum systems at high temperature but applications to elements
beyond hydrogen and helium with core electrons have so far not been possible. In
our recent PRL
article, Kevin Driver and I develop a new all-electron path integral Monte Carlo
technique with free-particle nodes for warm dense matter and apply it
to water and carbon plasmas. Our results for pressures, internal
energies, and pair correlation functions compare well with density
functional molecular dynamics at temperatures of
(2.5-7.5)·105K. Both methods together form a coherent
equation of state over a density-temperature range of 3-12 g/cc and 104-109 K.
|
|
|
|
|
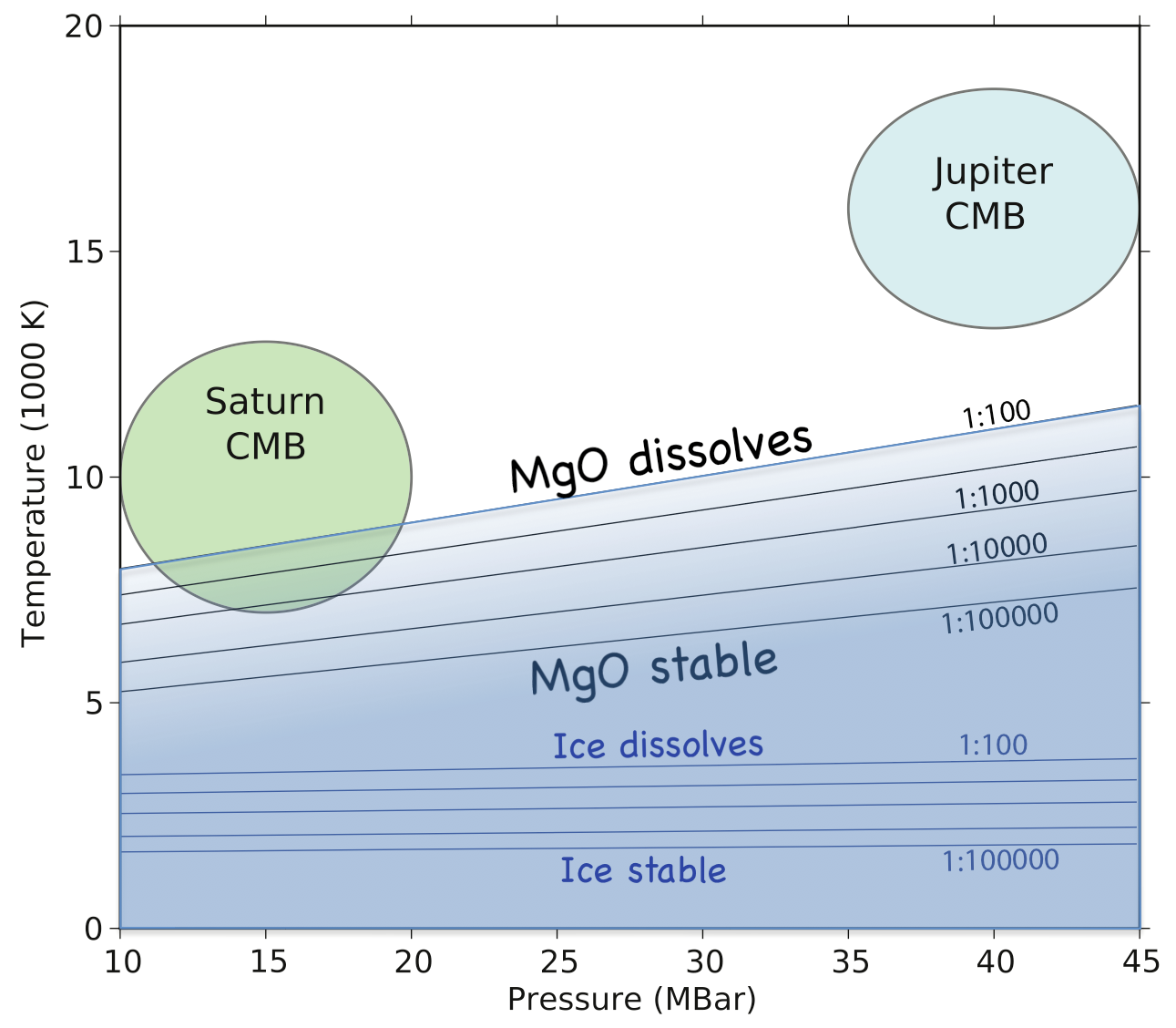
Gas giants are believed to form by the accretion of hydrogen-helium
gas around an initial protocore of rock and ice. The question of
whether the rocky parts of the core dissolve into the layer of
metallic fluid hydrogen following formation has significant
implications for planetary structure and evolution. Here we use ab initio
calculations to study rock solubility in fluid hydrogen, choosing
magnesium oxide as a representative example of planetary rocky
materials, and find MgO to be highly soluble in H for temperatures in
excess of approximately 10000 K, implying significant redistribution
of rocky core material in Jupiter and larger exoplanets.
|
|
|
|
|
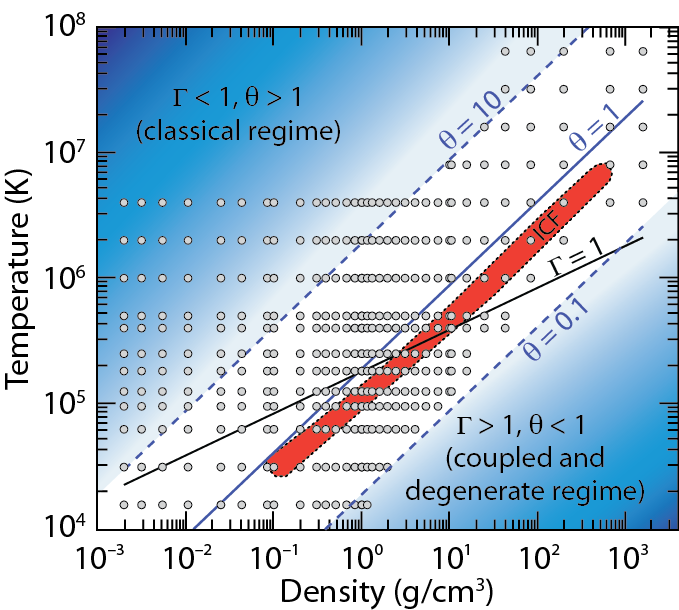
Using path integral Monte Carlo simulations we have derived an
equation of state (EOS) table for deuterium that covers typical intertial
confinement fusion conditions at densities ranging from 0.002 to 1596
g/cm3
and temperatures of 1.35 eV ~ 5.5 keV. The small grey circles in the
diagram on the left indicate the temperature-density conditions of our
simulations. The EOS and related results are summarized in an article that has been published in Physical Review B.
|
|
|
|
|
The bonding properties of water ice at high pressure are studied in this article. By comparing the Wannier orbitals in the Pnma structure (shown in the image on the left), one can tell that they differ substantially from the sp3
hybridization in the ice X phase at lower pressures. Most strikingly,
the white orbitals are not aligned with any hydrogen bond.
|
|
|
|
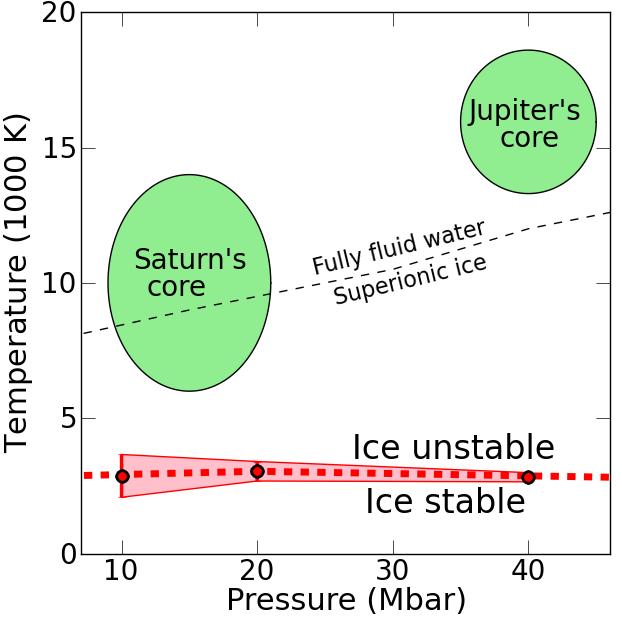
Simulations predict water ice to be unstable above 3000 Kelvin when exposed to metallic hydrogen
|
The four giant planets in our solar system grow so large because icy
comets made their cores grow much faster than those of terrestrial
planets, which enabled them to accrete large amounts of gas. With ab
initio simulations, Hugh Wilson and I demonstrate in our recent manuscript
that water ice is not thermodynamically stable at the temperature and
pressure conditions where core is exposed to the layer of metallic
hydrogen above. This implies that the cores in Jupiter and Saturn have
been eroded over time, with the icy material being redistributed
convectively throughout the planet.
Our work has implications for constraining the interior
structure and evolution of giant planets and will be relevant for the
interpretation of data from NASA's Juno mission to Jupiter (to be launched in
August 2011). Core erosion could also provide a significant flux of
heavy elements to the atmosphere of exoplanets and may explain why
some of them have significantly inflated radii.
|
|
|
|
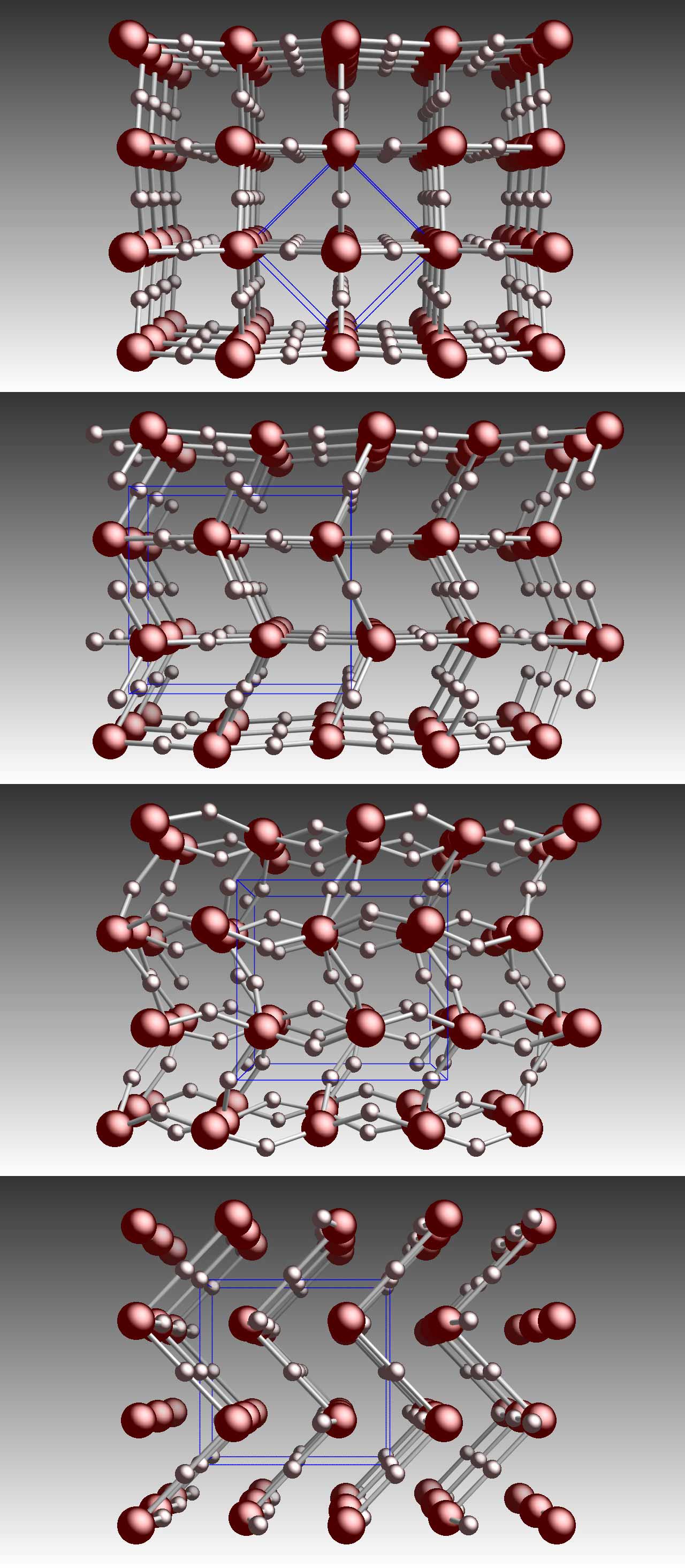
Four high pressure phases of ice
|
Water ice is one of the most prevalent substances in the solar system,
with the majority of it existing at high pressures in the interiors of
giant planets. The known phase diagram of water is extremely rich, with
at least fifteen crystal phases observed experimentally. In our article in Physical Review Letters (see
also cond-mat), Hugh
Wilson and I explore the phase diagram of water ice by means of ab
initio computer simulations and predict two
new phases to occur at megabar pressures. In the figure from
top to bottom, you see
1) ice X the highest pressure phase seen in experiments,
2) the Pbcm phase that was predicted with computer simulations in 1996,
3) our new Pbca phase that transforms out of the Pbcm
phase via a phonon instability at 7.6 Mbar, and finally
4) our new Cmcm structure that is
metallic and predicted to occur at 15.5 Mbar.
The known high pressure ice phases VII, VIII, X and Pbcm as
well as our Pbca phase are all insulating and composed of two
interpenetrating hydrogen bonded networks, but the Cmcm
structure is metallic and consists of corrugated sheets of H and O
atoms. The H atoms are squeezed into octahedral positions between
next-nearest O atoms while they occupy tetrahedral positions between
nearest O atoms in the ice X, Pbcm, and Pbca phases.
|
|
|
|
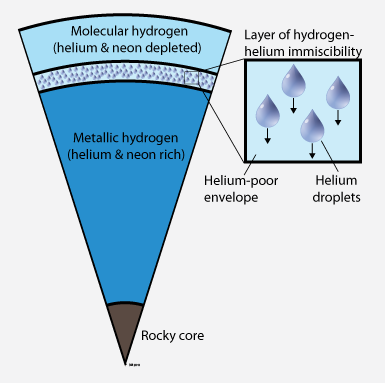
Jupiter’s interior. Helium rain occurs in the immiscibility layer and depletes the upper layer of both helium and neon.
|
When the Galileo entry
probe entered Jupiter's atmosphere in 1995, it measured that
the inert gas neon was depleted by a
factor of 10 compared to the composition of sun, which represents the
concentrations in nebula that formed our solar system with all its
eight planets. So where is all the neon gone that was present in
Jupiter initially? Using ab initio computer
simulations Hugh Wilson and I link the missing neon to another
process that was proposed to occur inside Jupiter: helium
rain.
There is indirect evidence from luminosity measurements that helium
rain occurs on Saturn but it was unclear whether it occurs inside
Jupiter also. Our calculations now show that neon preferentially
dissolves into helium droplets and it is therefore gradually sequestered
into the deeper interior as the helium rain falls. The remaining hydrogen-rich envelope is
slowly depleted of both neon and helium. The measured concentrations
of both elements agree quantitatively with our calculations.
Read commentary by J. Fortney "Peering into Jupiter", UC Berkeley's press release, Discovery Channel and LA Times articles.
|
|
|
|
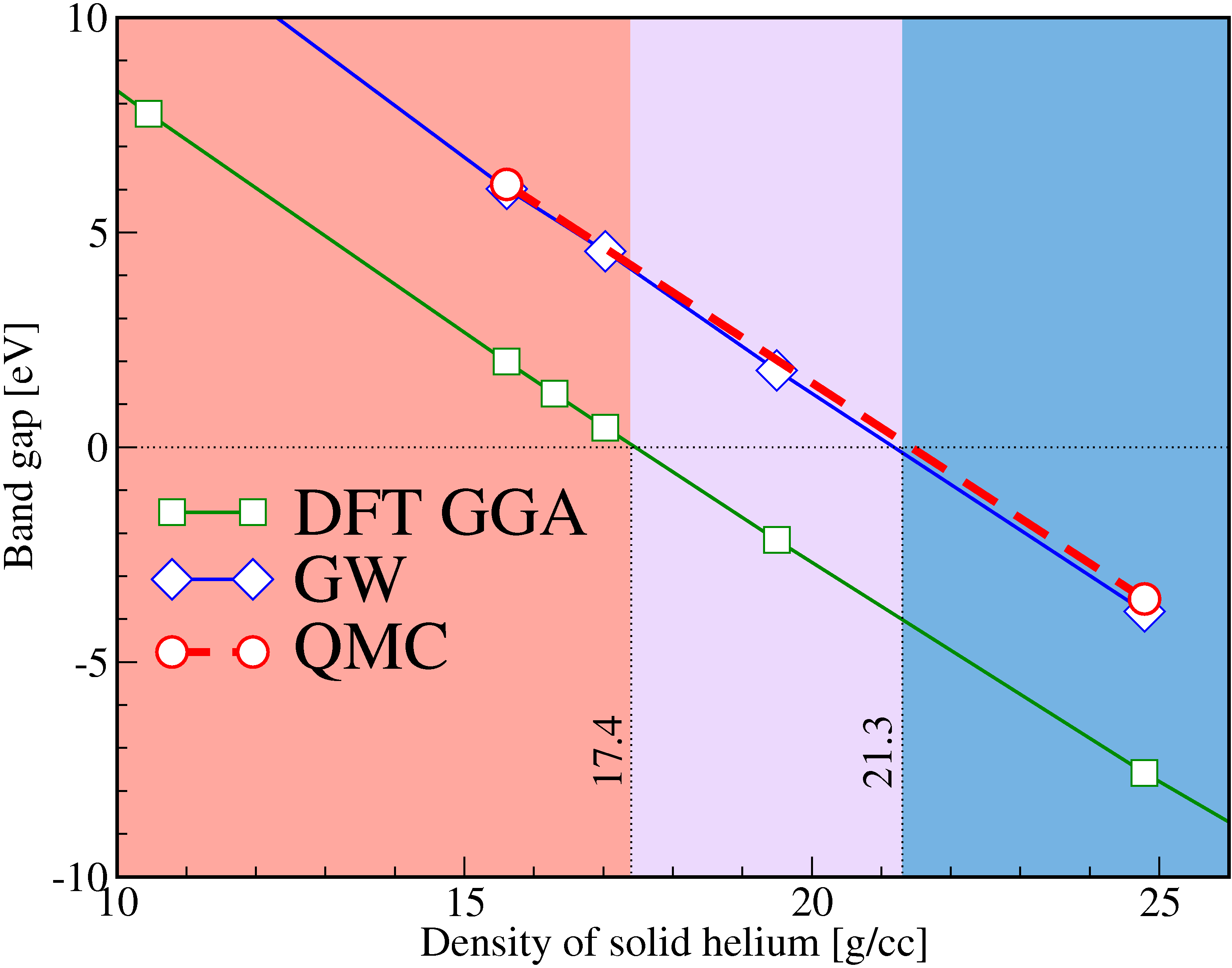
Insulator-to-Metal Transition in Solid Helium at High Pressure
|
Metallic solid helium is present in the outer layers of White Dwarf
stars. The cooling rate of White Dwarfs is regulated by the heat flow
from the hot interior to the colder exterior. The
insulator-to-metal transition is of interest because it marks the
point where heat transport switches from electronic
conductions to photon diffusion. In our paper, the
insulator-to-metal transition in solid helium at high pressure is
studied with different first-principles simulations. Diffusion quantum
Monte Carlo (QMC) calculations predict that the band gap closes at a
density of 21.3 g/cc and a pressure of 25.7 terapascals, which is 20%
higher in density and 40 higher in pressure than predicted by standard
density functional calculations. The metallization density derived
from GW calculations is found to be in very close agreement with QMC
predictions. Path integral Monte Carlo calculations showed that
the zero-point motion of the nuclei has no significant effect on the
metallization transition.
|
| |
|
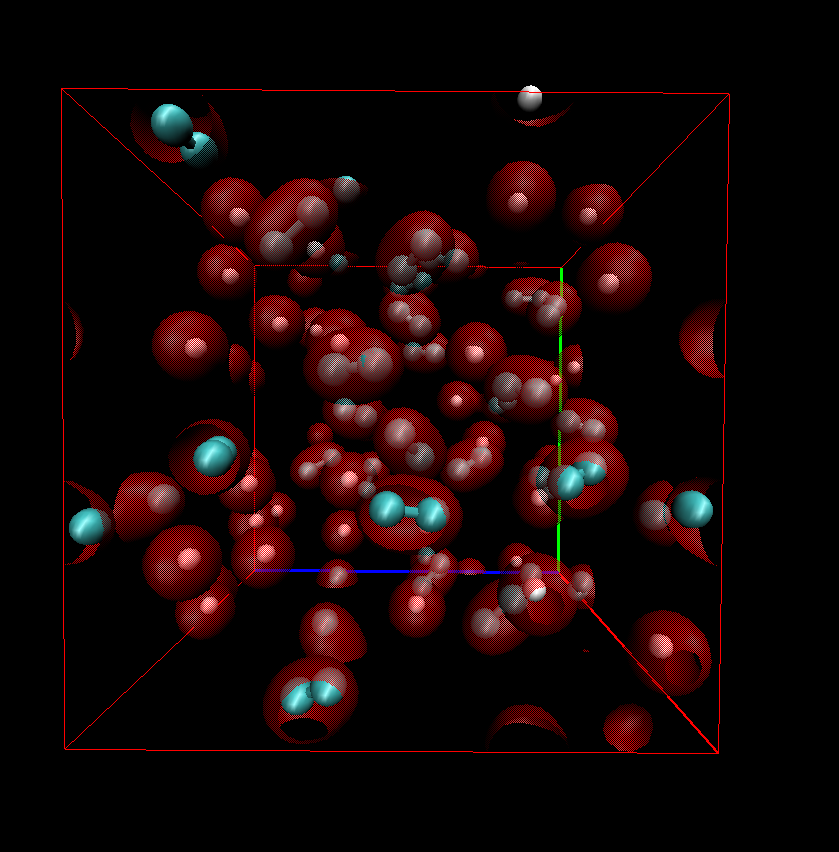
Helium in molecular hydrogen
|
Helium in metallic hydrogen
|
We performed density functional molecular dynamics simulation to
characterize hydrogen-helium mixtures in the interior of solar and
extrasolar giant planets. In this
article, we address outstanding questions about their structure
and evolution e.g. whether Jupiter has a rocky core and if it was
formed by a core accretion process. We describe how the presence of
helium defers the molecular-to-metallic transition in hydrogen to
higher pressures by stabilizing hydrogen molecules.
| |
|
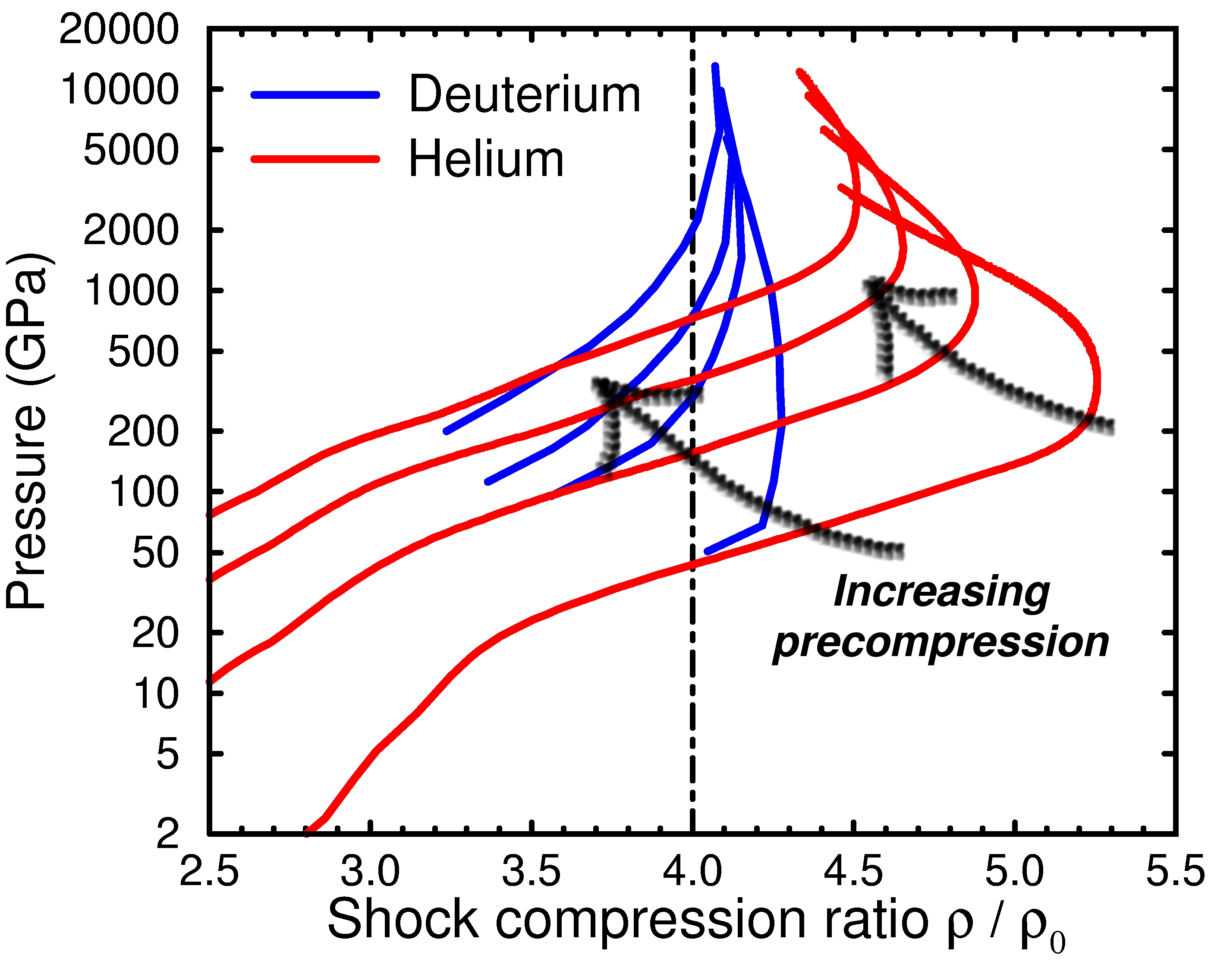
Shock hugoniot curves for precompressed hydrogen and helium.
|
Shock wave experiments allow one to study a material's properties at
high pressure and temperature. In this
article, we
used first-principles computer simulation to predict the properties of
shock fluid helium at megabar pressures. The simulations show that the
compressibility of helium is substantially increased by electronic
excitations. A maximum compression ratio of 5.24-fold the initial
density was predicted for 360 GPa and 150000 K. This result
distinguishes helium from deuterium, for which simulations predicted a
maximum compression ratio of 4.3. If the sample are precompressed
statically the compression ratio is reduced, which is shown in the
left graph.
|
| |
|
Spin fluctuations present molecular oxygen (left) are suppressed at high pressures (right).
|
In recent shock wave experiments [Phys. Rev. Lett. 86, 3108 (2001)],
the conductivity of liquid oxygen was measured for pressures up to 1.8
Mbar and indications for a insulator-metal transition were found.
In this article, we report
results from density functional molecular dynamics simulations of dense liquid oxygen
close to the metal-insulator transition. We have
found that band gap closure occurs in the molecular liquid, with a
slow transition from a semi-conducting to a poor metallic state
occurring over a wide pressure range. At approximately 80 GPa,
molecular dissociation is observed in the metallic fluid. Spin
fluctuations play a key role in determining the electronic structure
of the low pressure fluid, while they are suppressed at high pressure.
|
| |
|
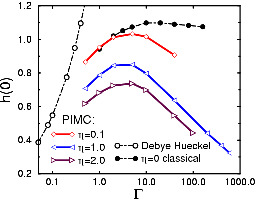Many-body enhancement of nuclear reaction rates h(0) as function of the coupling parameter.
|
Dense plasma effects can cause an exponenial change in charge particle
nuclear reaction rates important in stellar evolution.
In this article, reaction rates
in dense plasmas are examined using path integral Monte Carlo. Quantum
effects causes a reduction in the many body enhancement of the
reaction rate, h(0), compared to the classical value. This is shown in
figure on the left for different quantum parameters. This reduction
can be attributed to the "quantum smearing" of the Coulomb interaction
at the short range resulting in a reduced repulsion between the
reacting pair and surrounding particles.
|
| |
|
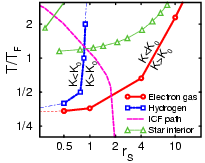Temperature density region of kinetic energy lowering for dense hydrogen and the electron gas.
|
The equilibrium momentum distribution is of fundamental importance to
characterize many-body systems. In contrast to classical systems where
the distribution is always Maxwellian, in quantum systems the
distribution depends on particle statistics, bosons or fermions, as
well as on interactions and can display interparticle correlations,
which are the basis of superfluidity and superconductivity.
In this article, we
report and explain a surprising effect of interactions in quantum
systems on the one particle momentum distribution and kinetic
energy. Interactions never lower the ground state kinetic energy of a
quantum system. However, at nonzero temperature, where the system
occupies a thermal distribution of states, interactions can reduce the
kinetic energy below the noninteracting value. This is
demonstrated using PIMC simulations for dense hydrogen and the electron gas.
|
|
|
|
 |
 |
 |
| Molecular liquid |
Molecular metallic liquid |
Metallic liquid |
|
|
|
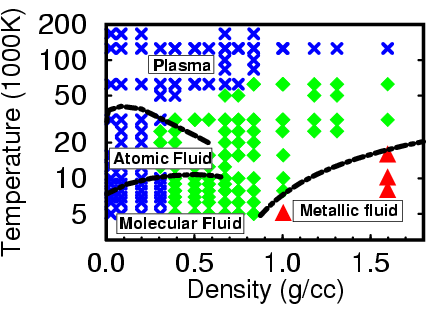At which pressure and density does hydrogen become metallic?
|
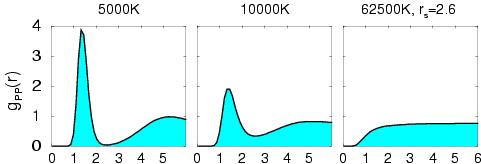At low densities up to about rs=2.6, the properties of hydrogen including
the equation of state are well understood. Processes like the thermal dissociation of molecules
can be modelled accurately with PIMC. The resulting proton-proton pair correlation functions are shown.
|
|
|
|
|
|
|
|
| 156. |
B. Militzer, "Phase Separation of Planetary Ices Explains Nondipolar Magnetic Fields of Uranus and Neptune",
Proceedings of the National Academy of Sciences 121 (2024) e2403981121. DOI: 10.1073/pnas.240398112.
|
| 155. |
K. de Villa, F. Gonzalez-Cataldo, B. Militzer, "Experimental Pathways for Detecting Double Superionicity in Planetary Ices",
submitted to Contributions to Plasmas Physics (2024). Available on the arXiv.
|
| 154. |
B. Militzer, "Ensemble Monte Carlo Calculations with Five Novel Moves",
Computer Physics Communications 309 (2025) 109424. Our C++ source code is available at DOI 10.5281/zenodo.13961174
and the manuscripts on the arXiv.
|
| 153. |
A.C. Li, B. Li, F. Gonzalez-Cataldo, R.E. Rudd, B. Militzer, E.M. Bringae, M.A. Meyers, "Diamond under extremes",
Materials Science & Engineering R 161 (2024) 100857. DOI: 10.1016/j.mser.2024.100857
|
| 152. |
X. Wang, N. Geng, K. de Villa, B. Militzer, E. Zurek, "Superconductivity in Dilute Hydrides of Ammonia under Pressure",
Physical Chemistry Letters 15 (2024) 5947. DOI: 10.1021/acs.jpclett.4c01223
|
| 151. |
M. Bonitz, J. Vorberger, M. Bethkenhagen, M. P. Bohme, D. M. Ceperley, A. Filinov, F. Graziani, G. Gregori, P. Hamann, S. B. Hansen, M. Holzmann, S. Hu, H. Kahlert, V. Karasiev, U. Kleinschmidt, L. Kordts, C. Makait, B. Militzer, Z. A. Moldabekov, C. Pierleoni, M. Preising, K. Ramakrishna, R. Redmer, S. Schwalbe, P. Svensson, T. Dornheim, "First principles simulations of dense hydrogen", Physics of Plasmas 31 (2024) 110501. DOI 10.1063/5.0219405 Available on the arXiv.
|
| 150. |
B. Militzer, W. B. Hubbard,
"Study of Jupiter's Interior: Comparison of 2, 3, 4, 5, and 6 Layer Models",
Icarus 411 (2024) 115955. DOI 10.1016/j.icarus.2024.115955. Our models for Jupiter's interior are available as a machine readable file mrt_files_05-28-23.tgz and also on 10.5281/zenodo.10471389. Available on the arXiv.
|
| 149. |
K. de Villa, F. Gonzalez-Cataldo, B. Militzer,
"Double Superionicity in Icy Compounds at Planetary Interior Conditions",
Nature Communications 14 (2023) 7580. DOI 10.1038/s41467-023-42958-0. Highlighted by Nat. Comm. editor and in this NERSC article.
|
| 148. |
H. Cao, J. Bloxham, R. S. Park, B. Militzer, R. K. Yadav, L. Kulowski, D. J. Stevenson, S. J. Bolton,
"Strong resemblance between surface and deep zonal winds inside Jupiter revealed by high-degree gravity moments",
Astrophysical Journal 959 (2023) 78. DOI: 10.3847/1538-4357/ad0cbb. Available on the arXiv.
|
| 147. |
F. Gonzalez-Cataldo, B. Militzer,
"Ab initio determination of iron melting at terapascal pressures and Super-Earths core crystallization",
Physical Review Research 5 (2023) 033194. DOI: 10.1103/PhysRevResearch.5.033194. EOS tables for the solid phase and the liquid phase.
|
| 146. |
B. Militzer,
"Study of Jupiter's Interior with Quadratic Monte Carlo Simulations",
Astrophysical J. 953 (2023) 111. DOI: 10.3847/1538-4357/ace1f1 Here we provide our open QMC source code. Available on the arXiv. Data files for different interior models and gravity harmonics:
1a,
1b,
2a,
2b,
3a and
3b.
|
| 145. |
F. Gonzalez-Cataldo, B. Militzer,
"Structural and Thermodynamic Properties of Magnesium-Rich Liquids at Ultrahigh Pressure",
Minerals 13 (2023) 885. DOI: 10.3390/min13070885.
|
| 144. |
B. Militzer, W. B. Hubbard,
"Relation of Gravity, Winds, and the Moment of Inertia of Jupiter and Saturn",
Planet. Sci. J. 4 (2023) 95. DOI: 10.3847/PSJ/acd2cd Available on the arXiv
|
| 143. |
T. Kovacevic, F. Gonzalez-Cataldo, B. Militzer,
"The homogeneous mixing of MgO and H2O at extreme conditions",
Contrib. Plasma Phys. (2023) e202300017. DOI: 10.1002/ctpp.202300017
|
| 142. |
S. Howard, T. Guillot, M. Bazot, Y. Miguel, D. J. Stevenson, E. Galanti, Y. Kaspi, W. B. Hubbard, B. Militzer, R. Helled, N. Nettelmann, B. Idini, and S. Bolton,
"Jupiter's Interior from Juno: Equations of State Uncertainties and Dilute Core Extent", Astronomy and Astrophysics 672 (2023) A33.
| | 141. |
K. M. Moore, A. Barik, S. Stanley, D. J. Stevenson, N. Nettelmann, R. Helled, T. Guillot, B. Militzer, S. Bolton,
"Dynamo Simulations of Jupiter's Magnetic Field: The Role of Stable Stratification and a Dilute Core",
JGR Planets 127 (2022) e2022JE007479.
|
| 140. |
J. Wisdom, R. Dbouk, B. Militzer, W. B. Hubbard, F. Nimmo, B. Downey, R. French,
"Loss of a satellite could explain Saturn's obliquity and young rings",
Science 377 (2022) 1285.
|
| 139. |
B. Militzer, W.B. Hubbard, S. Wahl, J.I. Lunine, E. Galanti, Y. Kaspi, Y. Miguel, T. Guillot, K. M. Moore, M. Parisi, J.E.P. Connerney, R. Helled, H. Cao, C. Mankovich, D. J. Stevenson, R. S. Park, M. Wong, S. K. Atreya, J. Anderson, S.J. Bolton,
"Juno Spacecraft Measurements of Jupiter's Gravity Imply a Dilute Core",
Planet. Sci. J. 3 (2022) 185. Data file for interior model.
|
| 138. |
T. Kovacevic, F. Gonzalez-Cataldo, S. T. Stewart, B. Militzer,
"Miscibility of rock and ice in the interiors of water worlds",
Scientific Reports 12 (2022) 13055.
|
| 137. |
R. Helled, D.J. Stevenson, J.I. Lunine, S.J. Bolton, N. Nettelmann, S. Atreya, T. Guillot, B. Militzer, Y. Miguel, W.B. Hubbard,
"Revelations on Jupiter's Formation, Evolution and Interior: Challenges from Juno Results",
Icarus 378 (2022) 114937.
|
| 136. |
Y. Miguel, M. Bazot, T. Guillot, S. Howard, E. Galanti, Y. Kaspi, W. B. Hubbard, B. Militzer, R. Helled, S. K. Atreya, J. E. P. Connerney, D. Durante, L. Kulowski, J. I. Lunine, D. Stevenson, S. Bolton,
"Jupiter's inhomogeneous envelope", Astronomy and Astrophys. 662 (2022) A18.
| | 135. |
Y.-J. Kim, B. Militzer, B. Boates, S, Bonev, P.M. Celliers, G.W. Collins, K.P. Driver, D.E. Fratanduono, S. Hamel, R. Jeanloz, J.R. Rygg, D.C. Swift, J.H. Eggert, M. Millot,
"Evidence for Dissociation and Ionization in Shock Compressed Nitrogen to 800 GPa",
Phys. Rev. Lett. 129 (2022) 015701.
|
| 134. |
J. Wu, F. Gonzalez-Cataldo, F. Soubiran, B. Militzer,
"The phase diagrams of beryllium and magnesium oxide at megabar pressures",
J. Phys. Cond. Matt. 34 (2022) 144003.
|
| 133. |
R. Akiba, A. Ermakov, B. Militzer,
"Probing the icy shell structure of ocean worlds with gravity-topography admittance",
Planetary Science J. 3 (2022) 53.
|
| 132. |
A. E. Gleason, D. R. Rittman, C. A. Bolme, E. Galtier, H. J. Lee, E. Granados, S. Ali, A. Lazicki, D. Swift, P. Celliers, B. Militzer, S. Stanley, W.L. Mao,
"Dynamically compressed water to 200 GPa: implications for ice giant interiors",
Science Advances 12 (2022) 715.
|
| 131. |
T. Dornheim, Z. A. Moldabekov, J. Vorberger, B. Militzer,
"Path Integral Monte Carlo Approach to the Structural Properties and Collective Excitations of liquid 3He without Fixed Nodes",
Scientific Reports 12 (2022) 708.
|
| 130. |
F. Gonzalez-Cataldo, B.K. Godwal, K. Driver, R. Jeanloz, B. Militzer,
"A Model of Ramp Compression of Diamond from Ab Initio Simulations",
Phys. Rev. B 104 (2021) 134104. DOI: 10.1103/PhysRevB.104.134104
|
| 129. |
S. M. Wahl, D. Thorngren, T. Lu, B. Militzer,
"Tidal Response and Shape of Hot Jupiters",
Astrophysical J. 921 (2021) 105. DOI: 10.3847/1538-4357/ac1a72 Available on the arXiv
|
| 128. |
T. Dornheim, M. Boehme, B. Militzer, J. Vorberger,
"Momentum distribution of the Uniform Electron Gas at finite temperature: Effects of spin-polarization",
Phys. Rev. E 104 (2021) 055205. DOI: 10.1103/PhysRevE.104.055206. Available on the arXiv.
|
| 127. |
J. Wu, F. Gonzalez-Cataldo, B. Militzer,
"High Pressure Phase Diagram of Beryllium from Ab Initio Free Energy Calculations",
Phys. Rev. B 104 (2021) 014103. DOI: 10.1103/PhysRevB.104.014103. Available on the arXiv.
|
| 126. |
T. Dornheim, M. Boehme, B. Militzer, J. Vorberger,
"Ab initio path integral Monte Carlo approach to the momentum distribution of the uniform electron gas at finite temperature without fixed nodes",
Phys. Rev. B 103 (2021) 205142. DOI: 10.1103/PhysRevB.103.205142. Available on the arXiv.
|
| 125. |
G. Massacrier, M. Boehme, J. Vorberger, F. Soubiran, B. Militzer,
"Reconciling Ionization Energies and Band Gaps of Warm Dense Matter Derived with Ab Initio Simulations and Average Atom Models",
Phys. Rev. Res. 3 (2021) 023026. DOI: 10.1103/PhysRevResearch.3.023026.
|
| 124. |
H. D. Whitley, G. E. Kemp, C. Yeamans, Z. Walters, B. E. Blue, W.Garbett, M. Schneider, R. S. Craxton, E. M. Garcia, P. W. McKenty, M. Gatu-Johnson, K. Caspersen, J. I. Castor, M. Dane, C. L. Ellison, J. Gaffney, F. R. Graziani, J. Klepeis, N. Kostinski, A. Kritcher, B. Lahmann, A. E. Lazicki, H. P. Le, R. A. London, B. Maddox, M. Marshall, M. E. Martin, B. Militzer, A. Nikroo, J. Nilsen, T. Ogitsu, J. Pask, J. E. Pino, M. Rubery, R. Shepherd, P. A. Sterne, D. C. Swift, L. Yang, S. Zhang
"Comparison of ablators for the polar direct drive exploding pusher platform",
J. High Energy Density Physics 38 (2021) 100928. DOI: 10.1016/j.hedp.2021.100928 Available on the arXiv.
|
| 123. |
B. Militzer, F. Gonzalez-Cataldo, S. Zhang, K. P. Driver, F. Soubiran,
"First-principles equation of state database for warm dense matter computation",
Phys. Rev. E 103 (2021) 013203. DOI: 10.1103/PhysRevE.103.013203 Available on the arXiv. Click here to reach our FPEOS webpage.
|
| 122. |
R. Domingos, M. M. Tremblay, D. L. Shuster, B. Militzer,
"Simulations and experiments reveal effect of nanopores on helium diffusion in quartz",
ACS Earth and Space Chemistry 4 (2020) 1906. DOI: 10.1021/acsearthspacechem.0c00187
|
| 121. |
B. Militzer, F. Gonzalez-Cataldo, S. Zhang, H. D. Whitley, D. C. Swift, M. Millot,
"Nonideal Mixing Effects in Warm Dense Matter Studied with First-Principles Computer Simulations",
J. Chem. Phys. 153 (2020) 184101. DOI: 10.1063/5.0023232. Available on the arXiv.
|
| 120. |
F. Soubiran, B. Militzer,
"Anharmonicity and Phase Diagram of Magnesium Oxide in the Megabar Regime",
Phys. Rev. Lett. 125 (2020) 175701. DOI: 10.1103/PhysRevLett.125.175701.
|
| 119. |
F. Gonzalez-Cataldo, F. Soubiran, B. Militzer,
"Equation of State of Hot, Dense Magnesium Derived with First-Principles Computer Simulations",
Physics of Plasmas 27 (2020) 092706. DOI: 10.1063/5.0017555. Available on the arXiv.
| | 118. |
M. A. Olson, S. Bhatia, P. Larson, B. Militzer,
"Prediction of Chlorine and Fluorine Crystal Structures at High Pressure Using Symmetry Driven Structure Search with Geometric Constraints",
J. Phys. Chem. 153 (2020) 094111. Available on the arXiv.
| | 117. |
S. Zhang, M. C. Marshall, L. H. Yang, P. A. Sterne, B. Militzer, M. Daene, J. A. Gaffney, A. Shamp, T. Ogitsu, K. Caspersen, A. E. Lazicki, D. Erskine, R. A. London, P. M. Celliers, J. Nilsen, H. D. Whitley,
"Benchmarking boron carbide equation of state using computation and experiment",
Phys. Rev. E 102 (2020) 053203. Available on the arXiv.
| | 116. |
F. Gonzalez-Cataldo, B. Militzer,
"Thermal and Pressure Ionization in Warm, Dense MgSiO3 Studied with First-Principles Computer Simulations",
AIP Conference Proceedings 2272 (2020) 090001. DOI: 10.1063/12.0000793. Available on the arXiv.
| | 115. |
S. M. Wahl, M. Parisi, W. M . Folkner, W. B. Hubbard, B. Militzer,
"Equilibrium Tidal Response of Jupiter: Detectability by Juno Spacecraft",
Astrophys. J. 891:42 (2020) 1 (DOI).
| | 114. |
M. Millot, S. Zhang, D. E. Fratanduono, F. Coppari, S. Hamel, B. Militzer, D. Simonova, S. Shcheka, N. Dubrovinskaia, L. Dubrovinsky, J. H. Eggert,
"Recreating giants impacts in the laboratory: Shock compression of MgSiO3 bridgmanite to 14 Mbar",
Geophys. Res. Lett. 47 (2020) e2019GL085476.
| | 113. |
F. Gonzalez-Cataldo, F. Soubiran, H. Peterson, B. Militzer,
"Path Integral Monte Carlo and Density Functional Molecular Dynamics Simulations of Warm, Dense MgSiO3",
Phys. Rev. B 101 (2020) 024107. Available on the arXiv.
| | 112. |
F. Soubiran, F. Gonzalez-Cataldo, K. P. Driver, S. Zhang, B. Militzer,
"Magnesium Oxide at Extreme Temperatures and Pressures Studied with First-Principles Simulations",
J. Chem. Phys. 151 (2019) 214104.
| | 111. |
B. Militzer, S. Wahl, W. B. Hubbard,
"Models of Saturn's Interior Constructed with an Accelerated Concentric Maclaurin Spheroid Method",
Astrophysical Journal 879 (2019) 78. Available on the arXiv.
| | 110. |
S. Zhang, A. Lazicki, B. Militzer, L. H. Yang, K. Caspersen, J. A. Gaffney, M. W. Däne, J. E. Pask, W. R. Johnson, A. Sharma, P. Suryanarayana, D. D. Johnson, A. V. Smirnov, P. A. Sterne, D. Erskine, R. A. London, F. Coppari, D. Swift, J. Nilsen, A. J. Nelson, H. D. Whitley, "Equation of state of warm-dense boron nitride combining computation, modeling, and experiment", Phys. Rev. B 99 (2019) 165103. Available on the arXiv.
| | 109. |
L. Iess, B. Militzer, Y. Kaspi, P. Nicholson, D. Durante, P. Racioppa, A. Anabtawi, E. Galanti, W. Hubbard, M. J. Mariani, P. Tortora, S. Wahl, M. Zannoni,
"Measurement and implications of Saturn's gravity field and ring mass", Science 17 Jan 2019:eaat2965. DOI: 10.1126/science.aat2965.
| | 108. |
B. Militzer, E. L. Pollock, D. Ceperley,
"Path Integral Monte Carlo Calculation of the Momentum Distribution of the Homogeneous Electron Gas at Finite Temperature", J. High Energy Density Physics 30 (2019) 13-20.
| | 107. |
R. Domingos, K. M. Shaik, B. Militzer,
"Prediction of Novel High Pressure H2O-NaCl and Carbon Oxide Compounds with Symmetry-Driven Structure Search Algorithm", Phys. Rev. B 98 (2018) 174107. Also available on the arXiv. |
| 106. |
F. Soubiran, B. Miltzer,
"Electrical conductivity and magnetic dynamos in magma oceans of Super-Earths",
Nature Communications 9 (2018) 3883. |
| 105. |
S. Zhang, B. Militzer, M. C. Gregor, K. Caspersen, L. H. Yang, T. Ogitsu, D. Swift, A. Lazicki, D. Erskine, R. A. London, P. M. Celliers, J. Nilsen, P. A. Sterne, and H. D. Whitley
"Theoretical and experimental investigation of the equation of state of boron plasmas",
Phys. Rev. E 98 (2018) 023205, available on the arXiv. |
| 104. |
K. P. Driver, F. Soubiran, B. Militzer,
"Path integral Monte Carlo simulations of hot, dense aluminum",
Physical Review E 97 (2018) 063207.
|
| 103. |
L. Iess, W. M. Folkner, D. Durante, M. Parisi, Y. Kaspi, E. Galanti,
T. Guillot, W. B. Hubbard, D. J. Stevenson, J. D. Anderson,
D. R. Buccino, L. Gomez Casajus, A. Milani, R. Park, P. Racioppa,
D. Serra, P. Tortora, M. Zannoni, H. Cao, R. Helled, J. I. Lunine,
Y. Miguel, B. Militzer, S. Wahl, J. E. P. Connerney, S. M. Levin,
S. J. Bolton,
"Measurement
of Jupiter's asymmetric gravity field",
Nature 555 (2018) 220. |
| 102. |
Y. Kaspi, E. Galanti, W. B. Hubbard, D. J. Stevenson, S. J. Bolton,
L. Iess, T. Guillot, J. Bloxham, J. E. P. Connerney, H. Cao,
D. Durante, W. M. Folkner, R. Helled, A. P. Ingersoll, S. M. Levin,
J. I. Lunine, Y. Miguel, B. Militzer, M. Parisi, S. M. Wahl
"Jupiter's
atmospheric jet streams extend thousands of kilometres deep",
Nature 555 (2018) 223. |
| 101. |
T. Guillot, Y. Miguel, B. Militzer, W. B. Hubbard, Y. Kaspi,
E. Galanti, H. Cao, R. Helled, S. M. Wahl, L. Iess, W. M. Folkner,
D. J. Stevenson, J. I. Lunine, D. R.
Reese, A. Biekman, M. Parisi,
D. Durante, J. E. P. Connerney, S. M. Levin & S. J. Bolton,
"A suppression
of differential rotation in Jupiter's deep interior", Nature 555 (2018) 227. |
| 100. |
B. Militzer, S. Zhang,
"Ab initio Simulations of Superionic H2O, H2O2, and H9O4 Compounds",
AIP conference proceedings 1979 (2018) 050012. Also available on the arXiv. |
| 99. |
S. Zhang, B. Militzer, L. X. Benedict, F. Soubiran, K. P. Driver, P. A. Sterne,
"Path integral Monte Carlo simulations of dense carbon-hydrogen plasmas",
J. Chem. Phys. 148 (2018) 102318. Also available on the arXiv. |
| 98. |
Y. Kaspi, T. Guillot, E. Galanti, Y. Miguel, R. Helled, W. B. Hubbard, B. Militzer, S. M. Wahl, S. Levin, J. E. P. Connerney, S. J. Bolton,
"The effect of differential rotation on Jupiter's low-degree even gravity moments",
Geophysical Research Letters 44 (2017) 5960, doi:10.1002/2017GL073629.
|
| 97. |
S. Zhang, K. P. Driver, F. Soubiran, B. Militzer
"First-principles Equation of State and Shock Compression Predictions of Warm Dense Hydrocarbons",
Phys. Rev. E 96 (2017) 013204. |
| 96. |
K. P. Driver, B. Militzer,
"First-principles simulations of warm dense lithium fluoride",
Phys. Rev. E 95 (2017) 043205.
Also availalbe on the arXiv. |
| 95. |
S. M. Wahl, W. B. Hubbard, B. Militzer, T. Guillot, Y. Miguel, Y. Kaspi, R. Helled, D. Reese, N. Movshovitz, E. Galanti, S. Levin, J.E. Connerney, S.J. Bolton,
"Comparing Jupiter interior structure models to Juno gravity measurements and the role of a dilute core",
Geophysical Research Letters 44 (2017) 4649, doi:10.1002/2017GL073160.
|
| 94. |
K. P. Driver, F. Soubiran, S. Zhang, B. Militzer,
"Comparison of Path Integral Monte Carlo Simulations of Helium, Carbon, Nitrogen, Oxygen, Water, Neon, and Silicon Plasmas",
J. High Energy Density Physics 23 (2017) 81.
|
| 93. |
F. Soubiran, B. Militzer, K. P. Driver, S. Zhang,
"Properties of hydrogen, helium, and silicon dioxide mixtures in giant planet interiors",
Physics of Plasmas 24 (2017) 041401. Also available on the arXiv.
|
| 92. |
S. Zhang, K. P. Driver, F. Soubiran, B. Militzer,
"Equation of state and shock compression of warm dense sodium - A first-principle study",
J. Chem. Phys. 146 (2017) 074505. Also available on the arXiv.
|
| 91. |
T. Leonhardi, B. Militzer,
"Ab initio simulations of liquid carbon monoxide at high pressure",
J. High Energy Density Physics 22 (2017) 41.
|
| 90. |
Z. Li, J. Li, L. Rebecca, J. Liu, B. Militzer,
"Determination of calcium carbonate and sodium carbonate melting curves up to Earth's transition zone pressures with implications for the deep carbon cycle",
Earth and Planetary Science Letters 457 (2017) 395.
|
| 89. |
S. Zhang, K. P. Driver, F. Soubiran, B. Militzer,
"Path Integral Monte Carlo Simulations of Warm Dense Sodium",
J. High Energy Density Physics 21 (2016) 16.
|
| 88. |
B. Militzer,
"Supercell Design for First-Principles Simulations of Solids and Application to Diamond, Silica, and Superionic Water",
J. High Energy Density Physics 21 (2016) 8.
|
| 87. |
S. X. Hu, B. Militzer, L. A. Collins, K. P. Driver, and J. D. Kress,
"First-Principles Prediction of the Softening of the Silicon Shock Hugoniot Curve",
Phys. Rev. B 94 (2016) 094109. Also available on the arXiv. |
| 86. |
B. Militzer, F. Soubiran, S. M. Wahl, W. Hubbard,
"Understanding Jupiter's Interior",
J. Geophysical Research, 121 (2016) 1552. Also available on the arXiv. |
| 85. |
S. M. Wahl, W. B. Hubbard, B. Militzer,
"Tidal response of preliminary Jupiter model",
Astrophysical J. 831 (2016) 14. Also available on the arXiv. |
| 84. |
F. Soubiran, B. Militzer,
"The properties of heavy elements in giant planet envelopes",
Astrophysical J. 829 (2016) 14. Also available on the arXiv.
| | 83. |
B. Militzer,
"Computation of the High Temperature Coulomb Density Matrix in Periodic Boundary Conditions", Computer Physics Communications 204 (2016) 88. Also available on the
arXiv.
| | 82. |
S. M. Wahl, W. B. Hubbard, B. Militzer,
"The Concentric Maclaurin Spheroid method with tides and a rotational enhancement of Saturn's tidal response",
Icarus 282 (2017) 183. Also available on the arXiv. |
| 81. |
W. B. Hubbard, B. Militzer,
"A preliminary Jupiter model",
Astrophysical Journal 820 (2016) 80.
Also available on the arXiv. |
| 80. |
K. P. Driver, B. Militzer,
"First-Principles Equation of State Calculations of Warm Dense Nitrogen",
Phys. Rev. B 93 (2016) 064101. |
| 79. |
S. Zhang, S. Cottaar, T. Liu, S. Stackhouse, B. Militzer,
"High-pressure, temperature elasticity of Fe- and Al-bearing MgSiO3: implications for the Earth's lower mantle",
Earth and Planetary Science Letters 434 (2016) 264. |
| 78. |
B. Militzer, K. P Driver,
"Development of Path Integral Monte Carlo Simulations with Localized Nodal Surfaces for Second-Row Elements",
Phys. Rev. Lett. 115 (2015) 176403. |
| 77. |
K. P. Driver, F. Soubiran, Shuai Zhang, and B. Militzer
"First-principles equation of state and electronic properties of warm dense oxygen",
J. Chem. Phys. 143 (2015) 164507. |
| 76. |
F. Soubiran, B. Militzer,
"Miscibility calculations for water and hydrogen in giant planets",
Astrophys. J. 806 (2015) 228. |
| 75. |
S. X. Hu, V. N. Goncharov, T. R. Boehly, R. L. McCrory, S. Skupsky, L. A. Collins, J. D. Kress, B. Militzer,
"Impact of First-Principles Properties of Deuterium-Tritium on Inertial Confinement Fusion Target Designs",
Physics of Plasmas 22 (2015) 056304. |
| 74. |
F. Soubiran, B. Militzer,
"Hydrogen-Water Mixtures in Giant Planet Interiors Studied with Ab Initio Simulations",
J. High Energy Density Physics 17 (2015) 157. |
| 73. |
K. Driver, B. Militzer,
"First-principles simulations and shock Hugoniot calculations of warm dense neon",
Phys. Rev. B 91 (2015) 045103. |
| 72. |
S. Wahl, B. Militzer,
"High-temperature miscibility of iron and rock during terrestrial planet formation",
Earth and Planetary Science Letters 410 (2015) 25. |
| 71. |
Y. Lin, R. E. Cohen, S. Stackhouse, K. P. Driver, B. Militzer, L. Shulenburger and J. Kim,
"Equations of state and stability of MgSiO3 perovskite and post-perovskite phases from quantum Monte Carlo simulations",
Phys. Rev. B 90 (2014) 184103, available on the archive. |
| 70. |
H. F. Wilson, B. Militzer,
"Interior phase transformations and mass-radius relationships of silicon-carbon planets",
Astrophys. J. 973 (2014) 34. |
| 69. |
F. Gonzalez-Cataldo, H. F. Wilson, B. Militzer,
"Solubility of silica in metallic hydrogen: implications for the stability of rocky cores in giant planets",
Astrophys. J. 787 (2014) 79. |
| 68. |
P. Kaercher, B. Militzer, H.-R. Wenk,
"Ab initio calculatios of elastic constants in plagioclase feldspars",
American Mineralogist 99 (2014) 2344. |
| 67. |
L. X. Benedict, K. P. Driver, S. Hamel, B. Militzer, T. Qi, A. A. Correa, A. Saul, E. Schwegler,
"A multiphase equation of state for carbon addressing high pressures and temperatures",
Phys. Rev. B 89 (2014) 224109, available on cond-mat. |
| 66. |
S. M. Wahl, H. F. Wilson, B. Militzer,
"Solubility of iron in metallic hydrogen and stability of dense cores in giant planets",
Astrophysical Journal 773 (2013) 95, available on astro-ph. |
| 65. |
B. Militzer, W. B. Hubbard,
"Ab Initio Equation of State for Hydrogen-Helium Mixtures with Recalibration of the Giant-Planet Mass-Radius Relation",
Astrophysical Journal 774 (2013) 148, available on astro-ph. |
| 64. |
B. K. Godwal, S. Stackhouse, J. Yan, S. Speziale, B. Militzer, R. Jeanloz,
"Co-Determination
of Crystal Structures at High Pressure: Combined Application of Theory
and Experiment to the Intermetallic Compound AuGa2",
Phys. Rev. B Rapid Comm. 87 (2013) 100101. |
| 63. |
B. Militzer,
"Equation of state calculations of hydrogen-helium mixtures in solar and extrasolar giant planets",
Physical Review B 87 (2013) 014202. |
| 62. |
H. F. Wilson, M. L. Wong, B. Militzer,
"Superionic to superionic phase change in water: consequences for the interiors of Uranus and Neptune",
Physical Review Letters 110 (2013) 151102, also available on astro-ph. |
| 61. |
S. Zhang, H. F. Wilson, K. P. Driver, B. Militzer,
"H4O and other hydrogen-oxygen compounds at giant-planet core pressures",
Physical Review B 87 (2013) 024112, also available on condmat. |
| 60. |
B. L. Sherman, H. F. Wilson, D. Weeraratne, and B. Militzer,
"Ab Initio Simulations of Hot, Dense Methane During Shock Experiments",
Physical Review B 86 (2012) 224113,
also available on condmat. |
| 59. |
B. Militzer,
"Ab Initio Investigation of a Possible Liquid-Liquid Phase Transition in MgSiO3 at Megabar Pressures",
Journal of High Energy Density Physics 9 (2013) 152, available also on condmat. |
| 58. |
K. P. Driver, B. Militzer,
"All-Electron Path Integral Monte Carlo Simulations of Warm Dense Matter: Application to Water and Carbon Plasmas",
Phys. Rev. Lett. 108 (2012) 115502.
| | 57. |
H. F. Wilson, B. Militzer,
"Rocky core solubility in Jupiter and giant exoplanets",
Phys. Rev. Lett. 108 (2012) 111101. Suggested read by PRL editor. Also available on astro-ph. |
| 56. |
S. X. Hu, B. Militzer, V. N. Goncharov, and S. Skupsky,
"FPEOS: A First-Principles Equation of State Table of Deuterium for Inertial Confinement Fusion Applications",
Phys. Rev. B, 84 (2011) 224109, also available on cond-mat. |
| 55. |
H. F. Wilson, B. Militzer,
"Solubility of water ice in metallic hydrogen: consequences for core erosion in gas giant planets",
Astrophys. J. 745 (2012) 54, also available on astro-ph.
| | 54. |
B. Militzer,
"Bonding and Electronic Properties of Ice at High Pressure",
Intern. J. Quantum Chemistry 112 (2011) 314,
also available on cond-mat.
| | 53. |
L. Miyagi, W. Kanitpanyacharoen, S. Stackhouse, B. Militzer, H.-R. Wenk,
"The Enigma of Post-Perovskite Anisotropy: Deformation versus Transformation Textures",
Physics and Chemistry of Minerals 38 (2011) 665, DOI: 10.1007/10.1007/s00269-011-0439-y.
| | 52. |
B. Militzer, H. F. Wilson,
"New Phases of Water Ice Predicted at Megabar Pressures",
Phys. Rev. Lett. 105 (2010) 195701, available on cond-mat.
| | 51. |
S. X. Hu, B. Militzer, V. N. Goncharov, and S. Skupsky,
"Strong-Coupling and Degeneracy Effects in Inertial Confinement Fusion Implosions",
Phys. Rev. Lett. 104 (2010) 235003.
| | 50. |
B. Militzer, H.-R. Wenk, S. Stackhouse, and L. Stixrude,
"First-Principles Calculation of the Elastic Moduli of Sheet Silicates and their Application to Shale Anisotropy", American Mineralogist 96 (2011) 125.
| | 49. |
A. R. Rhoden, B. Militzer, E. M. Huff, T. A. Hurford, M. Manga, and M. A. Richards,
"Constraints on Europa's rotational dynamics from modeling of tidally-driven fractures",
Icarus 210 (2010) 770.
| | 48. |
H. F. Wilson and B. Militzer,
"Sequestration of noble gases in giant planet interiors", Phys. Rev. Lett. 104 (2010) 121101. Read commentary by J. Fortney "Peering into Jupiter" in Physics 3 (2010) 26, UC Berkeley's press release, Discovery Channel and LA Times articles.
| | 47. |
K. P. Esler, R. E. Cohen, B. Militzer, J. Kim, R.J. Needs, and M.D. Towler,
"Fundamental high pressure calibration from all-electron quantum Monte Carlo calculations", Phys. Rev. Lett. 104 (2010) 185702.
| | 46. |
K. P. Driver, R. E. Cohen, Z. Wu, B. Militzer, P. Lopez Rios, M. D. Towler, R. J. Needs, and J. W. Wilkins
"Quantum Monte Carlo for minerals at high pressures: Phase stability, equations of state, and elasticity of silica", Proc. Nat. Acad. Sci. 107 (2010) 9519. |
| 45. |
P. Beck, A.F. Goncharov, J. A. Montoya, V.V. Struzhkin, B. Militzer, R.J.
Hemley, and H.-K. Mao, ''Response to “Comment on ‘Measurement of
thermal diffusivity at high-pressure using a transient heating
technique’”'', Appl. Phys. Lett. 95 (2009) 096101. |
| 44. |
J. J. Fortney, I. Baraffe, B. Militzer, chapter "Interior Structure
and Thermal Evolution of Giant Planets", in "Exoplanets",
ed. S. Seager, Arizona Space Science series (2009).
| | 43. |
B. Militzer,
"Correlations in Hot Dense Helium", J Phys. A 42 (2009) 214001, cond-mat/09024281.
| | 42. |
J. J. Fortney, S. H. Glenzer, M. Koenig, B. Militzer, D. Saumon, and D. Valencia,
"Frontiers of the Physics of Dense Plasmas and Planetary Interiors: Experiment, Theory, Applications", Physics of Plasmas 16 (2008) 041003.
| | 41. |
B. Militzer and W. B. Hubbard,
"Comparison of Jupiter Interior Models Derived from First-Principles Simulations", Astrophysics and Space Science 322 (2009) 129, astro-ph/08074266.
| | 40. |
S. A. Khairallah and B. Militzer,
"First-Principles Studies of the Metallization and the Equation of State of Solid Helium", Phys. Rev. Lett. 101 (2008) 106407, physics/08054433.
| | 39. |
B. Militzer,
"Path Integral Monte Carlo and Density Functional Molecular Dynamics Simulations of Hot, Dense Helium", Phys. Rev. B 79 (2009) 155105, cond-mat/08050317.
| | 38. |
B. Militzer, W. B. Hubbard, J. Vorberger, I. Tamblyn, and S.A. Bonev,
"A Massive Core in Jupiter Predicted From First-Principles Simulations",
Astrophysical Journal Letters 688 (2008) L45, astro-ph/08074264.
| | 37. |
P. Beck, A. F. Goncharov, V. Struzhkin, B. Militzer, H.-K. Mao, and R. J. Hemley
"Measurement of thermal diffusivity at high pressure using a transient heating technique",
Appl. Phys. Lett. 91 (2007) 181914.
| | 36. |
B. Militzer, W. B. Hubbard,
"Implications of Shock Wave Experiments with Precompressed Materials for Giant Planet Interiors",
AIP conference proceedings 955 (2007) 1395.
| | 35. |
J. Vorberger, I. Tamblyn, S.A. Bonev, B. Militzer,
"Properties of Dense Fluid Hydrogen and Helium in Giant Gas Planets", Contrib. Plasma Phys. 47 (2007) 375.
| | 34. |
S. Seager, M. Kuchner, C. A. Hier-Majumder, B. Militzer,
"Mass-radius relationship of solid exoplanets", Astrophys. J. 669 (2007) 1279.
| | 33. |
V. V. Struzhkin, B. Militzer, W. Mao, R. J. Hemley, H.-k. Mao,
"Hydrogen Storage in Clathrates",
Chem. Rev. 107 (2007) 4133.
| | 32. |
G. D. Cody, H. Yabuta, T. Araki, L. D. Kilcoyne, C. M. Alexander, H. Ade, P. Dera, M. Fogel, B. Militzer, B. O. Mysen,
"An Organic thermometer for Chondritic Parent Bodies",
Earth. Planet. Sci. Lett. 272 (2008) 446.
| | 31. |
J. Vorberger, I. Tamblyn, B. Militzer, S.A. Bonev,
"Hydrogen-Helium Mixtures in the Interiors of Giant Planets",
Phys. Rev. B 75 (2007) 024206, cond-mat/0609476.
| | 30. |
B. Militzer, R. J Hemley,
"Solid oxygen takes shape", Nature (News & Views), 443 (2006) 150.
| | 29. |
B. Militzer,
"First Principles Calculations of Shock Compressed Fluid Helium",
Phys. Rev. Lett. 97 (2006) 175501.
| | 28. |
B. Militzer, R. L. Graham,
"Simulations of Dense Atomic Hydrogen in the Wigner Crystal Phase", J. Phys. Chem. Solids, 67 (2006) 2136.
| | 27. |
B. Militzer,
"Hydrogen-Helium Mixtures at High Pressure", J. Low Temp. Phys. 139 (2005) 739.
| | 26. |
B. Militzer, E. L. Pollock,
"Equilibrium Contact Probabilities in Dense Plasmas", Phys. Rev. B, 71 (2005) 134303.
| | 25. |
J.-F. Lin, B. Militzer, V. V. Struzhkin, E. Gregoryanz, R. J. Hemley, H.-k. Mao,
"High Pressure-Temperature Raman Measurements of H2O Melting to 22 GPa and 900 K", J. Chem. Phys. 121 (2004) 8423.
| | 24. |
E. L. Pollock, B. Militzer,
"Dense Plasma Effects on Nuclear Reaction Rates",
Phys. Rev. Lett. 92 (2004) 021101. |
| 23. |
S. A. Bonev, B. Militzer, G. Galli,
"Dense liquid deuterium: Ab initio simulation of states obtained in gas gun shock wave experiments",
Phys. Rev. B 69 (2004) 014101. |
| 22. |
F. Brglez, X.Y. Li, M.F. Stallmann, and B. Militzer,
"Evolutionary and Alternative Algorithms: Reliable
Cost Predictions for Finding Optimal Solutions to the LABS Problem",
Information Sciences, in press, 2004.
| | 21. |
B. Militzer, F. Gygi, G. Galli,
"Structure
and Bonding of Dense Liquid Oxygen from First Principles Simulations",
Phys. Rev. Lett. 91 (2003) 265503. |
| 20. |
F. Brglez, X.Y. Li, M.F. Stallmann, and B. Militzer,
"Reliable
Cost Predictions for Finding Optimal Solutions to LABS Problem:
Evolutionary and Alternative Algorithms",
Proceedings of The Fifth International Workshop on Frontiers
in Evolutionary Algorithms, Cary, NC (2003). |
| 19. |
B. Militzer,
"Path
Integral Calculation of Shock Hugoniot Curves of Precompressed Liquid Deuterium",
J. Phys. A: Math. Gen. 63 (2003) 6159. |
| 18. |
B. Militzer, E. L. Pollock,
"Lowering
of the Kinetic Energy in Interacting Quantum Systems",
Phys. Rev. Lett. 89 (2002) 280401. |
| 17. |
B. Militzer, D. M. Ceperley, J. D. Kress, J. D. Johnson, L. A. Collins, S. Mazevet,
"Calculation
of a Deuterium Double Shock Hugoniot from Ab Initio Simulations",
Phys. Rev. Lett. 87 (2001) 275502. |
| 16. |
B. Militzer, D. M. Ceperley,
"Path Integral Monte Carlo Simulation
of the Low-Density Hydrogen Plasma",
Phys. Rev. E 63 (2001) 066404. |
| 15. |
B. Militzer, D. M. Ceperley,
"Path Integral
Monte Carlo Calculation of the Deuterium Hugoniot",
Phys. Rev. Lett. 85 (2000) 1890. |
| 14. |
B. Militzer,
"Path Integral Monte Carlo
Simulations of Hot Dense Hydrogen",
Ph.D. thesis, University of Illinois at Urbana-Champaign (2000). |
| 13. |
B. Militzer, E. L. Pollock,
"Variational Density Matrix
Method for Warm Condensed Matter and Application to Dense Hydrogen",
Phys. Rev. E 61 (2000) 3470. |
| 12. |
B. Militzer, E. L. Pollock,
"Introduction to the
Variational Density Matrix Method and its Application to Dense Hydrogen",
in Strongly Coupled Coulomb Systems 99,
ed. by C. Deutsch, B. Jancovici, and M.-M. Gombert,
J. Phys. France IV 10 (2000) 315. |
| 11. |
B. Militzer, W. Magro, and D. Ceperley,
"Characterization of the
State of Hydrogen at High Temperature and Density",
Contr. Plasma Physics 39 (1999) 1-2, 151. |
| 10. |
W. Magro, B. Militzer, D. Ceperley, B. Bernu, and C. Pierleoni,
"Restricted Path Integral Monte Carlo
Calculations of Hot, Dense Hydrogen",
in Strongly Coupled Coulomb Systems,
ed. by G. J. Kalman, J. M. Rommel and K. Blagoev, Plenum Press, New York NY, 1998. |
| 9. |
W. Ebeling, B. Militzer, and F. Schautz,
"Quasi-Classical Theory and Simulation
of Two-Component Plasmas",
in Strongly Coupled Coulomb Systems,
ed. by G. J. Kalman, J. M. Rommel and K. Blagoev, Plenum Press, New York NY, 1998. |
| 8. |
B. Militzer, W. Magro, and D. Ceperley,
"Fermionic Path-Integral Simulation
of Dense Hydrogen",
in Strongly Coupled Coulomb Systems,
ed. by G. J. Kalman, J. M. Rommel and K. Blagoev, Plenum Press, New York NY, 1998. |
| 7. |
B. Militzer, M. Zamparelli, and D. Beule,
"Evolutionary Search for
Low Autocorrelated Binary Sequences",
IEEE Trans. Evol. Comput. 2 (1998) 34-39. |
| 6. |
W. Ebeling, B. Militzer, and F. Schautz,
"Quasi-classical Theory and
Simulations of Hydrogen-like Quantum Plasmas",
Contr. Plasma Physics 37 (1997) 2-3, 137. |
| 5. |
W. Ebeling and B. Militzer,
"Quantum Molecular Dynamics
of Partially Ionized Plasmas",
Phys. Lett. A 226 (1997) 298 |
| 4. |
B. Militzer,
"Quanten-Molekular-Dynamik mit reaktiven Freiheitsgraden",
in Dynamik, Evolution, Strukturen,
ed. J. Freund, Dr. Köster
publishing company, Berlin, 1996. |
| 3. |
B. Militzer,
"Quanten-Molekular-Dynamik
von Coulomb-Systemen",
Logos publishing company, Berlin, 1996, ISBN 3-931216-08-X |
| 2. |
B.-D. Dörfel and B. Militzer,
"Test of Modular Invariance for Finite XXZ Chains",
J. Phys. A: Math. Gen. 26 (1993) 4875. |
| 1. |
A. Richter, G. Kessler, and B. Militzer,
"Growth-kinectics of thin-films deposited by laser ablation", 473-478, in
Laser Treatment of Materials, ed. by Barry L. Mordike, Oberursel : DGM Informationsgesellschaft, 1992. |
|
| |
