By Burkhard Militzer
Here we introduce a new general-purpose Quadratic Monte Carlo (QMC) technique that is more efficient in confining fitness landscapes than affine invariant method that relies on linear stretch moves. We compare how long it takes the ensembles of walkers in both methods to travel to the most relevant parameter region. Once there, we compare the autocorrelation time and error bars of the two methods. For a ring potential and the 2d Rosenbrock function, we find that our quadratic Monte Carlo technique is significantly more efficient. Furthermore we modified the walk moves by adding a scaling factor.
Here we provide the C++ source code and examples so that this method can be applied elsewhere.
Recommended citation: B. Militzer, Study of Jupiter's Interior with Quadratic Monte Carlo Simulations", Astrophysical Journal 953 (2023) 111.
 |
 |
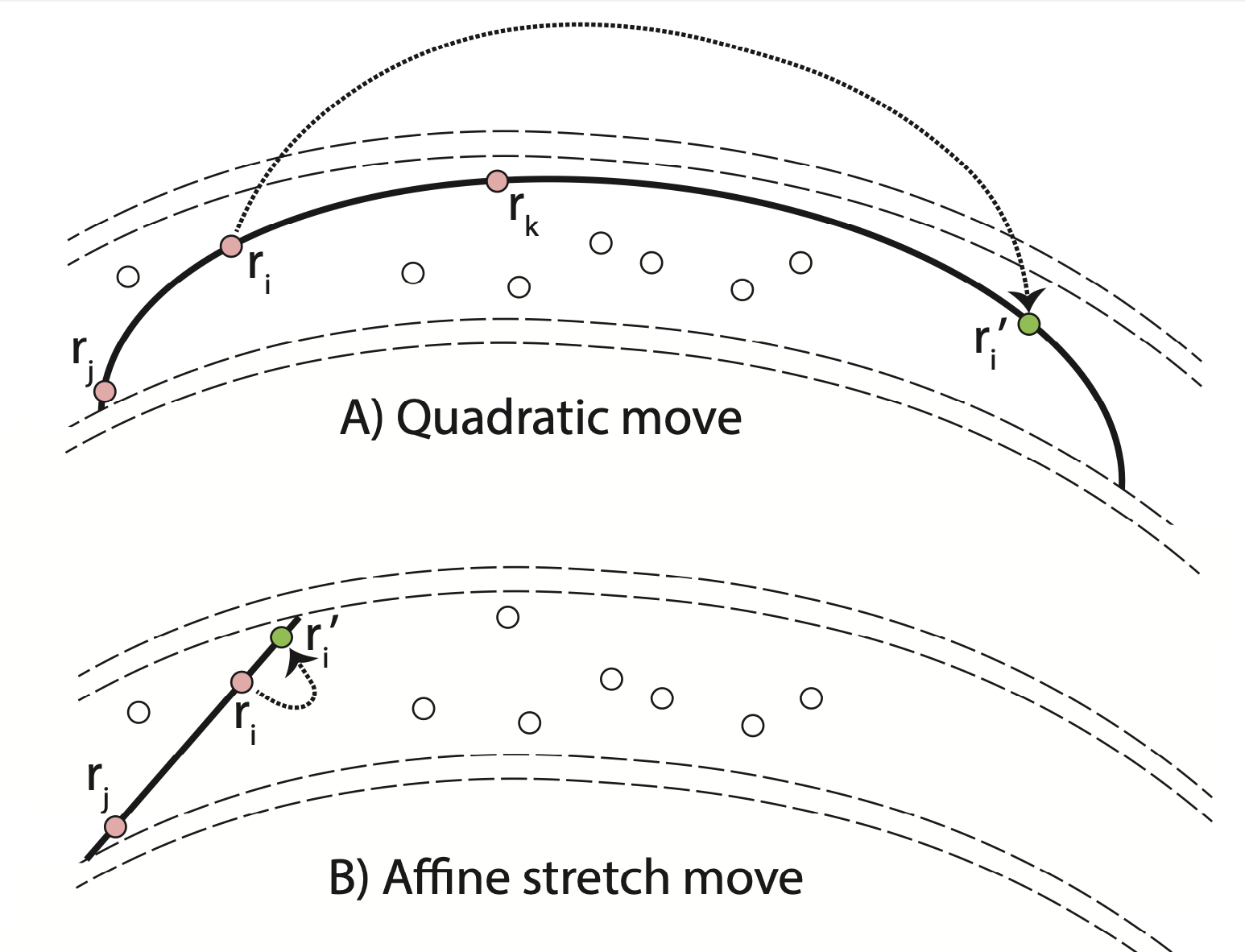
| Illustration of quadratic (top) and affine invariant (bottom) moves in a confining channel (dashed lines). For the quadratic move, two helper points rj and rk are employed to move walker i. Conversely, for the affine move, only one additional point rj is used and walker i may thus not travel as far in a single step in a curved channel. | Autocorrelation function (panel a) and error bar from blocking analysis (panel b) of affine and quadratic MC calculations. In panel (c), we compare the Monte Carlo error bar and the time it take the ensemble to travel around the ring. Compared the affine method (blue), our QMC method (red and green points) requires a travel time approximately half as long and leads to error bars half as large. |
(1) Download the latest version. Our code also has a DOI: 10.5281/zenodo.8038144
| Date |
File description | Download link |
| 08-10-23 | We report five novel ensemble Monte Carlo moves in a new manuscript that was just accepted for publication in Comp. Phys. Comm. Our updated source code was uploaded to Zenodo and is available here: | qmc_08-10-23.tar.gz |
| 03-08-23 | Code submitted along with accepted version of our manuscript. We added code to sample the 2d Rosenbrock function. | qmc_03-08-23.tar.gz |
| 07-03-22 | Submitted along with initial manuscript submission to ApJ. | qmc_07-03-22.tar.gz |
(2) License
Our code us currently distributed under this licence: Creative Commons Attribution 4.0 International
(3) Installation
To install our QMC code, download, ungzip and untar the latest version, change into the QMC directory and type make:
machine:~/QMC_source_code_03-08-23> make
g++ -O3 -Wall -pedantic -funroll-loops -DRING Standard.C Main.C Form.C Timer.C PrintErrorBar.C -lm -o ring
g++ -O3 -Wall -pedantic -funroll-loops -DHARMONIC Standard.C Main.C Form.C Timer.C PrintErrorBar.C -lm -o harm
g++ -O3 -Wall -pedantic -funroll-loops -DROSENBROCK Standard.C Main.C Form.C Timer.C PrintErrorBar.C -lm -o rosen
which will call Gnu's C++ compiler g++ with the argument -O3 for optimization. The arguments -Wall -pedantic -funroll-loops don't matter. It generates three exectuables ring, harm, and rosen to respectively sample our ring potential, a harmonic potential, and the 2d Rosenbrock density. For details please read our manuscript in ApJ.
If the compilation still fails, try editing the Makefile or switch to a different compiler. We do not provide executables for any operating system here but our source code has been compiled successfully with these compilers:
Linux g++ version 4.8.4 (Ubuntu 4.8.4-2ubuntu1~14.04.4)
Linux g++ version 4.8.5 (Red Hat 4.8.5-44) (GCC)
macOS clang version 14.0.3 (clang-1403.0.22.14.1)
Intel icpc version 2021.6.0
To compile and run our code, you need a C++ compiler. On Macs, we recommend installing XCode with the command line tools. On Windows, please install Cygwin with g++ version 10.2.1 or later.
(3) The following files are included
but all important lines of code are in MC.h and Main.C. To understand the implementation of the QMC method, we recommend opening the file MC.h and reading the function PerformOneQuadraticMonteCarloSweep(...). The most relevant lines of code are shown here in simplied form:
Array1 <S> s = SetUpNStates(nWalkers); // Set up nWalkers different states of type S
for(int iBlock=0; i<nBlocks; iBlock++) { // loop over blocks
for(int iStep=0; i<nStepsPerBlock; iStep++) { // loop over steps
for(int i=0; i<nWalkers; i++) { // try moving every walker once per step
int j,k;
SelectTwoOtherWalkersAtRandom(i,j,k);
const double tj = -1.0;
const double tk = +1.0;
const double ti = SampleT(a); // sample t space
const double tNew = SampleT(a); // sample t space one more time
const double wi = LagrangeInterpolation(tNew,ti,tj,tk);
const double wj = LagrangeInterpolation(tNew,tj,tk,ti);
const double wk = LagrangeInterpolation(tNew,tk,ti,tj);
S sNew = s[0]; // Create new state by coping over an existing one.
for(int d=0; d<nDim; d++) {
sNew[d] = wi*s[i][d] + wj*s[j][d]+ wk*s[k][d]; // set nDim parameters of new state
}
if (sNew.Valid()) { // check if state sNew is valid before calling Evaluate()
sNew.Evaluate(); // Sets the energy sNew.y which defines the state's probability = exp(-y/temp)
double dy = sNew.y - s[i].y; // difference in energy between new and old state
double prob = pow(fabs(wi),nDim) * exp(-dy/temp); // Note |wi|^nDim and Boltzmann factors
bool accept = (prob>Random()); // Random() returns a single random number between 0 and 1.
if (accept) {
for(int d=0; d<nDim; d++) {
s[i][d] = sNew[d]; // copy over state sNew
}
s[i].y = sNew.y; // copy also its energy
}
}
} // look over all walkers
ComputeDifferentEnsembleAverages(s);
} // end of loop over steps
PrintEndOfBlockStatement();
} // end of loop over blocks
PrintEndOfRunStatement();
set index = 58
set T = 0.01
set n = 6
set a = 1.5
harm -affine n=$n a=$a T=${T} nBlocks=100000 > affine${index}_${T}_${n}_${a}.txt &
harm -qmc n=$n a=$a T=${T} nBlocks=100000 > qmcLin${index}_${T}_${n}_${a}.txt &
harm -qmc -Gaussian n=$n a=$a T=${T} nBlocks=100000 > qmcGau${index}_${T}_${n}_${a}.txt &
# Compare the output with the following results. The MC average of energy, E, should be close to 0.5*n*T = 0.03
grep "Fraction= 0.9" *58_*.txt
affine58_0.01_6_1.5.txt: Fraction= 0.9 n= 90000 E= 0.03000173 +- 0.00001369
qmcGau58_0.01_6_1.5.txt: Fraction= 0.9 n= 90000 E= 0.03003602 +- 0.00001169
qmcLin58_0.01_6_1.5.txt: Fraction= 0.9 n= 90000 E= 0.02999435 +- 0.00001152
machine:~/QMC_source_code_03-08-23> tcsh
set index = 57
set T = 0.01
set n = 6
set a = 1.5
set m = 6
set R = 1.0
ring -low -affine m=$m n=$n a=$a T=${T} R=${R} nBlocks=100000 > affine${index}_${T}_${n}_${m}_${a}_${R}.txt &
ring -low -qmc m=$m n=$n a=$a T=${T} R=${R} nBlocks=100000 > qmcLin${index}_${T}_${n}_${m}_${a}_${R}.txt &
ring -low -qmc -Gaussian m=$m n=$n a=$a T=${T} R=${R} nBlocks=100000 > qmcGau${index}_${T}_${n}_${m}_${a}_${R}.txt &
# Compare the output with the following. The MC averages will not agree perfectly.
machine:~/QMC_source_code_03-08-23> grep "Fraction= 0.9" *57_*.txt
affine57_0.01_6_6_1.5_1.0.txt: Fraction= 0.9 n= 90000 E= -0.00031481 +- 0.00007970
qmcGau57_0.01_6_6_1.5_1.0.txt: Fraction= 0.9 n= 90000 E= -0.00030795 +- 0.00004486
qmcLin57_0.01_6_6_1.5_1.0.txt: Fraction= 0.9 n= 90000 E= -0.00026504 +- 0.00003554
machine:~/CMS_MC_test_03-08-23a> tcsh
set index = 199
set T = 1.0
foreach nWalkers (3 4 5 6 8 10 20)
set para = "T=$T nStepsPerBlock=1000 nBlocks=100000 nWalkers=${nWalkers}"
foreach nMovers (3 4 5 6 10)
foreach a (1.2 1.5 2.0 3.0)
rosen -walk $para nMovers=$nMovers a=$a > walk${index}_${nWalkers}_${nMovers}_${a}.txt &
end
end
end
| At the moment, we do not have a Python version of our QMC code but it is high on our to-do list. |
If you have feedback, comments, or a specific scientific problem you would like to solve please send email to militzer[at]berkeley[dot]edu.
Best wishes and happy QMC computation!
Burkhard Militzer
August, 20, 2023.