



Next: Sampling with Open Paths
Up: Path Integral Monte Carlo
Previous: Shock Hugoniot
Contents
Off-Diagonal Density Matrix Elements
In this chapter, we are going to describe the sampling of off-diagonal
matrix elements using the path-integral formalism. Instead of
calculating diagonal density matrix elements
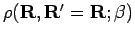 , for which the paths return to their starting
point, we now include the possibility of open paths. Opening one path
allows one the sampling of the single-particle reduced density matrix defined
by,
, for which the paths return to their starting
point, we now include the possibility of open paths. Opening one path
allows one the sampling of the single-particle reduced density matrix defined
by,
![\begin{displaymath}
\rho^{[1]}({\bf r}_1,{\bf r}_1') = \frac{{V^{\!\!\!\!\!\!\:^...
...{\bf r}_N \, , \,{\bf r}_1',{\bf r}_2,\ldots,{\bf r}_N)
\quad,
\end{displaymath}](img973.png) |
(208) |
which is related to the momentum distribution. A PIMC simulation with
two open paths samples the two-particle reduced density matrix,
![\begin{displaymath}
\rho^{[2]}({\bf r}_1,{\bf r}_2,{\bf r}_1',{\bf r}_2') = \fra...
..., , \,{\bf r}_1',{\bf r}_2',{\bf r}_3,\ldots,{\bf r}_N)
\quad,
\end{displaymath}](img974.png) |
(209) |
which will be used to study natural orbitals. In the following
two sections, we discuss the modifications to the sampling procedure
in order to deal with the open ends.
Subsections
Burkhard Militzer
2003-01-15
![]() , for which the paths return to their starting
point, we now include the possibility of open paths. Opening one path
allows one the sampling of the single-particle reduced density matrix defined
by,
, for which the paths return to their starting
point, we now include the possibility of open paths. Opening one path
allows one the sampling of the single-particle reduced density matrix defined
by,