



Next: Natural orbitals
Up: Off-Diagonal Density Matrix Elements
Previous: Nodal Restriction for Open
Contents
Momentum Distribution
In the path integral formalism, the momentum distribution can be
derived by projecting out a many particle state with momentum
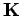 . The projection operator is given by,
. The projection operator is given by,
Applying it to the thermal density matrix using
Eq. 2.7 leads to
 |
(213) |
To find the single particle momentum distribution, one averages over
the momentum of all particles except the first, which is equivalent to
performing the integrals
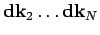 . Including an
extra normalization factor of
. Including an
extra normalization factor of 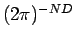 , this leads to the single
particle momentum distribution,
, this leads to the single
particle momentum distribution,
![\begin{displaymath}
n(\mathbf{k}) = (2 \pi)^{-3} \int {\bf d}{\bf r}_1 {\bf d}{\...
...k}({\bf r}'_1-{\bf r}_1)} \; \rho^{[1]}({\bf r}_1,{\bf r}_1'),
\end{displaymath}](img991.png) |
(214) |
where
![$\rho^{[1]}({\bf r}_1,{\bf r}_1')$](img992.png) is the one-particle reduced density
matrix defined in Eq. 5.1. The normalizations are given by
is the one-particle reduced density
matrix defined in Eq. 5.1. The normalizations are given by
![$\int \! {\bf d}{\bf r}\, \rho^{[1]}({\bf r},{\bf r}) = {V^{\!\!\!\!\!\!\:^\diamond}}$](img993.png) and
and
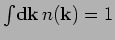 . For isentropic homogeneous systems, the one-particle
reduced density matrix is only a function of
. For isentropic homogeneous systems, the one-particle
reduced density matrix is only a function of
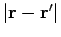 , which
allows one to introduce the function
, which
allows one to introduce the function
![$n(\vert{\bf r}-{\bf r}'\vert)\equiv\rho^{[1]}({\bf r},{\bf r}')$](img996.png) with
with 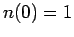 . It represents
the distribution function of the separation of open ends in a PIMC
simulation with one open path.
. It represents
the distribution function of the separation of open ends in a PIMC
simulation with one open path.
Classical particles exhibit the Maxwellian momentum
distribution. Therefore, the single particle density matrix is a
Gaussian,
For an ideal Fermi gas at 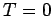 , the momentum distribution is a Fermi function,
, the momentum distribution is a Fermi function,
The single particle density matrix 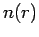 is proportional to the
spherical Bessel function
is proportional to the
spherical Bessel function 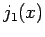 , which oscillates around zero. In
the PIMC simulations,
, which oscillates around zero. In
the PIMC simulations, 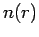 can be obtained in form of a histogram,
in which the separations of the open ends weighted with the sign of the
permutation are entered. At separations
can be obtained in form of a histogram,
in which the separations of the open ends weighted with the sign of the
permutation are entered. At separations 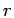 where it is negative, odd
permutations leading negative contributions must outweigh even
permutations making positive contributions.
where it is negative, odd
permutations leading negative contributions must outweigh even
permutations making positive contributions. 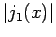 decays slowly
as
decays slowly
as 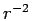 , which requires macroscopic exchange cycles to
occur. Those are solely a consequence of the discontinuity of
, which requires macroscopic exchange cycles to
occur. Those are solely a consequence of the discontinuity of 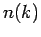 at
at 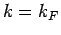 .
.
Before we discuss results from PIMC simulation of interacting systems
we will examine the scaling behavior of the off-diagonal sampling
method. In order to study a certain number of oscillations in 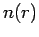 ,
one can make a simple estimation of how many particles are
required. For this purpose, we neglect the fact that Eq. 5.11
was derived in thermodynamic limit,
,
one can make a simple estimation of how many particles are
required. For this purpose, we neglect the fact that Eq. 5.11
was derived in thermodynamic limit, 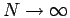 . In a simulation
using a 3D box of size
. In a simulation
using a 3D box of size 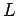 , one can directly measure
, one can directly measure 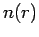 up
to
up
to 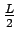 and indirectly up to
and indirectly up to
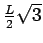 . This leads
to the estimates for the required number of particles given in
Tab. 5.1.
. This leads
to the estimates for the required number of particles given in
Tab. 5.1.
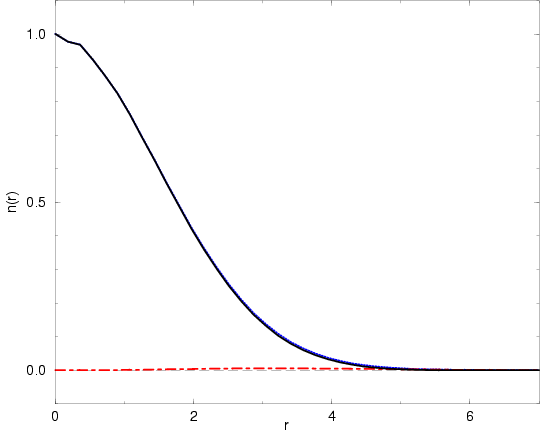
Figure 5.2:
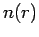 for systems of 33 spin-parallel electrons at
for systems of 33 spin-parallel electrons at
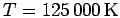 and
and 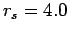 (
(
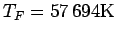 )
(solid line). At this temperature, fermionic effects are only
a small correction to the classical behavior. Therefore
negative contributions (dash-dotted line) are negligible and
the sum of the positive contributions (dotted line) are
almost identical to the full
)
(solid line). At this temperature, fermionic effects are only
a small correction to the classical behavior. Therefore
negative contributions (dash-dotted line) are negligible and
the sum of the positive contributions (dotted line) are
almost identical to the full 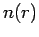 . We also found that the
repulsive interactions do not lead to significant
modification to the non-interacting case given by the
Gaussian function in Eq. 5.9.
. We also found that the
repulsive interactions do not lead to significant
modification to the non-interacting case given by the
Gaussian function in Eq. 5.9.
|
|
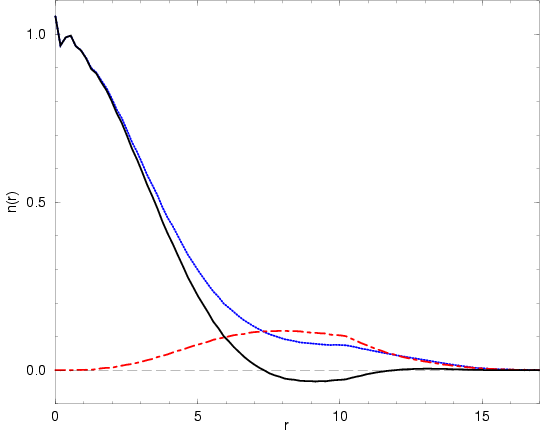
Figure 5.3:
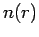 from the system shown in Fig. 5.2 but here for a
significantly lower temperature of
from the system shown in Fig. 5.2 but here for a
significantly lower temperature of
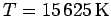 ,
where fermionic effects dominate (
,
where fermionic effects dominate (
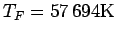 ). This
leads to negative regions in
). This
leads to negative regions in 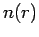 , as expected from the
zero temperature limit given by Eq. 5.11. In these
regions, odd permutations from exchange cycles with an even
number of particles dominate. The functions decrease rapidly
at
, as expected from the
zero temperature limit given by Eq. 5.11. In these
regions, odd permutations from exchange cycles with an even
number of particles dominate. The functions decrease rapidly
at 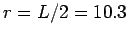 as a result of finite size effects because
the minimum image method is applied.
as a result of finite size effects because
the minimum image method is applied.
|
|
Figure 5.4:
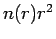 from Fig. 5.2 using the same line styles.
The extra
from Fig. 5.2 using the same line styles.
The extra 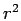 factor emphasizes the small fermionic effects
that lead to some negative contributions.
factor emphasizes the small fermionic effects
that lead to some negative contributions.
|
|
Figure 5.5:
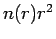 from Fig. 5.3 (thick lines). It shows the
oscillating behavior of n=
from Fig. 5.3 (thick lines). It shows the
oscillating behavior of n=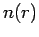 in fermionic systems
(Eq. 5.11). One finds 3 zeros as expected for free
particles (see table 5.1). The thin lines show
finite size corrections for
in fermionic systems
(Eq. 5.11). One finds 3 zeros as expected for free
particles (see table 5.1). The thin lines show
finite size corrections for 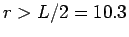 .
.
|
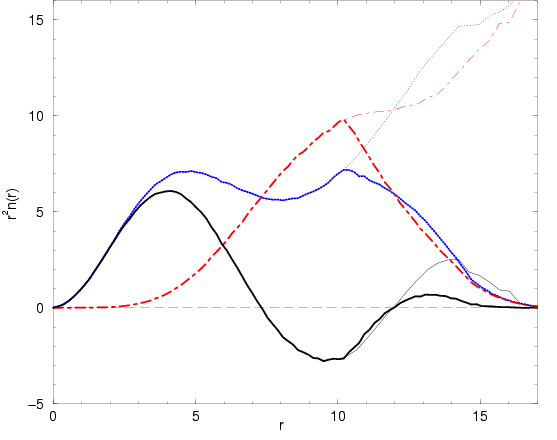
Figure 5.6:
Momentum distribution 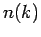 (
( ) for a finite system of 33
spin-parallel electrons at
) for a finite system of 33
spin-parallel electrons at
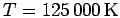 and
and
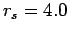 (
(
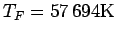 ) also studied in
Fig. 5.2. The
) also studied in
Fig. 5.2. The  symbols show the momentum
distribution for a finite system of non-interacting fermions
under these conditions and the
symbols show the momentum
distribution for a finite system of non-interacting fermions
under these conditions and the  display the
Maxwell-Boltzmann distribution.
display the
Maxwell-Boltzmann distribution.
|
Figure 5.7:
Momentum distribution 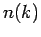 as in Fig. 5.6 but
for a lower temperature of
as in Fig. 5.6 but
for a lower temperature of
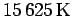 . This leads to
a degenerate Fermi gas described by a Fermi-Dirac
distribution, which is also shown for a system of 33
non-interacting fermions at this
. This leads to
a degenerate Fermi gas described by a Fermi-Dirac
distribution, which is also shown for a system of 33
non-interacting fermions at this 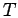 (
( ) and at zero
temperature (solid line). The difference to the
Maxwell-Boltzmann distribution (
) and at zero
temperature (solid line). The difference to the
Maxwell-Boltzmann distribution (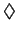 ) is
substantial.
) is
substantial.
|
|
Table 5.1:
Minimal number of particles 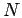 required to observe the
required to observe the 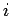 th zero in
the single particle density matrix
th zero in
the single particle density matrix
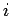 |
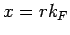 |
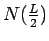 |
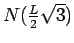 |
| 1 |
4.493 |
12.2 |
2.4 |
| 2 |
7.725 |
62.3 |
12.0 |
| 3 |
10.904 |
175.1 |
33.7 |
| 4 |
14.067 |
376.0 |
72.4 |
From this table, one can quickly realize that the computational
demand grows rapidly with the number of zeros 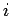 because
because 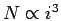 and CPU time
and CPU time
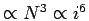 . Furthermore, it should be
noted that one needs to go to sufficiently low temperatures to observe
the fermionic effects and that the CPU time scales linearly with the
number of time slices. Additionally, positive and negative
contributions cancel, which leads to fluctuations in the
observables. The fluctuation do not increase as rapidly as for the
direct fermion method (see section
2.6.5) since we still
use a nodal restriction but one needs converged results from all cycle
lengths, which becomes increasingly difficult at low temperature. A
detailed analysis of the scaling behavior with temperature remains to
be done.
. Furthermore, it should be
noted that one needs to go to sufficiently low temperatures to observe
the fermionic effects and that the CPU time scales linearly with the
number of time slices. Additionally, positive and negative
contributions cancel, which leads to fluctuations in the
observables. The fluctuation do not increase as rapidly as for the
direct fermion method (see section
2.6.5) since we still
use a nodal restriction but one needs converged results from all cycle
lengths, which becomes increasingly difficult at low temperature. A
detailed analysis of the scaling behavior with temperature remains to
be done.
As a first application of the off-diagonal density matrix sampling
method, we chose to study the electron gas because of its
simplicity. The method can be easily extended to hydrogen or
spin-polarized hydrogen. We looked at a system of 33 closed shell
spin-parallel electrons at a density of 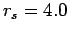 (
(
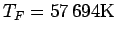 )
and selected the two temperatures
)
and selected the two temperatures 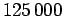 and
and
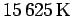 that represent the classical case at high temperature and,
respectively, the degenerate electron gas at low temperature. For
that represent the classical case at high temperature and,
respectively, the degenerate electron gas at low temperature. For
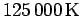 , the observed reduced density matrix
, the observed reduced density matrix 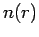 in
Fig. 5.2 is in good approximation the classical Gaussian
function. Due to the high temperature, permutations are relatively
rare. Their contribution can be seen best in Fig. 5.4 where
in
Fig. 5.2 is in good approximation the classical Gaussian
function. Due to the high temperature, permutations are relatively
rare. Their contribution can be seen best in Fig. 5.4 where
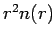 is shown. Since we multiplied by the volume element
is shown. Since we multiplied by the volume element 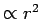 , the graph can be interpreted as the probability of finding the
two ends of the open path separated by
, the graph can be interpreted as the probability of finding the
two ends of the open path separated by 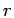 . The corresponding momentum
distribution
. The corresponding momentum
distribution 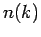 in Fig. 5.6 was calculated directly from
MC average,
in Fig. 5.6 was calculated directly from
MC average,
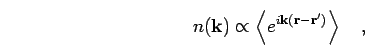 |
(219) |
rather then using a Fourier transform of 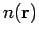 , which would have
required an extrapolation for large
, which would have
required an extrapolation for large 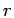 or to store
or to store 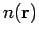 on a 3D
grid because the spherical symmetry is broken by the cubic simulation
box. The observed momentum distribution lies between the
Maxwell-Boltzmann distribution and the Fermi distribution for the
corresponding non-interacting finite system. All three curves are
rather close together because the simulation is performed in a
classical regime. The deviations of the PIMC result from the free
Fermi distribution show the effect of the repulsive interactions
between the electrons, which leads to a depletion of the occupation
probability at small
on a 3D
grid because the spherical symmetry is broken by the cubic simulation
box. The observed momentum distribution lies between the
Maxwell-Boltzmann distribution and the Fermi distribution for the
corresponding non-interacting finite system. All three curves are
rather close together because the simulation is performed in a
classical regime. The deviations of the PIMC result from the free
Fermi distribution show the effect of the repulsive interactions
between the electrons, which leads to a depletion of the occupation
probability at small 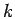 values.
values.
This effect is also present in the low temperature results at
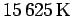 where one finds a degenerate electrons gas. The
momentum distribution in Fig. 5.7 is a Fermi function rather
than a Maxwell-Boltzmann distribution, which can reach arbitrarily
higher occupation for
where one finds a degenerate electrons gas. The
momentum distribution in Fig. 5.7 is a Fermi function rather
than a Maxwell-Boltzmann distribution, which can reach arbitrarily
higher occupation for 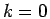 because it is not limited by the Pauli
exclusion principle. The solid line denotes the ideal Fermi gas at
because it is not limited by the Pauli
exclusion principle. The solid line denotes the ideal Fermi gas at
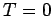 given by Eq. 5.10. Thermal excitations as well as the
Coulomb interaction lead to the population of momentum states above
the ideal Fermi momentum. For interacting systems at
given by Eq. 5.10. Thermal excitations as well as the
Coulomb interaction lead to the population of momentum states above
the ideal Fermi momentum. For interacting systems at 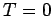 , a
discontinuity in the momentum distribution is still present but some
states are pushed to higher
, a
discontinuity in the momentum distribution is still present but some
states are pushed to higher 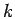 -values (Ortiz and Ballone, 1994). The comparison
with the ideal Fermi gas at
-values (Ortiz and Ballone, 1994). The comparison
with the ideal Fermi gas at 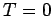 gives an estimate for the thermal
excitations at this temperature. The degree of degeneracy is rather
high, which has a significant consequence for the reduced density
matrix shown in Figs. 5.3 and 5.5. The latter graph
shows how positive contributions dominate at small separations
gives an estimate for the thermal
excitations at this temperature. The degree of degeneracy is rather
high, which has a significant consequence for the reduced density
matrix shown in Figs. 5.3 and 5.5. The latter graph
shows how positive contributions dominate at small separations
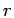 . Then the function goes through zero and even permutations
dominate. After that, it becomes positive again and finally approaches
zero near
. Then the function goes through zero and even permutations
dominate. After that, it becomes positive again and finally approaches
zero near
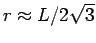 , which is in good agreement with the
estimate given in Tab. 5.1. We corrected for the finite
size effects for
, which is in good agreement with the
estimate given in Tab. 5.1. We corrected for the finite
size effects for 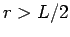 by dividing out the reduction in the volume
element. This correction could also have been done by using the
Fourier transform of the sampled
by dividing out the reduction in the volume
element. This correction could also have been done by using the
Fourier transform of the sampled 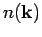 but it would have required
but it would have required
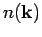 a higher number of k-vectors than we kept. The figure also
shows that the magnitude of the positive and the negative
contributions still grows for
a higher number of k-vectors than we kept. The figure also
shows that the magnitude of the positive and the negative
contributions still grows for
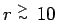 but their difference is
smaller, which leads to the expected decay of
but their difference is
smaller, which leads to the expected decay of 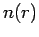 . The reason why
the magnitude of the positive and negative contributions still
increases can be understood from Fig. 5.8 where the
contributions from the individual cycle lengths are shown. Generally,
one finds that cycles of an odd (even) number of particles lead mainly
to positive (negative) contributions despite the possibility that
permutations of nearby closed paths could change the sign since it is
the sign of the total permutation that enters in the average. At small
separations the positive contributions from open 1-cycles
dominate. Two particle permutations give rise to the biggest fraction
of negative contributions for
. The reason why
the magnitude of the positive and negative contributions still
increases can be understood from Fig. 5.8 where the
contributions from the individual cycle lengths are shown. Generally,
one finds that cycles of an odd (even) number of particles lead mainly
to positive (negative) contributions despite the possibility that
permutations of nearby closed paths could change the sign since it is
the sign of the total permutation that enters in the average. At small
separations the positive contributions from open 1-cycles
dominate. Two particle permutations give rise to the biggest fraction
of negative contributions for
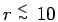 . For
. For
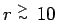 , the
contributions from
, the
contributions from 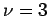 and longer cycles still increase because
the average separation of an open cycle of length
and longer cycles still increase because
the average separation of an open cycle of length 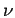 is given by
is given by
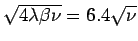 . The cancellation
between odd and even cycles makes the
. The cancellation
between odd and even cycles makes the 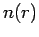 function decay faster
than its positive and negative summands.
function decay faster
than its positive and negative summands.
Figure 5.8:
Distribution 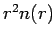 from Fig. 5.5 split into the different
permutation cycles, shown for 1 to 6 particles. Cycles with
an odd number of particles mainly lead to positive
contributions and those even numbers to negative
contributions. The thins lines show the finite size
corrections for
from Fig. 5.5 split into the different
permutation cycles, shown for 1 to 6 particles. Cycles with
an odd number of particles mainly lead to positive
contributions and those even numbers to negative
contributions. The thins lines show the finite size
corrections for 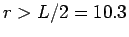 . The figure shows how the
distribution of the different cycles in the restricted path
integral method lead to the oscillations in the
. The figure shows how the
distribution of the different cycles in the restricted path
integral method lead to the oscillations in the 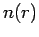 function at sufficiently low
function at sufficiently low 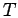 .
.
|
|




Next: Natural orbitals
Up: Off-Diagonal Density Matrix Elements
Previous: Nodal Restriction for Open
Contents
Burkhard Militzer
2003-01-15
![]() . The projection operator is given by,
. The projection operator is given by,
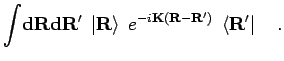

![\begin{displaymath}
n(\mathbf{k}) = (2 \pi)^{-3} \int {\bf d}{\bf r}_1 {\bf d}{\...
...k}({\bf r}'_1-{\bf r}_1)} \; \rho^{[1]}({\bf r}_1,{\bf r}_1'),
\end{displaymath}](img991.png)
![]() ,
one can make a simple estimation of how many particles are
required. For this purpose, we neglect the fact that Eq. 5.11
was derived in thermodynamic limit,
,
one can make a simple estimation of how many particles are
required. For this purpose, we neglect the fact that Eq. 5.11
was derived in thermodynamic limit, ![]() . In a simulation
using a 3D box of size
. In a simulation
using a 3D box of size ![]() , one can directly measure
, one can directly measure ![]() up
to
up
to ![]() and indirectly up to
and indirectly up to
![]() . This leads
to the estimates for the required number of particles given in
Tab. 5.1.
. This leads
to the estimates for the required number of particles given in
Tab. 5.1.



![]() (
(
![]() )
and selected the two temperatures
)
and selected the two temperatures ![]() and
and
![]() that represent the classical case at high temperature and,
respectively, the degenerate electron gas at low temperature. For
that represent the classical case at high temperature and,
respectively, the degenerate electron gas at low temperature. For
![]() , the observed reduced density matrix
, the observed reduced density matrix ![]() in
Fig. 5.2 is in good approximation the classical Gaussian
function. Due to the high temperature, permutations are relatively
rare. Their contribution can be seen best in Fig. 5.4 where
in
Fig. 5.2 is in good approximation the classical Gaussian
function. Due to the high temperature, permutations are relatively
rare. Their contribution can be seen best in Fig. 5.4 where
![]() is shown. Since we multiplied by the volume element
is shown. Since we multiplied by the volume element ![]() , the graph can be interpreted as the probability of finding the
two ends of the open path separated by
, the graph can be interpreted as the probability of finding the
two ends of the open path separated by ![]() . The corresponding momentum
distribution
. The corresponding momentum
distribution ![]() in Fig. 5.6 was calculated directly from
MC average,
in Fig. 5.6 was calculated directly from
MC average,
![]() where one finds a degenerate electrons gas. The
momentum distribution in Fig. 5.7 is a Fermi function rather
than a Maxwell-Boltzmann distribution, which can reach arbitrarily
higher occupation for
where one finds a degenerate electrons gas. The
momentum distribution in Fig. 5.7 is a Fermi function rather
than a Maxwell-Boltzmann distribution, which can reach arbitrarily
higher occupation for ![]() because it is not limited by the Pauli
exclusion principle. The solid line denotes the ideal Fermi gas at
because it is not limited by the Pauli
exclusion principle. The solid line denotes the ideal Fermi gas at
![]() given by Eq. 5.10. Thermal excitations as well as the
Coulomb interaction lead to the population of momentum states above
the ideal Fermi momentum. For interacting systems at
given by Eq. 5.10. Thermal excitations as well as the
Coulomb interaction lead to the population of momentum states above
the ideal Fermi momentum. For interacting systems at ![]() , a
discontinuity in the momentum distribution is still present but some
states are pushed to higher
, a
discontinuity in the momentum distribution is still present but some
states are pushed to higher ![]() -values (Ortiz and Ballone, 1994). The comparison
with the ideal Fermi gas at
-values (Ortiz and Ballone, 1994). The comparison
with the ideal Fermi gas at ![]() gives an estimate for the thermal
excitations at this temperature. The degree of degeneracy is rather
high, which has a significant consequence for the reduced density
matrix shown in Figs. 5.3 and 5.5. The latter graph
shows how positive contributions dominate at small separations
gives an estimate for the thermal
excitations at this temperature. The degree of degeneracy is rather
high, which has a significant consequence for the reduced density
matrix shown in Figs. 5.3 and 5.5. The latter graph
shows how positive contributions dominate at small separations
![]() . Then the function goes through zero and even permutations
dominate. After that, it becomes positive again and finally approaches
zero near
. Then the function goes through zero and even permutations
dominate. After that, it becomes positive again and finally approaches
zero near
![]() , which is in good agreement with the
estimate given in Tab. 5.1. We corrected for the finite
size effects for
, which is in good agreement with the
estimate given in Tab. 5.1. We corrected for the finite
size effects for ![]() by dividing out the reduction in the volume
element. This correction could also have been done by using the
Fourier transform of the sampled
by dividing out the reduction in the volume
element. This correction could also have been done by using the
Fourier transform of the sampled ![]() but it would have required
but it would have required
![]() a higher number of k-vectors than we kept. The figure also
shows that the magnitude of the positive and the negative
contributions still grows for
a higher number of k-vectors than we kept. The figure also
shows that the magnitude of the positive and the negative
contributions still grows for
![]() but their difference is
smaller, which leads to the expected decay of
but their difference is
smaller, which leads to the expected decay of ![]() . The reason why
the magnitude of the positive and negative contributions still
increases can be understood from Fig. 5.8 where the
contributions from the individual cycle lengths are shown. Generally,
one finds that cycles of an odd (even) number of particles lead mainly
to positive (negative) contributions despite the possibility that
permutations of nearby closed paths could change the sign since it is
the sign of the total permutation that enters in the average. At small
separations the positive contributions from open 1-cycles
dominate. Two particle permutations give rise to the biggest fraction
of negative contributions for
. The reason why
the magnitude of the positive and negative contributions still
increases can be understood from Fig. 5.8 where the
contributions from the individual cycle lengths are shown. Generally,
one finds that cycles of an odd (even) number of particles lead mainly
to positive (negative) contributions despite the possibility that
permutations of nearby closed paths could change the sign since it is
the sign of the total permutation that enters in the average. At small
separations the positive contributions from open 1-cycles
dominate. Two particle permutations give rise to the biggest fraction
of negative contributions for
![]() . For
. For
![]() , the
contributions from
, the
contributions from ![]() and longer cycles still increase because
the average separation of an open cycle of length
and longer cycles still increase because
the average separation of an open cycle of length ![]() is given by
is given by
![]() . The cancellation
between odd and even cycles makes the
. The cancellation
between odd and even cycles makes the ![]() function decay faster
than its positive and negative summands.
function decay faster
than its positive and negative summands.
![\includegraphics[angle=270,width=10.0cm]{figures5/J078_nr_c_06.eps}](J078_nr_c_06.png)