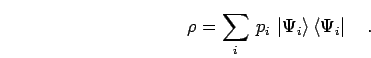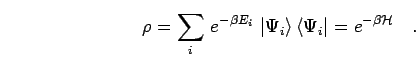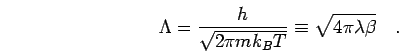Next: Imaginary Time Path Integrals
Up: Path Integral Monte Carlo
Previous: Path Integral Monte Carlo
Contents
A quantum mechanical system in a pure state can be described by single
wave function
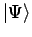 , which can be expressed in terms
of eigenvalues
, which can be expressed in terms
of eigenvalues 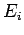 and eigenfunctions
and eigenfunctions
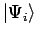 of the
Hamiltonian
of the
Hamiltonian 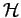 . The corresponding density matrix operator is given by,
. The corresponding density matrix operator is given by,
 |
(10) |
The density matrix provides a convenient way to extend the study to
finite temperature. Following the principles of statistical mechanics,
one puts the system in contact with a heat bath and assigns classical
probabilities 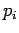 to the quantum mechanical states
to the quantum mechanical states
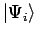 , which leads to a thermal density matrix,
, which leads to a thermal density matrix,
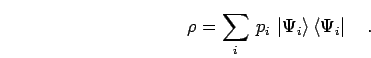 |
(11) |
In the canonical ensemble at temperature 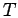 , the probabilities are
proportional to the Boltzmann factor
, the probabilities are
proportional to the Boltzmann factor
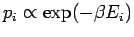 , where
, where
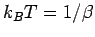 . The density matrix now reads,
. The density matrix now reads,
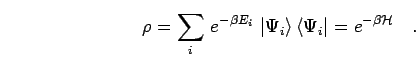 |
(12) |
The expectation of any operator 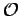 is given by,
is given by,
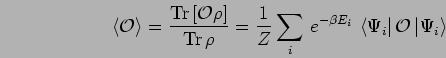 |
(13) |
and the canonical partition function is
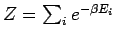 . For sake of numerical simulations, it is convenient to change to a
position-space representation. Introducing the set of coordinates for
a system of
. For sake of numerical simulations, it is convenient to change to a
position-space representation. Introducing the set of coordinates for
a system of 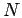 particles in
particles in 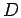 dimensions
dimensions
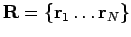 , the density matrix becomes,
, the density matrix becomes,
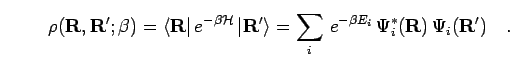 |
(14) |
For any hermitian Hamiltonian 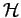 the density matrix is symmetric in its two arguments,
the density matrix is symmetric in its two arguments,
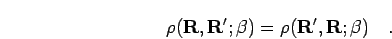 |
(15) |
The expectation value is given by,
For a free particle in a periodically repeated box of size 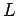 and volume
and volume
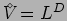 , the
density matrix can derived from the exact eigenfunctions of the
Hamiltonian given by plane waves,
, the
density matrix can derived from the exact eigenfunctions of the
Hamiltonian given by plane waves,
 |
(18) |
with k-vector
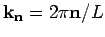 , where
, where  is a
is a  -dimensional integer vector. Hence,
-dimensional integer vector. Hence,
where
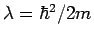 for a particle of mass
for a particle of mass
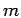 . Alternatively, this solution can be derived from the Bloch
equation,
. Alternatively, this solution can be derived from the Bloch
equation,
 |
(22) |
which is a diffusion equation in imaginary time  . The initial condition
is provided by the known high temperature limit,
. The initial condition
is provided by the known high temperature limit,
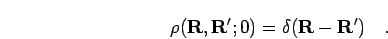 |
(23) |
For free particles, the Bloch equation simply reads,
 |
(24) |
The 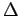 operator can be applied either to the first or to the
second argument in
operator can be applied either to the first or to the
second argument in
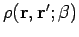 . In any case, this equation
describes the diffusion of paths in imaginary time. The exact solution
is given by Eq. 2.11. The diffusion constant
. In any case, this equation
describes the diffusion of paths in imaginary time. The exact solution
is given by Eq. 2.11. The diffusion constant
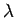 is determined by the mass of the particle. It is large for
light particles leading to a fast diffusion in imaginary time, and
small for heavy and therefore classical particles. The width of the
density matrix is given by
is determined by the mass of the particle. It is large for
light particles leading to a fast diffusion in imaginary time, and
small for heavy and therefore classical particles. The width of the
density matrix is given by
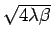 , which is related to the frequently used
thermal de Broglie wave length defined as,
, which is related to the frequently used
thermal de Broglie wave length defined as,
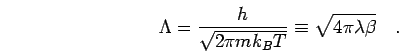 |
(25) |
If this length reaches the order of the inter-particle spacing, many
body quantum effects become important. This relation is usually
discussed in terms of the degeneracy parameter,
 |
(26) |
which relates the volume per particle
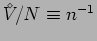 to the
volume occupied by an individual path
to the
volume occupied by an individual path 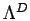 . This parameter
defines a temperature scale for the emergence of quantum statistical
effects such as Bose condensation in Bosonic systems and the formation
of a Fermi surface in Fermion systems. The latter process will be
discussed in detail in sections
2.6 and
5.3.
. This parameter
defines a temperature scale for the emergence of quantum statistical
effects such as Bose condensation in Bosonic systems and the formation
of a Fermi surface in Fermion systems. The latter process will be
discussed in detail in sections
2.6 and
5.3.




Next: Imaginary Time Path Integrals
Up: Path Integral Monte Carlo
Previous: Path Integral Monte Carlo
Contents
Burkhard Militzer
2003-01-15
![]() , which can be expressed in terms
of eigenvalues
, which can be expressed in terms
of eigenvalues ![]() and eigenfunctions
and eigenfunctions
![]() of the
Hamiltonian
of the
Hamiltonian ![]() . The corresponding density matrix operator is given by,
. The corresponding density matrix operator is given by,