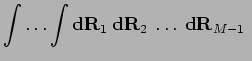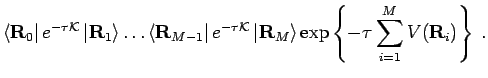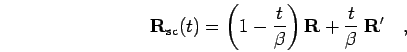Next: Pair Density Matrix
Up: Path Integral Monte Carlo
Previous: The Thermal Density Matrix
Contents
The underlying principle for the introduction of path integrals in
imaginary time is the product property of the density matrix stating
that the low temperature density matrix can be expressed as a product
of high temperature matrices. In operator notation this reads,
 |
(27) |
where the time step is
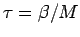 . In position space
this becomes a convolution, in which one has to integrate over all
intermediate time slices,
. In position space
this becomes a convolution, in which one has to integrate over all
intermediate time slices,
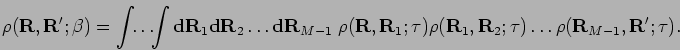 |
(28) |
This is called a path integral in imaginary time. The expression is
exact for any 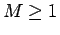 . In the limit
. In the limit 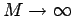 , it becomes
a continuous paths beginning at
, it becomes
a continuous paths beginning at 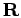 and ending at
and ending at 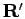 .
.
The reason for using a path integral is in the limit of high
temperature, the density matrix can be calculated. Usually the
Hamiltonian can be split in a kinetic and in a potential part,
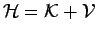 and the density matrix can expressed using the following
operator identity (Raedt and Raedt, 1983),
and the density matrix can expressed using the following
operator identity (Raedt and Raedt, 1983),
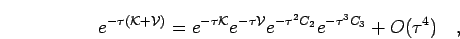 |
(29) |
where
![\begin{displaymath}
C_2 = \left[ A,B\right] /2
\quad,\quad\quad\quad\quad\quad\quad\quad
\end{displaymath}](img273.png) |
(30) |
and
![\begin{displaymath}
C_3 = \left[ \left[ B,A\right],A+2B\right] /6\quad\quad\quad
\quad.
\end{displaymath}](img274.png) |
(31) |
In the limit of 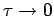 , one can neglect the commutators, which
are of higher order in
, one can neglect the commutators, which
are of higher order in 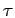 . This is known as the primitive
approximation,
. This is known as the primitive
approximation,
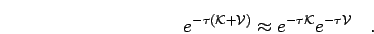 |
(32) |
It states that in the limit of 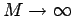 , the density matrix can
be written as product of a potential and kinetic density matrix. This
has been shown by Trotter (1959),
, the density matrix can
be written as product of a potential and kinetic density matrix. This
has been shown by Trotter (1959),
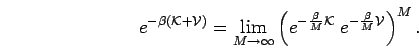 |
(33) |
The density matrix for a system of 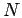 particles in the primitive
approximation is given by,
particles in the primitive
approximation is given by,
In the path integral formalism this is written as,
![\begin{displaymath}
\rho({\bf R},{\bf R}'; \beta) =
\! \! \! \int \limits_{{\bf...
... }
\! \! \! \! {\bf d}{\bf R}_t \;\; e^{-S[{\bf R}_t] }\quad,
\end{displaymath}](img281.png) |
(35) |
where ![$S[{\bf R}_t]$](img282.png) is the action of the path. Alternatively, one
separates the kinetic and potential parts,
is the action of the path. Alternatively, one
separates the kinetic and potential parts,
The free particle terms act like a
weight over all Brownian random walks (BRW) in imaginary time 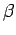 starting at
starting at 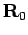 and ending at
and ending at 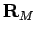 . In the limit of
. In the limit of 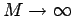 , this leads to the
Feynman-Kac relation
, this leads to the
Feynman-Kac relation
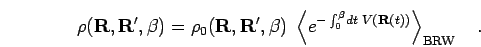 |
(36) |
In the semi-classical approximation, one considers only the
classical path,
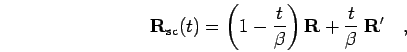 |
(37) |
instead of integrating over all BRW. The resulting semi-classical
density matrix reads,
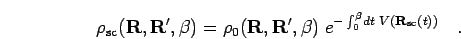 |
(38) |
Already, the primitive approximation is a sufficient basis for a path
integral Monte Carlo simulation. However, the required number of time
slices to reach accurate results would be enormous. The following
sections, we discuss methods to derive a more accurate high
temperature density matrix in order to reduce the number of slices to
a computationally feasible level. A pair action will be derived, which
contains the exact solution of the two particle problem. This means
only one time slice is required for a simulation of two particles at
any temperature. However, in many particle systems, a path integral is
needed because of many-particle effects and the fermion nodes, which
will be discussed in section 2.6.




Next: Pair Density Matrix
Up: Path Integral Monte Carlo
Previous: The Thermal Density Matrix
Contents
Burkhard Militzer
2003-01-15
![]() and the density matrix can expressed using the following
operator identity (Raedt and Raedt, 1983),
and the density matrix can expressed using the following
operator identity (Raedt and Raedt, 1983),
![\begin{displaymath}
\rho({\bf R},{\bf R}'; \beta) =
\! \! \! \int \limits_{{\bf...
... }
\! \! \! \! {\bf d}{\bf R}_t \;\; e^{-S[{\bf R}_t] }\quad,
\end{displaymath}](img281.png)