For the systems under study, the interactions consist of pairwise
additive potentials,
![]() . The
full density matrix given by the Feynman-Kac relation,
. The
full density matrix given by the Feynman-Kac relation,
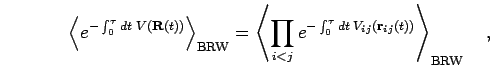 |
(39) |
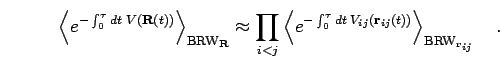 |
(40) |
Electrons and protons interact via the Coulomb potential. For the two
particle problem, the eigenfunctions of the Hamiltonian can be
expressed in terms of special functions and the pair density matrix
can be calculated by performing the sum over all states
(Pollock, 1988). However, the states are only known analytically in an
infinite volume. For the purpose of a simulation in a periodic cell,
the Coulomb potential is broken up into a short range part in real
space and a long range part in ![]() -space using an optimized Ewald
break-up (Ewald, 1917) developed by
(Natoli and Ceperley, 1995). For both parts separately, a pair action will be derived
as discussed in the following sections. It should be noted that the
break up of the potential is an approximation, which is made in order
to calculate the pair density matrix corresponding to a long-range
pair potential in a periodic system. Ideally, one would calculate the
full action and then perform an Ewald break-up.
-space using an optimized Ewald
break-up (Ewald, 1917) developed by
(Natoli and Ceperley, 1995). For both parts separately, a pair action will be derived
as discussed in the following sections. It should be noted that the
break up of the potential is an approximation, which is made in order
to calculate the pair density matrix corresponding to a long-range
pair potential in a periodic system. Ideally, one would calculate the
full action and then perform an Ewald break-up.