Next: Path Integrals for Fermions
Up: Pair Density Matrix
Previous: Short Range Action
Contents
The long range part of the potential leads to long range action. As a
first step, it can be calculated from the primitive approximations as
used in (Shumway, 1999). Alternatively, one can use the random phase
approximation (RPA) (Pines and Nozieres, 1989) to obtain an improved long range
action (for details see (Magro, 1996)), which is constructed in such
a way that the local energy is minimized,
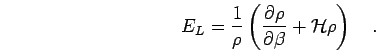 |
(48) |
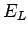 vanishes for a solution of the Bloch equation 2.13. One
assumes a given short range density matrix
vanishes for a solution of the Bloch equation 2.13. One
assumes a given short range density matrix 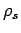 , which solves the
Bloch equation for the Hamiltonian
, which solves the
Bloch equation for the Hamiltonian
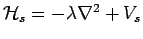 .
For the full Hamiltonian
.
For the full Hamiltonian
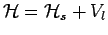 with the additional
potential
with the additional
potential 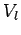 , one derives a long range density matrix
, one derives a long range density matrix 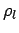 such
that the density matrix
such
that the density matrix 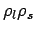 leads to
leads to 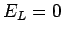 . One writes the
long range potential
. One writes the
long range potential 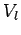 and action
and action 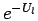 in the form,
in the form,
where
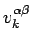 is the Fourier transform of the potential
between particle of type
is the Fourier transform of the potential
between particle of type 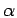 and
and 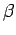 denoted by T
denoted by T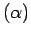 and
T
and
T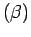 . Setting
. Setting 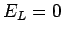 , leads to three body terms, which are
approximated by the RPA. The resulting first order differential
equations, which are integrated numerically in imaginary time from
, leads to three body terms, which are
approximated by the RPA. The resulting first order differential
equations, which are integrated numerically in imaginary time from 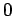 to
to 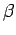 with the initial condition
with the initial condition 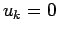 . The calculated
coefficients
. The calculated
coefficients 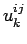 then enter PIMC simulations as long range
action in form of Eq. 2.42.
then enter PIMC simulations as long range
action in form of Eq. 2.42.




Next: Path Integrals for Fermions
Up: Pair Density Matrix
Previous: Short Range Action
Contents
Burkhard Militzer
2003-01-15