



Next: Monte Carlo Sampling
Up: Path Integral Monte Carlo
Previous: Long Range Action
Contents
According to the spin-statistics theorem, fermion systems are
described by totally antisymmetric wave functions and bosonic systems
by symmetric ones. In other words, the wave functions must be
antisymmetric/symmetric under the exchange of two identical particles,
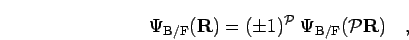 |
(53) |
where 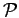 stands for any of the
stands for any of the 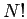 permutations of the particle
label in the many-body coordinate
permutations of the particle
label in the many-body coordinate 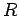 . In systems with additional
internal degrees of freedom such as spin, the permutation is applied
to those as well. The
. In systems with additional
internal degrees of freedom such as spin, the permutation is applied
to those as well. The 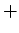 sign corresponds bosonic systems (B) and the
sign corresponds bosonic systems (B) and the
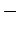 sign to fermionic systems (F). This symmetry property can be
realized by applying an antisymmetrization/symmetrization operator to
a wave function for distinguishable particles
sign to fermionic systems (F). This symmetry property can be
realized by applying an antisymmetrization/symmetrization operator to
a wave function for distinguishable particles
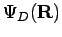 ,
,
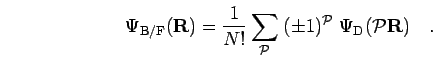 |
(54) |
The density matrix for a fermion/bosonic system is constructed
from these states and can be written as,
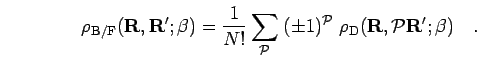 |
(55) |
One can (anti)symmetrize with respect to the first or second argument
or both. All three ways are equivalent and lead to the same physical
observables. The (anti)symmetry enters into the path integral
formalism as a sum over all 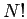 permutations. In addition to the
integral over all configurations of paths, one has to sum over possible
permutations of final set of coordinates
permutations. In addition to the
integral over all configurations of paths, one has to sum over possible
permutations of final set of coordinates
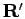 . Eq. 2.19 then reads,
. Eq. 2.19 then reads,
The 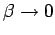 limit from Eq. 2.14 now becomes,
limit from Eq. 2.14 now becomes,
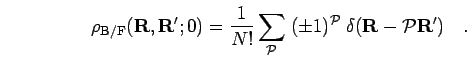 |
(58) |
In most applications, one uses the path integrals to calculate averages
from Eq. 2.7. There one needs the trace of the
density matrix, which means one sums up all closed paths (for
sampling with open paths see chapter 5). For
distinguishable particles, they start at any 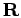 and return to
it. For fermions and bosons one also sums over paths that return to a
permuted set of coordinates given by
and return to
it. For fermions and bosons one also sums over paths that return to a
permuted set of coordinates given by
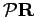 . Those contributions
become relevant if the degeneracy parameter (Eq. 2.17) is
the order of 1 or greater.
. Those contributions
become relevant if the degeneracy parameter (Eq. 2.17) is
the order of 1 or greater.
The path integral technique has been applied extensively to bosonic
systems in particular to liquid  He (Ceperley, 1995; Grüter et al., 1997). It is an
exact method because all permutations carry the same sign and one does
not have to deal with cancellation effects of positive and negative
contributions as in fermionic systems. Those will be discussed in section
2.6. We call a method exact (see (Ceperley, 1996)),
if it only contains approximations, which can be controlled by an
adjustable parameter, and therefore converges to the exact numerical
results with increasing accuracy.
He (Ceperley, 1995; Grüter et al., 1997). It is an
exact method because all permutations carry the same sign and one does
not have to deal with cancellation effects of positive and negative
contributions as in fermionic systems. Those will be discussed in section
2.6. We call a method exact (see (Ceperley, 1996)),
if it only contains approximations, which can be controlled by an
adjustable parameter, and therefore converges to the exact numerical
results with increasing accuracy.




Next: Monte Carlo Sampling
Up: Path Integral Monte Carlo
Previous: Long Range Action
Contents
Burkhard Militzer
2003-01-15
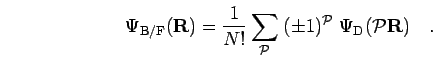
![]() He (Ceperley, 1995; Grüter et al., 1997). It is an
exact method because all permutations carry the same sign and one does
not have to deal with cancellation effects of positive and negative
contributions as in fermionic systems. Those will be discussed in section
2.6. We call a method exact (see (Ceperley, 1996)),
if it only contains approximations, which can be controlled by an
adjustable parameter, and therefore converges to the exact numerical
results with increasing accuracy.
He (Ceperley, 1995; Grüter et al., 1997). It is an
exact method because all permutations carry the same sign and one does
not have to deal with cancellation effects of positive and negative
contributions as in fermionic systems. Those will be discussed in section
2.6. We call a method exact (see (Ceperley, 1996)),
if it only contains approximations, which can be controlled by an
adjustable parameter, and therefore converges to the exact numerical
results with increasing accuracy.