The two particle density matrix is of particular relevance for the understanding of quantum-mechanical many body systems. It contains more information than can be extracted from diagonal density matrix elements only and can be used to study eigenstates, their energies and the thermal excitations in the system. It is important for the characterization of the electronic excitations in the hydrogen plasma. In principle, one can determine the different electronic states and calculate the occupation probabilities. These are important for the radiative properties of the plasma and allow one to calculate absorption and emission spectra. The purpose of the following calculation is to determine the electronic excitations from a first principles calculation, which can then enter subsequent plasma models as an alternative to results from chemical models, in which the occupation numbers are estimated from the chemical equilibrium of approximately known eigenstates.
Furthermore, one would like to have a way to distinguish between free and bound states. This information can be used to estimate dynamic properties such as the conductivity. However, it has been proven to be a challenging task to give a rigorous and also practical criterion for the definition of free and bound states. In our approach, we followed the ideas of Girardeau (1990), who suggested the use of the two particle density matrix. Its eigenvalues are related to the occupation number and its eigenvector are called natural orbitals. They are of particular importance for configuration interaction methods in quantum chemistry because they lead to the fastest convergence (Szabo and Ostlund, 1996).
The two particle density matrix as defined in Eq. 5.2 requires
path integral simulations with two open paths, which can be either of
the same or of different particle type. One introduces relative and
center-of-mass coordinates,
![]() and
and
![]() . In a translationally invariant
system, the pair matrix depends only on the separation of
. In a translationally invariant
system, the pair matrix depends only on the separation of
![]() ,
,
| (220) |
![\begin{displaymath}
\rho^{[2]}_\mathbf{k}({\bf r},{\bf r}') = \int_{V^{\!\!\!\!\...
...m cm}}} \rho^{[2]}({\bf r},{\bf r}',{\bf r}_{{\rm cm}})
\quad.
\end{displaymath}](img1042.png) |
(221) |
In this approach, we did not make a distinction between the discrete
spectrum of bound states and the continuum of free states. Both are
included in the sum of Eq. 5.16. Since we applied this
method to PIMC simulations in a finite volume, free states will
have a discrete spectrum as well. In the simulation, one calculates the
two particle density matrix from the following by average,
| (226) |
 |
(227) |
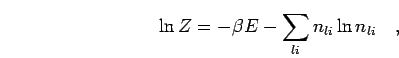 |
(228) |
This off-diagonal sampling method can be applied to different regimes in hydrogen. One can determine the electronic excitations in atoms by opening an electron and a proton path. A pair of open proton paths can be used to study the formation of hydrogen molecules. The eigenvectors then correspond to different rotational and vibrational excitations. In the following sections, we show how this method can be applied in PIMC simulations and show preliminary results for the electronic excitations in hydrogen.