|

|
| Method | 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f |
| A | 0.535 | 0.056 | 0.049 | 0.042 | 0.036 | 0.032 | 0.027 | 0.022 | 0.019 | 0.017 |
| B | 0.973 | 0.009 | 0.003 | 0.002 | 0.002 | 0.002 | 0.000 | 0.000 | 0.000 | 0.007 |
| C | 0.919 | 0.012 | 0.010 | 0.006 | 0.008 | 0.008 | 0.003 | 0.002 | 0.003 | 0.006 |
In an off-diagonal PIMC simulation of spin-polarized hydrogen, there
are ![]() protons,
protons, ![]() closed electron paths and one open electron
path that can be permuted with the others electrons. The simplest
approach to generalize the natural orbital method to systems with
several protons would be to loop over all protons
closed electron paths and one open electron
path that can be permuted with the others electrons. The simplest
approach to generalize the natural orbital method to systems with
several protons would be to loop over all protons ![]() and
to add all pairs of
and
to add all pairs of
![]() to the
to the ![]() matrices. Then the analysis proceeds like in the case of
the single hydrogen atom. The result for a system of 32 protons and
spin-polarized electrons at
matrices. Then the analysis proceeds like in the case of
the single hydrogen atom. The result for a system of 32 protons and
spin-polarized electrons at
![]() and
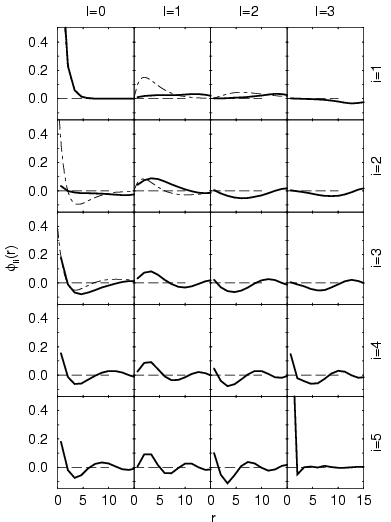
and ![]() is shown in
Fig. 5.11. We chose to study a system of electrons in the
same spin state, which prevents the formation of molecules and
simplifies the following analysis. Under this condition, one expects
the electrons mainly to be in the 1s ground state at one of the protons
because the ideal Saha equation predicts an occupation probability of
0.9998 for the ground state. However, the described analysis
procedure (eigenvectors in Fig. 5.11 and occupation
numbers in Tab. 5.2) does not reproduce this result. Instead,
it leads to a far too low occupation of 0.535 and one finds a
significant contribution from higher
is shown in
Fig. 5.11. We chose to study a system of electrons in the
same spin state, which prevents the formation of molecules and
simplifies the following analysis. Under this condition, one expects
the electrons mainly to be in the 1s ground state at one of the protons
because the ideal Saha equation predicts an occupation probability of
0.9998 for the ground state. However, the described analysis
procedure (eigenvectors in Fig. 5.11 and occupation
numbers in Tab. 5.2) does not reproduce this result. Instead,
it leads to a far too low occupation of 0.535 and one finds a
significant contribution from higher ![]() components. These
contributions can be interpreted as an artifact of this analysis
procedure, in which we averaged over all protons, as can be understood
from the following argument. If one imagines the electron fixed in the
1s state at proton 1 the pairs of
components. These
contributions can be interpreted as an artifact of this analysis
procedure, in which we averaged over all protons, as can be understood
from the following argument. If one imagines the electron fixed in the
1s state at proton 1 the pairs of
![]() from another distant proton always give a
small angle
from another distant proton always give a
small angle ![]() . The distribution of the angles
. The distribution of the angles ![]() is very
non-uniform since it is localized around
is very
non-uniform since it is localized around ![]() . Therefore those
contributions cannot be expressed as an s state.
. Therefore those
contributions cannot be expressed as an s state.