



Next: Antisymmetry in the Parameter
Up: Variational Density Matrix Technique
Previous: Thermodynamic Estimators
Contents
We represent the many-particle density matrix by a determinant of
one-particle density matrices (Eq. 3.79). It can written as,
where a factor 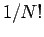 was dropped.
The permutation sum is over all permutations
of identical particles (e.g. same spin (
was dropped.
The permutation sum is over all permutations
of identical particles (e.g. same spin (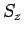 ) electrons) and the permutation
signature
) electrons) and the permutation
signature
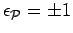 .
The initial conditions for Eq. 3.19
are
.
The initial conditions for Eq. 3.19
are 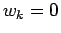 ,
,
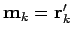 , and
, and 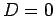 .
For this ansatz the generator of the norm matrix, Eq. 3.22 is,
.
For this ansatz the generator of the norm matrix, Eq. 3.22 is,
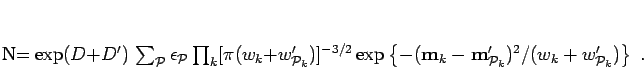 |
(176) |
For a periodic system the above equation is also summed over all periodic
simulation cell vectors, 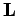 , with
, with
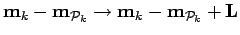 .
If only the identity permutation is considered the norm matrix
is easily inverted so that Eq. 3.19 gives
.
If only the identity permutation is considered the norm matrix
is easily inverted so that Eq. 3.19 gives
For systems of electrons and ions the full expression for 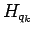 and the norm
matrix are derived in App. A.
and the norm
matrix are derived in App. A.
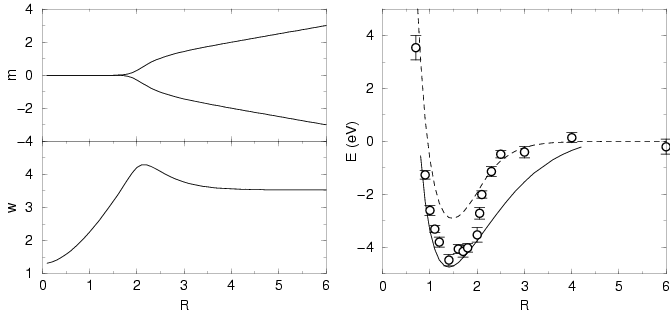
Figure 3.3:
Gaussian approximation for the ground state of a hydrogen
molecule for bond length 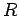 . The top left panel shows the Gaussian
mean parameter
. The top left panel shows the Gaussian
mean parameter 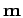 for the two electrons. These stay in
the center of the bond (
for the two electrons. These stay in
the center of the bond (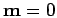 ) until about
) until about 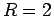 and then
attach themselves to the separating protons (
and then
attach themselves to the separating protons (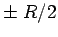 ). The width
parameter, displayed in the lower left panel, makes the transition from
the optimal value for a helium atom,
). The width
parameter, displayed in the lower left panel, makes the transition from
the optimal value for a helium atom, 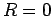 , to the hydrogen atom
result
, to the hydrogen atom
result 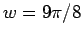 at large
at large 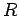 . The right panel shows the dissociation
energy for the singlet state computed from
Eq. 3.49 (open circles with error bars) and the
thermodynamic estimator (
. The right panel shows the dissociation
energy for the singlet state computed from
Eq. 3.49 (open circles with error bars) and the
thermodynamic estimator (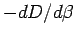 ) (dashed line) compared
to the exact results of Kolos and Roothan (solid line).
) (dashed line) compared
to the exact results of Kolos and Roothan (solid line).
|
|
Application to an isolated hydrogen molecule at low temperature is
shown in Figure 3.3. This is for the singlet state
(anti-parallel electron spins). The triplet state is considered later
after a discussion of how to treat permutation terms in the parameter
equations. The bond length at minimum energy is 1.47, compared with
the experimental value of 1.40. The direct energy estimator
Eq. 3.49 gives a dissociation energy of 4.50 eV at the
minimum compared to the experimental value of 4.75 eV. Beyond 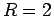 ,
the energy rises quickly toward the value given by the Rayleigh-Ritz
estimator
,
the energy rises quickly toward the value given by the Rayleigh-Ritz
estimator 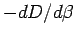 .
.




Next: Antisymmetry in the Parameter
Up: Variational Density Matrix Technique
Previous: Thermodynamic Estimators
Contents
Burkhard Militzer
2003-01-15
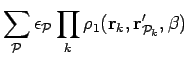
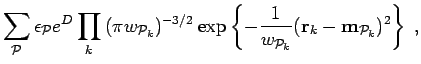
![]() ,
the energy rises quickly toward the value given by the Rayleigh-Ritz
estimator
,
the energy rises quickly toward the value given by the Rayleigh-Ritz
estimator ![]() .
.