



Next: Thermodynamic Estimators
Up: Variational Density Matrix Properties
Previous: Zero Temperature Limit
Contents
Loss of Symmetry
The exact density matrix is symmetric under
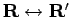 .
Since we have singled out
.
Since we have singled out 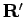 as the initial point for the
imaginary time dynamics, it is not clear that the approximation given
in Eq. 3.27 automatically satisfies this condition. For the
free particle limit and the harmonic oscillator, where the Gaussian is
the exact solution, it obviously does but in general it does not.
as the initial point for the
imaginary time dynamics, it is not clear that the approximation given
in Eq. 3.27 automatically satisfies this condition. For the
free particle limit and the harmonic oscillator, where the Gaussian is
the exact solution, it obviously does but in general it does not.
As a specific example, we consider again the ground state limit of the
hydrogen atom in the Gaussian approximation. Using the ground state
values for the variational parameters, 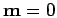 and
and 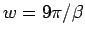 ,
Eq. 3.27 becomes,
,
Eq. 3.27 becomes,
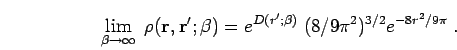 |
(165) |
For this to be symmetric under
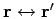 , we must have
, we must have
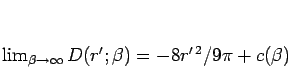 |
(166) |
and from the result for  ,
,
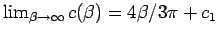 .
.
Figure 3.2 compares the 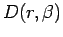 from the Gaussian VDM with
Eq. 3.48 using
from the Gaussian VDM with
Eq. 3.48 using
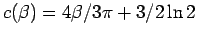 .
.
Figure 3.2:
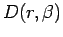 from the Gaussian approximation in the ground state limit
(solid line) of the hydrogen atom. Deviations of this function from linearity
indicate a breakdown of symmetry in the Gaussian approximation for
from the Gaussian approximation in the ground state limit
(solid line) of the hydrogen atom. Deviations of this function from linearity
indicate a breakdown of symmetry in the Gaussian approximation for
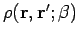 . The dashed line is
. The dashed line is
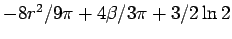 expected from the Rayleigh-Ritz
ground state Eq. 3.37.
expected from the Rayleigh-Ritz
ground state Eq. 3.37.
|
|
There are several consequences of this small violation of
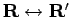 symmetry. As shown generally in the section
above, in the
symmetry. As shown generally in the section
above, in the
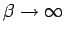 limit
limit 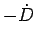 is the Rayleigh-Ritz
variational ground state energy for a Gaussian wave function, which
for the hydrogen atom is
is the Rayleigh-Ritz
variational ground state energy for a Gaussian wave function, which
for the hydrogen atom is
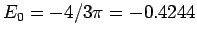 . Because of the loss
of symmetry this is not the same as the energy given by the estimator
. Because of the loss
of symmetry this is not the same as the energy given by the estimator
![\begin{displaymath}
\left<E\right> = \left<{\mathcal{H}}\right> \equiv \frac{\mbox{Tr}[{\mathcal{H}}\rho]}{\mbox{Tr}[\rho]}
\end{displaymath}](img667.png) |
(167) |
in the
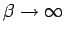 limit, which for the hydrogen atom gives the
more accurate result
limit, which for the hydrogen atom gives the
more accurate result
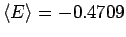 . This will be seen
again below for the hydrogen molecule where Eq. 3.49 also
gives more accurate ground state energies. Other consequences are
less pleasant. Although the energy is more accurate the virial
theorem,
. This will be seen
again below for the hydrogen molecule where Eq. 3.49 also
gives more accurate ground state energies. Other consequences are
less pleasant. Although the energy is more accurate the virial
theorem,
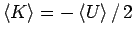 , between the kinetic and
potential energy is violated by about
, between the kinetic and
potential energy is violated by about 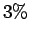 (while both are more
accurate than the usual ground state variational Gaussian
result). This has consequences for calculating the equation of state
particularly at low density. Slightly more complicated, explicitly
symmetric forms for the VDM could be used but in this paper we will
continue to explore the basic Gaussian approximation.
(while both are more
accurate than the usual ground state variational Gaussian
result). This has consequences for calculating the equation of state
particularly at low density. Slightly more complicated, explicitly
symmetric forms for the VDM could be used but in this paper we will
continue to explore the basic Gaussian approximation.




Next: Thermodynamic Estimators
Up: Variational Density Matrix Properties
Previous: Zero Temperature Limit
Contents
Burkhard Militzer
2003-01-15
![]() .
Since we have singled out
.
Since we have singled out ![]() as the initial point for the
imaginary time dynamics, it is not clear that the approximation given
in Eq. 3.27 automatically satisfies this condition. For the
free particle limit and the harmonic oscillator, where the Gaussian is
the exact solution, it obviously does but in general it does not.
as the initial point for the
imaginary time dynamics, it is not clear that the approximation given
in Eq. 3.27 automatically satisfies this condition. For the
free particle limit and the harmonic oscillator, where the Gaussian is
the exact solution, it obviously does but in general it does not.
![]() and
and ![]() ,
Eq. 3.27 becomes,
,
Eq. 3.27 becomes,
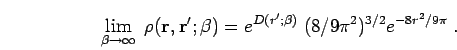
![]() from the Gaussian VDM with
Eq. 3.48 using
from the Gaussian VDM with
Eq. 3.48 using
![]() .
.
![\includegraphics[width=10cm]{figures3/Dvsr_hatom.eps}](img663.png)
![]() symmetry. As shown generally in the section
above, in the
symmetry. As shown generally in the section
above, in the
![]() limit
limit ![]() is the Rayleigh-Ritz
variational ground state energy for a Gaussian wave function, which
for the hydrogen atom is
is the Rayleigh-Ritz
variational ground state energy for a Gaussian wave function, which
for the hydrogen atom is
![]() . Because of the loss
of symmetry this is not the same as the energy given by the estimator
. Because of the loss
of symmetry this is not the same as the energy given by the estimator