Since the VDM, except in the simplest cases, is not exact various
estimators for the same quantity will differ. For example the
variational principle introduced in section II consists essentially in
globally minimizing the squared difference between
![]() and
and
![]() , either of which can be
used in estimating the energy. As mentioned above the energy estimator
Eq. 3.49 and its kinetic and potential energy pieces do
not automatically satisfy the virial theorem for Coulomb systems at
low density. As an alternative to Eq. 3.49, one can use
the thermodynamic estimators,
, either of which can be
used in estimating the energy. As mentioned above the energy estimator
Eq. 3.49 and its kinetic and potential energy pieces do
not automatically satisfy the virial theorem for Coulomb systems at
low density. As an alternative to Eq. 3.49, one can use
the thermodynamic estimators,
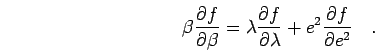 |
(172) |
In the zero temperature limit, the thermodynamic estimators satisfy
the virial theorem, which is also satisfied by any exact and any
variational Rayleigh-Ritz ground state. From the zero temperature
limit of the VDM given by Eq. 3.46 and the ![]() factor
in Eqs. 3.51 and 3.52, it is seen that the symmetry
error
factor
in Eqs. 3.51 and 3.52, it is seen that the symmetry
error
![]() is unimportant in this limit. It should be noted
that calculating the derivatives for
is unimportant in this limit. It should be noted
that calculating the derivatives for
![]() and
and
![]() increases the numerical work.
The pressure is estimated from
increases the numerical work.
The pressure is estimated from