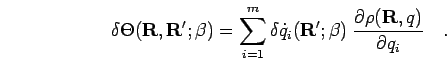Next: Analogy to Real-Time Wave
Up: Variational Density Matrix Technique
Previous: Analogy to Zero Temperature
Contents
Variational Principle for the Many Body Density Matrix
The Gibbs-Delbruck variational principle for the
free energy based on a trial density matrix
![\begin{displaymath}
F\leq \mbox{Tr}[\tilde{\rho}{\mathcal{H}}]+kT\;\mbox{Tr}[\tilde{\rho}\ln\tilde{\rho}]
\end{displaymath}](img558.png) |
(121) |
where
![\begin{displaymath}
\tilde{\rho}=\rho/\mbox{Tr}[\rho]
\end{displaymath}](img559.png) |
(122) |
is well known and convenient for discrete systems (e.g. Hubbard
models) but the logarithmic entropy term makes it difficult to apply
to continuous systems. Here, we propose a simpler variational
principle patterned after the Dirac-Frenkel-McLachlan variational
principle used in the time dependent quantum problem
(McLachlan, 1964). Consider the quantity
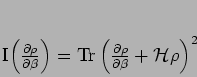 |
(123) |
as a functional of
 |
(124) |
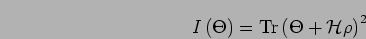 |
(125) |
with 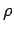 fixed.
fixed.
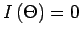 when
when 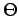 satisfies the Bloch equation,
satisfies the Bloch equation,
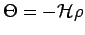 ,
and is otherwise positive. Varying
,
and is otherwise positive. Varying 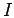 with
with 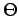 gives the minimum condition
gives the minimum condition
![\begin{displaymath}
\mbox{Tr}\;\left[ \delta\Theta\left(\Theta +{\mathcal{H}}\rho\right)\right]=0 \quad.
\end{displaymath}](img567.png) |
(126) |
This may be written in a real space basis as
![\begin{displaymath}
\int\int \delta\Theta({\bf R'},{\bf R};\beta)
\left[\Theta({...
...\bf R},{\bf R'};\beta)
\right] {\bf d}{\bf R}{\bf d}{\bf R'}=0
\end{displaymath}](img568.png) |
(127) |
or, using the symmetry of the density matrix in 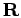 and
and 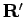 ,
,
![\begin{displaymath}
\int\int \delta\Theta({\bf R},{\bf R'};\beta)
\left[\Theta({...
...{\bf R'};\beta)
\right] {\bf d}{\bf R}{\bf d}{\bf R'}=0 \quad.
\end{displaymath}](img570.png) |
(128) |
Finally, we may consider a variation at some arbitrary, fixed 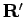 to get
to get
![\begin{displaymath}
\int \delta\Theta({\bf R},{\bf R'};\beta)
\left[\Theta({\bf ...
...{\bf R'};\beta)
\right] {\bf d}{\bf R}=0\;\;\forall {\bf R'}.
\end{displaymath}](img571.png) |
(129) |
It should be noted that in going from Eq. 3.9 to
Eq. 3.10 a density matrix symmetric
in 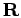 and
and 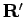 is assumed, which is a property of the exact
density matrix.
If the variational ansatz does not manifestly have this invariance
Eq. 3.11 minimizes the quantity,
is assumed, which is a property of the exact
density matrix.
If the variational ansatz does not manifestly have this invariance
Eq. 3.11 minimizes the quantity,
![\begin{displaymath}
\int
\left[\Theta({\bf R},{\bf R'};\beta)+{\mathcal{H}}\rho({\bf R},{\bf R'};\beta)
\right]^{2} {\bf d}{\bf R}=0 \quad.
\end{displaymath}](img572.png) |
(130) |
This represents the actual variational principle that will be used
throughout this work. By construction, it leads to an approximate
solution of the Bloch equation, which we propose to derive by
parameterizing the density matrix with a set of parameters 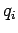 depending on imaginary time
depending on imaginary time 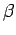 and
and 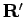 ,
,
 |
(131) |
so
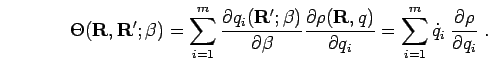 |
(132) |
In the imaginary time derivative
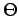 , only variations in
, only variations in 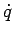 and not
and not 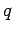 are considered since
are considered since
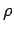 is fixed so,
is fixed so,
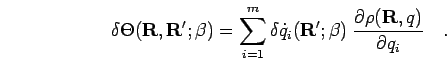 |
(133) |
Using this in equation 3.11 gives for each
variational parameter, since these are independent,
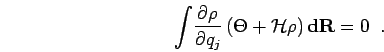 |
(134) |
This is the imaginary-time equivalent to the approach of Singer and Smith (1986)
for an approximate solution of the time dependent Schödinger equation using wave packets
(see section 3.3). Introducing the notation
 |
(135) |
and using Eq. 3.14,
the fundamental set of first order differential equations
for the dynamics of the variation parameters in imaginary time
follows from Eq.. 3.16 as,
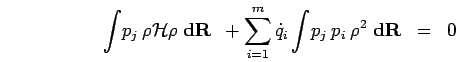 |
(136) |
or in matrix form
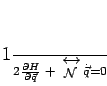 |
(137) |
where
 |
(138) |
and the norm matrix
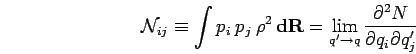 |
(139) |
with
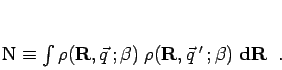 |
(140) |
The initial conditions follow from the free particle limit of the
density matrix at high temperature, 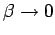 ,
,
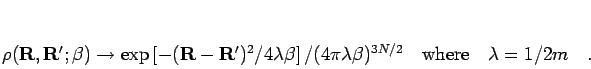 |
(141) |
Various ansatz forms for 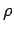 may now be used with this approach.
After considering the analogy to real time wave packet molecular dynamics, the
principle is first applied to the problem of a particle in an external field.
may now be used with this approach.
After considering the analogy to real time wave packet molecular dynamics, the
principle is first applied to the problem of a particle in an external field.




Next: Analogy to Real-Time Wave
Up: Variational Density Matrix Technique
Previous: Analogy to Zero Temperature
Contents
Burkhard Militzer
2003-01-15

![\begin{displaymath}
\int
\left[\Theta({\bf R},{\bf R'};\beta)+{\mathcal{H}}\rho({\bf R},{\bf R'};\beta)
\right]^{2} {\bf d}{\bf R}=0 \quad.
\end{displaymath}](img572.png)