Considerable effort has been devoted to systems where finite
temperature ions (treated either classically or quantum mechanically
by path integral methods) are coupled to degenerate electrons on the
Born-Oppenheimer surface. In contrast, the theory for similar systems
with non-degenerate electrons (![]() a significant fraction of
a significant fraction of ![]() )
is relatively underdeveloped except at the extreme high
)
is relatively underdeveloped except at the extreme high ![]() limit
where Thomas-Fermi and similar theories apply. In this chapter, we
present a variational approach for systems with non-degenerate
electrons analogous to the methods used for ground state many body
computations.
limit
where Thomas-Fermi and similar theories apply. In this chapter, we
present a variational approach for systems with non-degenerate
electrons analogous to the methods used for ground state many body
computations.
Although an oversimplification, we may usefully view the ground state computations as consisting of three levels of increasing accuracy (Hammond et al., 1994).
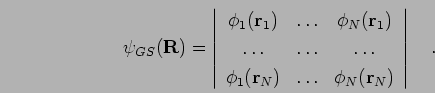 |
(119) |
The finite temperature theory proceeds similarly. Rather than the ground state wave function a thermal density matrix Eq. 2.5 is needed to compute the thermal averages of operators as shown in Eq. 2.7.
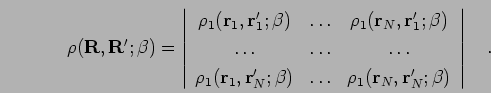 |
(120) |
![[*]](crossref.png) .
This method has been extensively applied using the free particle nodes
(Magro et al., 1996; Pierleoni et al., 1994). One aim of the approach is to provide more
realistic nodal structures as input to PIMC.
.
This method has been extensively applied using the free particle nodes
(Magro et al., 1996; Pierleoni et al., 1994). One aim of the approach is to provide more
realistic nodal structures as input to PIMC.
This chapter considers the first level in this approach. The next
section is devoted to a general variational principle which will be
used to determine the many body density matrix. The principle is then
applied to the problem of a single particle in an external potential
and compared to exact results for the hydrogen atom density
matrix. After a discussion of some general properties, many body
applications are considered starting with a hydrogen molecule and then
proceeding to warm, dense hydrogen. It is shown that the method and
the ansatz considered can describe dense hydrogen in the molecular,
the dissociated and the plasma regime. Structural and thermodynamic
properties for this system over a range of temperatures (T![]() to
to
![]() ) and densities (electron sphere radius
) and densities (electron sphere radius ![]() to
to
![]() ) are presented.
) are presented.