Wave packet molecular dynamics (WPMD) was first used by Heller (1975) and later
applied to scattering processes in nuclear physics (Feldmeier, 1990)
and plasma physics (Klakow et al., 1994b; Ebeling and Militzer, 1997).
An ansatz for the wave function ![]() is made and the
equation of motions
for the parameters
is made and the
equation of motions
for the parameters ![]() in real time can be derived from the
principle of stationary action (Feldmeier, 1990),
in real time can be derived from the
principle of stationary action (Feldmeier, 1990),
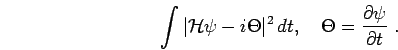 |
(143) |
The VDM approach and WPMD method share the zero temperate limit, which is given by the Rayleigh-Ritz principle (see section 3.5.1). At high temperature, the width of wave packets in WPMD grows without limits, which is a known problem of this method (Knaup et al., 1999; Militzer, 1996). In the VDM approach, the correct high temperature limit of free particles is included. The average width shown in Fig. 3.11 can be used to verify the attempts to correct the dynamics of the real time wave packets by Knaup et al. (1999).