



Next: Loss of Symmetry
Up: Variational Density Matrix Properties
Previous: Variational Density Matrix Properties
Contents
Zero Temperature Limit
In the preceding section, it was shown that for the hydrogen atom the
Gaussian variational density matrix, as a function of 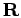 converges
at low temperature to the Gaussian ground state wave function given by
the Rayleigh-Ritz variational principle. It is generally true that the
Rayleigh-Ritz ground state
corresponds to the zero temperature limit of the VDM as we now show.
converges
at low temperature to the Gaussian ground state wave function given by
the Rayleigh-Ritz variational principle. It is generally true that the
Rayleigh-Ritz ground state
corresponds to the zero temperature limit of the VDM as we now show.
The Rayleigh-Ritz principle states that for any real parameterized
wave function
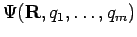 the variational energy
the variational energy
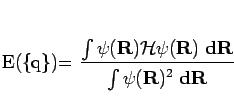 |
(156) |
is greater than or equal to the true ground state energy even at the minimum determined
by
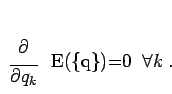 |
(157) |
For the VDM ansatz, an amplitude parameter 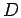 is assumed such that
is assumed such that
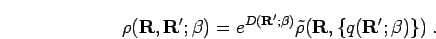 |
(158) |
As in the one particle example, it is expected that at low
temperature,
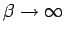 , the other
, the other
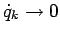 while
while
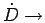 constant. From this assumption, Eq. 3.19 implies
that as
constant. From this assumption, Eq. 3.19 implies
that as
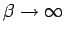
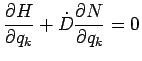 |
|
|
(159) |
for all variational parameters, where we have defined
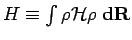 and
and
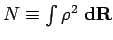 . Since
. Since
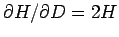 and
and
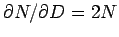 ,
Eq. 3.41 for
,
Eq. 3.41 for
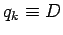 implies
implies
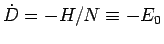 . So Eq. 3.41 may be rewritten as
. So Eq. 3.41 may be rewritten as
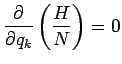 |
|
|
(160) |
at the
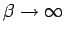 fixed point. With the correspondence
fixed point. With the correspondence
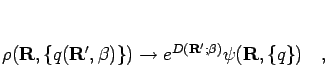 |
(161) |
this is equivalent to Eq. 3.39 and thus the Rayleigh-Ritz ground
state corresponds to a zero temperature fixed point in the dynamics of
the parameters.
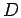 is a function of
is a function of 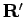 and
and 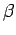 , which is calculated by
integrating from
, which is calculated by
integrating from 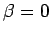 with Eq. 3.23 as initial conditions.
The zero temperature limit of
with Eq. 3.23 as initial conditions.
The zero temperature limit of 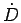 is a constant,
is a constant, 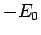 , which
means in the low temperature limit
, which
means in the low temperature limit 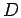 can written as
can written as
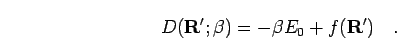 |
(162) |
The function 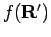 can be rewritten as,
can be rewritten as,
![\begin{displaymath}
f({\bf R'}) = \ln \left\{ \psi_0({\bf R'}) \left[ \, 1 + \delta({\bf R'}) \, \right] \right\}\quad,
\end{displaymath}](img653.png) |
(163) |
where the function
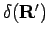 is introduced to describe the
variational error in the solution of the Bloch equation. It is
identical to zero if the variational ansatz includes the exact
solution. It leads to loss of symmetry in
is introduced to describe the
variational error in the solution of the Bloch equation. It is
identical to zero if the variational ansatz includes the exact
solution. It leads to loss of symmetry in 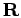 and
and 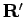 , which will
discussed in the next section. Eq. 3.43 now reads,
, which will
discussed in the next section. Eq. 3.43 now reads,
![\begin{displaymath}
\rho({\bf R},{\bf R'},\beta\to\infty) = e^{-\beta E_0} \ps...
...}) \psi_0({\bf R'})
\left[ 1 + \delta({\bf R'}) \right]
\quad.
\end{displaymath}](img655.png) |
(164) |
For certain potentials, several fixed points of the dynamics can
exist. From Eq. 3.46, it follows that only the lowest energy
state contributes to physical observables calculated from
Eq. 2.4. This completes the argument that the zero
temperature limit of the VDM corresponds to the Rayleigh-Ritz ground
state.
In the case of an anti-symmetrized ansatz for the density matrix,
it can be shown that the fixed point of the dynamics in imaginary time
corresponds to the Rayleigh-Ritz ground state for an anti-symmetrized
wave function.




Next: Loss of Symmetry
Up: Variational Density Matrix Properties
Previous: Variational Density Matrix Properties
Contents
Burkhard Militzer
2003-01-15
![]() the variational energy
the variational energy
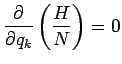
![]() is a function of
is a function of ![]() and
and ![]() , which is calculated by
integrating from
, which is calculated by
integrating from ![]() with Eq. 3.23 as initial conditions.
The zero temperature limit of
with Eq. 3.23 as initial conditions.
The zero temperature limit of ![]() is a constant,
is a constant, ![]() , which
means in the low temperature limit
, which
means in the low temperature limit ![]() can written as
can written as