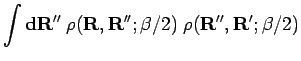 |
(192) | ||
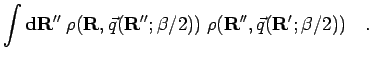 |
(193) |
Alternatively, one can try an approximation to the convolution in
Eq. 3.74,
Furthermore, the Gaussian ansatz can be improved by including
additional variational parameters, e.g. to use a sum of Gaussians. In
the zero temperature limit, this would lead to a solution closer to the
Hartree Fock result. To go beyond one needs to include additional
correlations in the ansatz and derive modified equations for the
parameter from Eq. 3.19. Correlations are usually introduced
with a Jastrow factor, which can be generalized to finite
temperature. The new ansatz then reads,
Alternatively, one can use an unitary correlation operator as suggested by Schnack (1996). The idea is to applied a short range correlation operator to an uncorrelated state in order to generate a correlated state. The fundamental difference to the Jastrow type ansatz above that correlations are introduced by the operator.
Another improvement for many-particle simulations would be to consider
all ![]() terms from the permutations, which would make contributions
at very high levels of degeneracy. The scaling of a full exchange
method can be reduced to
terms from the permutations, which would make contributions
at very high levels of degeneracy. The scaling of a full exchange
method can be reduced to ![]() as suggested by Schnack (1996) for real
time wave packet molecular dynamics but the application of this method
to the VDM imaginary time remains to be done.
as suggested by Schnack (1996) for real
time wave packet molecular dynamics but the application of this method
to the VDM imaginary time remains to be done.
To summarize, one can say that the VDM approach provides a way to systematically improve the many-particle density matrix. Already the simplest ansatz using one Gaussian to describe the single particle density matrices gives a good description of hydrogen in the discussed range of temperature and density. The method includes the correct high temperature behavior and shows the expected formation of atoms and molecules. The thermodynamic variables are in reasonable agreement with PIMC simulations and lead to a good approximation of the Hugoniot function. Further one can use this essentially analytic density matrix to furnish the nodal surface in PIMC simulations, replacing the free particle nodes by a density matrix that already includes the principle physical effects. Results will be discussed in the next chapter.