Next: Results from Many-Particle Simulations
Up: Variational Density Matrix Technique
Previous: Variational Many-Particle Density Matrix
Contents
Antisymmetry in the Parameter Equations
The determinantal form for the VDM, Eq. 3.56, is correctly
antisymmetric under exchange of identical particles. Since ion
exchange effects are negligible at the temperatures considered here
these are ignored.
The determinantal form leads to 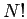 terms in the equations of motion
for the variational parameters presented in appendix A. It was
originally hoped that exchange effects could be ignored in these
equations while retaining the full determinantal form for the VDM but
this leads to an instability in fermionic systems, e.g. it results in
an unphysical strong attraction between two hydrogen molecules.
terms in the equations of motion
for the variational parameters presented in appendix A. It was
originally hoped that exchange effects could be ignored in these
equations while retaining the full determinantal form for the VDM but
this leads to an instability in fermionic systems, e.g. it results in
an unphysical strong attraction between two hydrogen molecules.
A practical means of treating all exchange terms, in particular terms
involving the potential energy, in the variational parameter equations
was not found. Instead it was necessary to use an approximation
similar to that used in the real time computations
(Knaup et al., 1999; Klakow et al., 1994b): only pair exchanges in the kinetic energy terms
were retained. This will be illustrated for the hydrogen molecule
after first giving the explicit form for this correction. It is
stressed that, unlike the real time computations, once the variational
parameters are determined the full determinantal form is then used in
calculating the various averages.
For two particles with parallel spin, the correction term to the kinetic energy
is given by,
For the Gaussian ansatz in Eq. 3.56 it becomes,
The corrections to the norm matrix 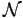 are neglected in order to keep its analytically
invertible form.
The corrections to
are neglected in order to keep its analytically
invertible form.
The corrections to 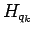 in Eq. 3.62 are given by
in Eq. 3.62 are given by
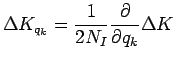 |
|
|
(187) |
The correction to dynamics of the parameters follow from Eq. 3.59 to 3.61,
These equations lead to an effective repulsion between the Gaussians
for two electrons with parallel spin if there is significant overlap.
As a example of this effect the variational parameters for the singlet
and triplet states of the hydrogen molecule are compared in
Fig. 3.4. For the triplet state parameters, the solution
including full exchange effects (long dashed line) are compared with
those obtained in the kinetic pair exchange approximation (dot-dashed
line). The approximation now prevents the Gaussian means for the same
spin electrons from collapsing to the bond center at lower temperature
and is numerically close to the solution for full exchange.
Figure 3.4:
Effect of antisymmetry on the density matrix parameters, width and mean, for a
hydrogen molecule. The protons (large black dots along x
axis) are separated by 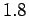 and the initial electron
positions
and the initial electron
positions
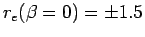 along the molecular
axis. The solid line for the singlet state (electron spins
anti-parallel) shows both electrons centered in the
molecular bond at low temperatures (large
along the molecular
axis. The solid line for the singlet state (electron spins
anti-parallel) shows both electrons centered in the
molecular bond at low temperatures (large 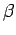 ). In the
triplet state (parallel electron spins), the electrons are
centered close to the protons (long dashed line). The
approximation that includes only kinetic exchanges
(dot-dashed line) gives a similar result for the mean, with
the electrons centered slightly inside the protons but
overestimates the Gaussian width (left panel). At high
temperature (
). In the
triplet state (parallel electron spins), the electrons are
centered close to the protons (long dashed line). The
approximation that includes only kinetic exchanges
(dot-dashed line) gives a similar result for the mean, with
the electrons centered slightly inside the protons but
overestimates the Gaussian width (left panel). At high
temperature (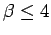 ), exchange is unimportant and the
parameters are nearly the same for all cases.
), exchange is unimportant and the
parameters are nearly the same for all cases.
|
|
Even at the lowest temperature considered here in the dense hydrogen
simulations (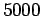 K) exchange effects between same spin electrons
are negligible beyond a few angstroms, i.e. one or perhaps two
nearest neighbors. Fig. 3.4 for the triplet state thus
overestimates the effect likely in dense hydrogen. The main effect of
including exchange in the parameter equations is probably to prevent
the instability mentioned above.
K) exchange effects between same spin electrons
are negligible beyond a few angstroms, i.e. one or perhaps two
nearest neighbors. Fig. 3.4 for the triplet state thus
overestimates the effect likely in dense hydrogen. The main effect of
including exchange in the parameter equations is probably to prevent
the instability mentioned above.
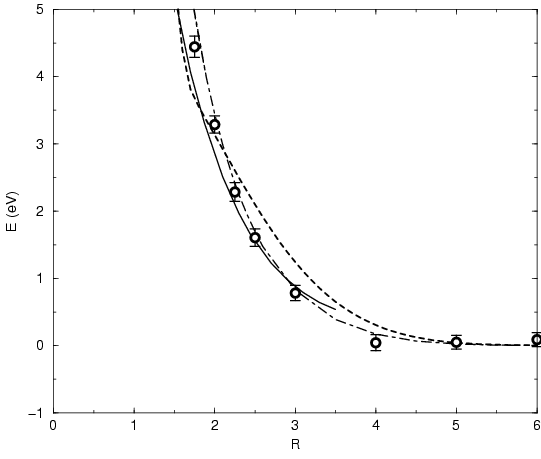
Fig. 3.5 shows an energy comparison for the triplet ground
state of the hydrogen molecule. First, we compare the Gaussian
approximation using only the kinetic exchange term in the parameter
equations. For the direct estimator, Eq. 3.49, one finds
fairly good agreement with the accurate quantum chemistry result
(Kolos and Roothan, 1969). The thermodynamic estimator gives a somewhat more
repulsive triplet interaction for 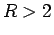 . Considering also the Coulomb
exchange terms in the Gaussian approximation leads to the dot-dashed
line for the thermodynamic estimator. We conclude that leaving out the
Coulomb exchange terms in the parameter equations for efficiency
reasons is a reasonable approximation in many-particle simulations.
. Considering also the Coulomb
exchange terms in the Gaussian approximation leads to the dot-dashed
line for the thermodynamic estimator. We conclude that leaving out the
Coulomb exchange terms in the parameter equations for efficiency
reasons is a reasonable approximation in many-particle simulations.
Figure 3.5:
Energy of repulsion for the triplet ground state of the
hydrogen molecule for bond length 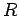 .
The thermodynamic (dashed line) and the direct estimator, Eq.
3.49, (circles with error bars) for the
Gaussian approximation using the kinetic exchange term
in the parameter equations
are compared with the Kolos and Roothan results (solid line).
The thermodynamic estimator
for the Gaussian approximation with all exchange terms is shown by the dot-dashed line.
.
The thermodynamic (dashed line) and the direct estimator, Eq.
3.49, (circles with error bars) for the
Gaussian approximation using the kinetic exchange term
in the parameter equations
are compared with the Kolos and Roothan results (solid line).
The thermodynamic estimator
for the Gaussian approximation with all exchange terms is shown by the dot-dashed line.
|
|




Next: Results from Many-Particle Simulations
Up: Variational Density Matrix Technique
Previous: Variational Many-Particle Density Matrix
Contents
Burkhard Militzer
2003-01-15
![]() terms in the equations of motion
for the variational parameters presented in appendix A. It was
originally hoped that exchange effects could be ignored in these
equations while retaining the full determinantal form for the VDM but
this leads to an instability in fermionic systems, e.g. it results in
an unphysical strong attraction between two hydrogen molecules.
terms in the equations of motion
for the variational parameters presented in appendix A. It was
originally hoped that exchange effects could be ignored in these
equations while retaining the full determinantal form for the VDM but
this leads to an instability in fermionic systems, e.g. it results in
an unphysical strong attraction between two hydrogen molecules.
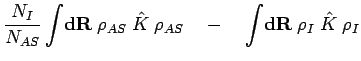
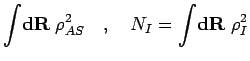
![$\displaystyle -
\frac{4 \lambda N_I }{w N_Q}
\left[ \, 3 \left(1-\tilde{w}^2\right)-Q^2 \right]
\quad,$](img716.png)
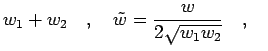
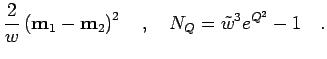
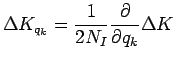
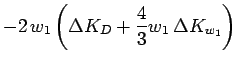
![\includegraphics[width=10cm]{figures3/antisym03.eps}](img729.png)
![]() . Considering also the Coulomb
exchange terms in the Gaussian approximation leads to the dot-dashed
line for the thermodynamic estimator. We conclude that leaving out the
Coulomb exchange terms in the parameter equations for efficiency
reasons is a reasonable approximation in many-particle simulations.
. Considering also the Coulomb
exchange terms in the Gaussian approximation leads to the dot-dashed
line for the thermodynamic estimator. We conclude that leaving out the
Coulomb exchange terms in the parameter equations for efficiency
reasons is a reasonable approximation in many-particle simulations.