|

|
|
|
|
|
The equation of state (EOS) is central interest in theoretical plasma physics since it is the basic thermodynamic quantity. It is also the key property to test the accuracy of different approaches to hot, dense hydrogen including analytical theories and numerical models. If the predicted EOS seems reasonable, one can have more confidence in all derived properties. The complete EOS data from our PIMC simulations can be found in tables in App. D.
First, we picked the density corresponding to ![]() and compared
pressure and energy as a function of temperature. We separated the
analysis in the high temperature behavior
and compared
pressure and energy as a function of temperature. We separated the
analysis in the high temperature behavior
![]() where
thermal excitations dominate, and the low temperature regime
where
thermal excitations dominate, and the low temperature regime
![]() where Coulomb effects and bound states are most relevant.
where Coulomb effects and bound states are most relevant.
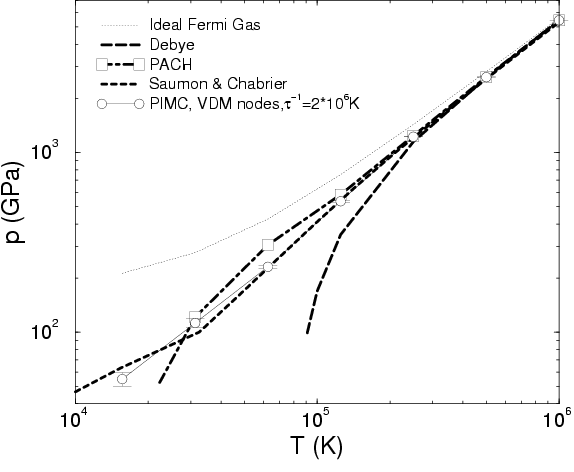
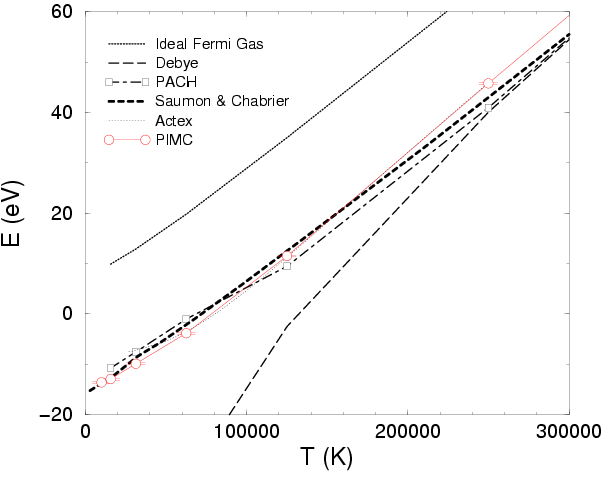
The pressure and energy in the high temperature regime are shown in
Figs. ![[*]](crossref.png) and
and ![[*]](crossref.png) . In the high temperature
limit, kinetic effects are dominant and the hydrogen plasma behaves
like a gas of non-interacting protons and electrons. The leading
corrections are given by Debye screening effects (see
App. C) that scale with the coupling parameter
. In the high temperature
limit, kinetic effects are dominant and the hydrogen plasma behaves
like a gas of non-interacting protons and electrons. The leading
corrections are given by Debye screening effects (see
App. C) that scale with the coupling parameter
![]() . For small values of
. For small values of ![]() , the (fully ionized)
Debye model is a reliable approximation. One finds deviations of less
than
, the (fully ionized)
Debye model is a reliable approximation. One finds deviations of less
than ![]() in pressure and energy for
in pressure and energy for ![]() at
at ![]() . For
higher values of
. For
higher values of ![]() , quantum effects such as the formation of
bound state at low density and degeneracy effects at high density
limit the validity. Various extensions to the Debye model have been
made, see (Ebeling et al., 1976). However, at sufficiently high
, quantum effects such as the formation of
bound state at low density and degeneracy effects at high density
limit the validity. Various extensions to the Debye model have been
made, see (Ebeling et al., 1976). However, at sufficiently high ![]() ,
the Debye model overestimates the screening drastically and leads to
unphysically low, even negative pressures.
,
the Debye model overestimates the screening drastically and leads to
unphysically low, even negative pressures.
Figs. ![[*]](crossref.png) and
and ![[*]](crossref.png) include a comparison
with EOS model by Saumon and Chabrier (1992), the Padé approximations in the
chemical picture (PACH) by Ebeling and Richert (1985a), and the activity expansion
(Actex) by Rogers (1990). The observed deviations are a result of how
interaction and degeneracy effects are treated in those models.
include a comparison
with EOS model by Saumon and Chabrier (1992), the Padé approximations in the
chemical picture (PACH) by Ebeling and Richert (1985a), and the activity expansion
(Actex) by Rogers (1990). The observed deviations are a result of how
interaction and degeneracy effects are treated in those models.
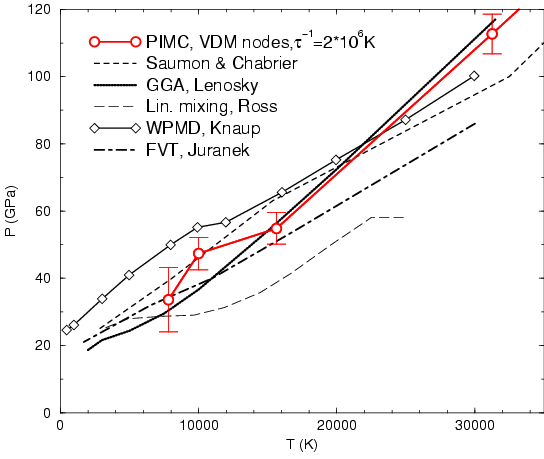
In Figs. ![[*]](crossref.png) and
and ![[*]](crossref.png) , we compare pressure
and energy in the low temperature regime. The EOS properties are
determined by a strong coupling combined with a high degeneracy
(
, we compare pressure
and energy in the low temperature regime. The EOS properties are
determined by a strong coupling combined with a high degeneracy
(
![]() ). The comparison includes EOS by
Saumon and Chabrier (1992), the DFT-MD by Lenosky et al. (2000), the fluid
variational theory by Juranek and Redmer (2000), the wave-packet MD by
Knaup et al. (2000), the linear mixing model by Ross (1998), and PIMC simulations
using free particle nodes and
). The comparison includes EOS by
Saumon and Chabrier (1992), the DFT-MD by Lenosky et al. (2000), the fluid
variational theory by Juranek and Redmer (2000), the wave-packet MD by
Knaup et al. (2000), the linear mixing model by Ross (1998), and PIMC simulations
using free particle nodes and
![]() . For this
density, we found the best agreement of our results with the work by
DFT-MD by Lenosky et al. (2000).
. For this
density, we found the best agreement of our results with the work by
DFT-MD by Lenosky et al. (2000).
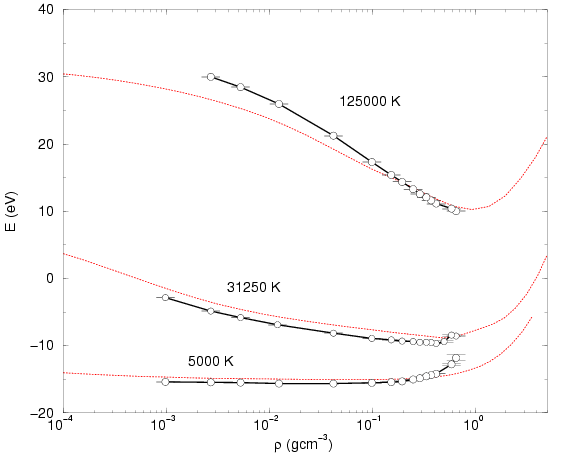
Finally, we present a comparison of internal energy and pressure as a
function of density for different
temperatures. Fig. ![[*]](crossref.png) shows a reasonably good
agreement in the energy between the EOS by Saumon and Chabrier (1992) and our
simulation results over a broad range of densities. PIMC energies for
low temperatures and densities are consistently lower by the order 1
or 2 eV per atom. For low density and high temperature, relatively
large deviations were observed, which is surprising because in this
regime, one expects both methods to work very well.
shows a reasonably good
agreement in the energy between the EOS by Saumon and Chabrier (1992) and our
simulation results over a broad range of densities. PIMC energies for
low temperatures and densities are consistently lower by the order 1
or 2 eV per atom. For low density and high temperature, relatively
large deviations were observed, which is surprising because in this
regime, one expects both methods to work very well.
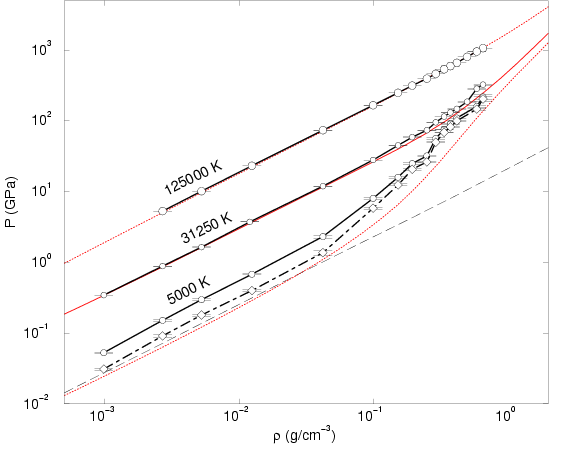
Studying the pressure as function of density in
Fig. ![[*]](crossref.png) , one finds remarkably good agreement for
, one finds remarkably good agreement for
![]() and
and
![]() . For 5000 K, the PIMC pressure is
far too high because hydrogen under these conditions is a weakly
interacting molecular gas with possibly a very small degree of
dissociation caused by entropy effects. The PIMC pressure is about
twice the expected value, which is a result of the inaccuracies in the
pair density matrices discussed in
section
. For 5000 K, the PIMC pressure is
far too high because hydrogen under these conditions is a weakly
interacting molecular gas with possibly a very small degree of
dissociation caused by entropy effects. The PIMC pressure is about
twice the expected value, which is a result of the inaccuracies in the
pair density matrices discussed in
section ![[*]](crossref.png) . After those
corrections have been applied one finds better but not perfect
agreement. New calculations with improved density matrices remain to
be done.
. After those
corrections have been applied one finds better but not perfect
agreement. New calculations with improved density matrices remain to
be done.