



Next: Equation of State
Up: Thermodynamic Properties of Dense
Previous: Comparison of Variational and
Contents
Pair Correlation Functions
In this section, we compare the pair correlation functions for
different densities and temperatures from PIMC simulations using free
particle and VDM nodes. The pair correlation function is defined as
(Allen and Tildesley, 1987),
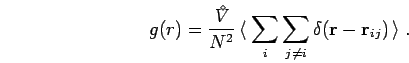 |
(202) |
Figure:
Proton-proton pair correlation functions multiplied by the density 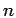 from PIMC
simulations of hydrogen using free particle nodes. The
columns correspond to different
from PIMC
simulations of hydrogen using free particle nodes. The
columns correspond to different 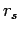 values and the rows to
different temperatures
values and the rows to
different temperatures 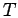 .
.
|
|
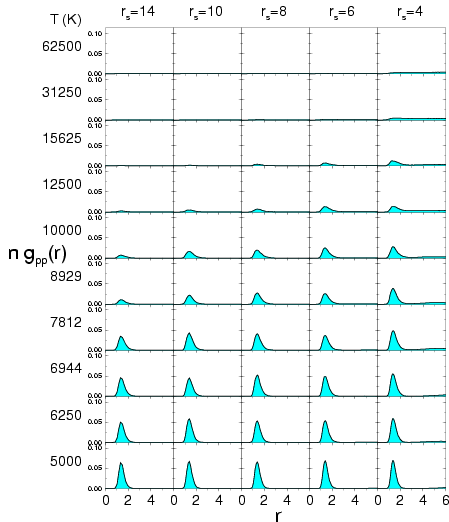
Figure:
Proton-proton pair correlation functions multiplied by the density 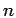 as in Fig.
as in Fig. ![[*]](crossref.png) but for deuterium at higher
densities.
but for deuterium at higher
densities.
|
|
It goes to 1 in the limit of large 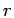 in an infinite system and to
in an infinite system and to
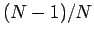 in a system of
in a system of 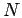 particles. The proton-proton pair
correlation functions from PIMC simulations with free particle nodes
are shown in Figs.
particles. The proton-proton pair
correlation functions from PIMC simulations with free particle nodes
are shown in Figs. ![[*]](crossref.png) and
and
![[*]](crossref.png) . For
. For
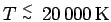 a peak at the bond length of
a peak at the bond length of 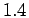 emerge,
which clearly demonstrates the formation of molecules. In the low
density region, we find it useful to multiply the pair correlation
function by an extra density factor
emerge,
which clearly demonstrates the formation of molecules. In the low
density region, we find it useful to multiply the pair correlation
function by an extra density factor
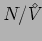 so that the area under
the peak is proportional to the molecular fraction. For
so that the area under
the peak is proportional to the molecular fraction. For
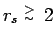 ,
the peak height gets smaller with decreasing density as a result of
entropy dissociation. Thermal dissociation reduces the number of
molecules with increasing temperature. For
,
the peak height gets smaller with decreasing density as a result of
entropy dissociation. Thermal dissociation reduces the number of
molecules with increasing temperature. For
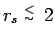 , pressure
dissociation diminishes the peak with increasing density. For PIMC
with free particle nodes, this process occurs within a small density
interval, in which the system undergoes a transition from a molecular
to a metallic regime (see Fig.
, pressure
dissociation diminishes the peak with increasing density. For PIMC
with free particle nodes, this process occurs within a small density
interval, in which the system undergoes a transition from a molecular
to a metallic regime (see Fig. ![[*]](crossref.png) ).
).
Figure:
Proton-proton pair correlation function from PIMC
simulations of deuterium using VDM nodes. The
columns correspond to different 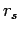 values and the rows to
different temperatures
values and the rows to
different temperatures 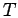 .
.
|
|
Figure:
Proton-proton pair correlation function as in Fig. ![[*]](crossref.png) but for higher densities.
but for higher densities.
|
|
Fig. ![[*]](crossref.png) and
and ![[*]](crossref.png) show the
proton-proton pair correlation functions from PIMC simulations with VDM
nodes using the standard normalization from Eq.
show the
proton-proton pair correlation functions from PIMC simulations with VDM
nodes using the standard normalization from Eq. ![[*]](crossref.png) . We also
included simulations at higher densities corresponding to
. We also
included simulations at higher densities corresponding to 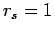 . The
molecular peak disappears gradually with increasing density,
indicating that pressure dissociation leads to a smooth transition to a
metallic regime.
. The
molecular peak disappears gradually with increasing density,
indicating that pressure dissociation leads to a smooth transition to a
metallic regime.
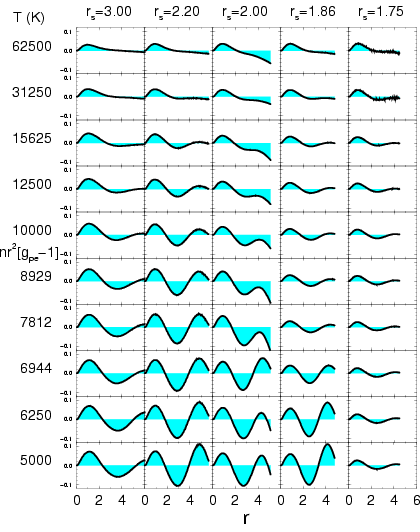
Figure:
Proton-electron radial correlation
function multiplied by the density,
![$n\,r^2\,[g_{pe}(r)-1]$](img889.png) from PIMC with free particle nodes. The columns correspond to
different
from PIMC with free particle nodes. The columns correspond to
different 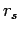 values and the rows to different temperatures
values and the rows to different temperatures
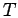 .
.
|
|
Figure:
Proton-electron pair correlation function from PIMC
simulations of deuterium using VDM nodes. The
columns correspond to different 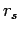 values and the rows to
various temperatures.
values and the rows to
various temperatures.
|
|
Figure:
Proton-electron pair correlation function as in Fig. ![[*]](crossref.png) but for higher densities.
but for higher densities.
|
|
Figure:
Electron-electron pair correlation function from PIMC
simulations of deuterium using VDM nodes. Solid lines
correspond to pairs with parallel spins and dashed lines to
anti-parallel spins. The columns belong to different 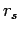 values and the rows to various temperatures
values and the rows to various temperatures 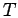 .
.
|
|
Figure:
Electron-electron pair correlation function as in Fig. ![[*]](crossref.png) but for higher densities.
but for higher densities.
|
|
The proton-electron radial distribution function
![$r^2[g_{pe}(r)-1]$](img894.png) from different simulations using free particle nodes is shown in
Fig.
from different simulations using free particle nodes is shown in
Fig. ![[*]](crossref.png) . For non-interacting particles, this function
would be identical to zero. The first peak shows an increased
probability of finding a electron near a proton due to the attractive
forces. At low temperature, the size of peak can also be interpreted
as the occupation of bound electronic states. Also the unbound,
scattering states lead to a smaller but non-zero contribution to this
peak. However, one can still deduce that the degree of ionization,
inversely related to the peak size, increases with temperature.
. For non-interacting particles, this function
would be identical to zero. The first peak shows an increased
probability of finding a electron near a proton due to the attractive
forces. At low temperature, the size of peak can also be interpreted
as the occupation of bound electronic states. Also the unbound,
scattering states lead to a smaller but non-zero contribution to this
peak. However, one can still deduce that the degree of ionization,
inversely related to the peak size, increases with temperature.
Alternatively, one can study the proton-electron pair correlation function
as shown in Fig. ![[*]](crossref.png) and
and
![[*]](crossref.png) from simulations using VDM nodes, where the
same overall behavior is represented in a different form.
Fig.
from simulations using VDM nodes, where the
same overall behavior is represented in a different form.
Fig. ![[*]](crossref.png) and
and ![[*]](crossref.png) show the
electron-electron pair-correlation functions. The peak for pairs with
anti-parallel electron spins indicates the formation of molecules, in
which two electrons get very close, in cases where they realize the
molecular binding. For same spin electrons, one always finds a strong
repulsion due to the Pauli exclusion principle.
show the
electron-electron pair-correlation functions. The peak for pairs with
anti-parallel electron spins indicates the formation of molecules, in
which two electrons get very close, in cases where they realize the
molecular binding. For same spin electrons, one always finds a strong
repulsion due to the Pauli exclusion principle.




Next: Equation of State
Up: Thermodynamic Properties of Dense
Previous: Comparison of Variational and
Contents
Burkhard Militzer
2003-01-15
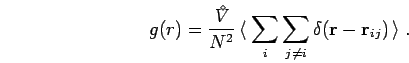
![[*]](crossref.png) and
and
![[*]](crossref.png) . For
. For
![[*]](crossref.png) ).
).
![\includegraphics[angle=0,width=14cm]{figures4/gpp05.eps}](img885.png)
![[*]](crossref.png) and
and ![[*]](crossref.png) show the
proton-proton pair correlation functions from PIMC simulations with VDM
nodes using the standard normalization from Eq.
show the
proton-proton pair correlation functions from PIMC simulations with VDM
nodes using the standard normalization from Eq. ![[*]](crossref.png) . We also
included simulations at higher densities corresponding to
. We also
included simulations at higher densities corresponding to ![]() . The
molecular peak disappears gradually with increasing density,
indicating that pressure dissociation leads to a smooth transition to a
metallic regime.
. The
molecular peak disappears gradually with increasing density,
indicating that pressure dissociation leads to a smooth transition to a
metallic regime.
![\includegraphics[angle=0,width=14cm]{figures4/gpe03.eps}](img890.png)
![\includegraphics[angle=0,width=14cm]{figures4/gee01.eps}](img892.png)
![]() from different simulations using free particle nodes is shown in
Fig.
from different simulations using free particle nodes is shown in
Fig. ![[*]](crossref.png) . For non-interacting particles, this function
would be identical to zero. The first peak shows an increased
probability of finding a electron near a proton due to the attractive
forces. At low temperature, the size of peak can also be interpreted
as the occupation of bound electronic states. Also the unbound,
scattering states lead to a smaller but non-zero contribution to this
peak. However, one can still deduce that the degree of ionization,
inversely related to the peak size, increases with temperature.
. For non-interacting particles, this function
would be identical to zero. The first peak shows an increased
probability of finding a electron near a proton due to the attractive
forces. At low temperature, the size of peak can also be interpreted
as the occupation of bound electronic states. Also the unbound,
scattering states lead to a smaller but non-zero contribution to this
peak. However, one can still deduce that the degree of ionization,
inversely related to the peak size, increases with temperature.
![[*]](crossref.png) and
and
![[*]](crossref.png) from simulations using VDM nodes, where the
same overall behavior is represented in a different form.
Fig.
from simulations using VDM nodes, where the
same overall behavior is represented in a different form.
Fig. ![[*]](crossref.png) and
and ![[*]](crossref.png) show the
electron-electron pair-correlation functions. The peak for pairs with
anti-parallel electron spins indicates the formation of molecules, in
which two electrons get very close, in cases where they realize the
molecular binding. For same spin electrons, one always finds a strong
repulsion due to the Pauli exclusion principle.
show the
electron-electron pair-correlation functions. The peak for pairs with
anti-parallel electron spins indicates the formation of molecules, in
which two electrons get very close, in cases where they realize the
molecular binding. For same spin electrons, one always finds a strong
repulsion due to the Pauli exclusion principle.