![[*]](crossref.png) and in the
histogram of the permutation probabilities in
Fig.
and in the
histogram of the permutation probabilities in
Fig. ![[*]](crossref.png) . For this reason, we focus in the discussion on
the two densities corresponding to
. For this reason, we focus in the discussion on
the two densities corresponding to
In this section, we are going to compare thermodynamic properties
derived from PIMC simulations of deuterium with free particle nodes
with those using VDM nodes. The effect of the nodal surfaces is
largest in the region of a high degree of electronic degeneracy, found
at high density and low temperature. It should be noted for low
densities e.g. ![]() , electrons become bound and localized
before a significant degree of degeneracy is reached. This can be seen
in the phase diagram in Fig.
, electrons become bound and localized
before a significant degree of degeneracy is reached. This can be seen
in the phase diagram in Fig. ![[*]](crossref.png) and in the
histogram of the permutation probabilities in
Fig.
and in the
histogram of the permutation probabilities in
Fig. ![[*]](crossref.png) . For this reason, we focus in the discussion on
the two densities corresponding to
. For this reason, we focus in the discussion on
the two densities corresponding to ![]() and
and ![]() where the
electronic degeneracy becomes very important for
where the
electronic degeneracy becomes very important for
![]() .
.
|
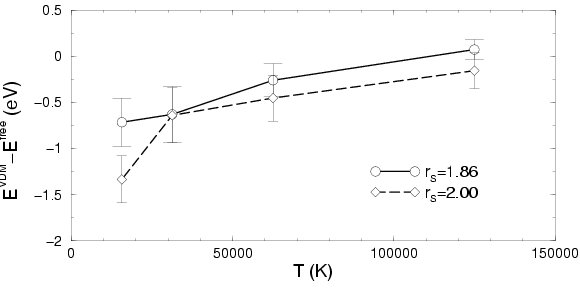
In Fig. ![[*]](crossref.png) , a comparison of the internal energy from
simulations with FP and VDM nodes is shown. Simulations with VDM nodes
lead to lower internal energies than those with FP nodes. The
differences become smaller with increasing temperature since the both
density matrices are exact in this limit. Since the free energy
, a comparison of the internal energy from
simulations with FP and VDM nodes is shown. Simulations with VDM nodes
lead to lower internal energies than those with FP nodes. The
differences become smaller with increasing temperature since the both
density matrices are exact in this limit. Since the free energy ![]() is
the integral of the internal energy over temperature, one can conclude
that VDM nodes yield to a smaller
is
the integral of the internal energy over temperature, one can conclude
that VDM nodes yield to a smaller ![]() and hence, are the more
appropriate nodal surface.
and hence, are the more
appropriate nodal surface.
![\includegraphics[angle=0,width=13cm]{figures4/P1_05.eps}](img863.png) |
In the following, we will discuss the revised phase diagram shown in
Fig. ![[*]](crossref.png) . First of all, the nodal surfaces are not
important for low densities e.g.
. First of all, the nodal surfaces are not
important for low densities e.g.
![]() . Therefore, we can copy
the low density PIMC results using free particle nodes that determine
the location of the molecular and atomic regime. Furthermore, we
compare the histograms of the permutation probability shown in
Fig.
. Therefore, we can copy
the low density PIMC results using free particle nodes that determine
the location of the molecular and atomic regime. Furthermore, we
compare the histograms of the permutation probability shown in
Fig. ![[*]](crossref.png) with those from free particle nodes in
Fig.
with those from free particle nodes in
Fig. ![[*]](crossref.png) . Generally, one finds that the permutation
probability is reduced for VDM nodes and that the area of metallic
regime in the temperature-density plane has shrunk considerably. This
can be understood as follows. FP nodes are generated from maximally
delocalized orbitals. Therefore, they could favor delocalized states
and allow more permutations. VDM nodes include bound states and lead to
more localized orbitals, which consequently reduces the fraction of
permuting electrons. A comparison of the distribution of the cycle
length can be found in Fig.
. Generally, one finds that the permutation
probability is reduced for VDM nodes and that the area of metallic
regime in the temperature-density plane has shrunk considerably. This
can be understood as follows. FP nodes are generated from maximally
delocalized orbitals. Therefore, they could favor delocalized states
and allow more permutations. VDM nodes include bound states and lead to
more localized orbitals, which consequently reduces the fraction of
permuting electrons. A comparison of the distribution of the cycle
length can be found in Fig. ![[*]](crossref.png) . However, it should be
noted that there is the possibility that the VDM leads to too
localized orbitals in the limit of high density, as indicated by the
too small width of the Gaussians orbitals shown in Fig. 3.11.
. However, it should be
noted that there is the possibility that the VDM leads to too
localized orbitals in the limit of high density, as indicated by the
too small width of the Gaussians orbitals shown in Fig. 3.11.
|
In the next step, we calculated the pressure as a function of
temperature for ![]() using different time steps as in
Fig.
using different time steps as in
Fig. ![[*]](crossref.png) . Within the statistical error bars, results from
PIMC simulations with VDM nodes do not show a region where the
pressure drops down with increasing T,
. Within the statistical error bars, results from
PIMC simulations with VDM nodes do not show a region where the
pressure drops down with increasing T,
![]() . This shows that the results in
regime near the PPT are strongly affected by the type of nodes being
used. This also raises some concern on how reliable the PIMC
simulations are in this regime. However, one can proceed as is
done in QMC at
. This shows that the results in
regime near the PPT are strongly affected by the type of nodes being
used. This also raises some concern on how reliable the PIMC
simulations are in this regime. However, one can proceed as is
done in QMC at ![]() , where one takes those set of nodes
which leads to the lowest internal energy. At finite temperature, we
used the free energy argument above and concluded that the VDM nodes
are more reliable. They do not seem to predict a first order PPT in
the particular region of density and temperature shown in
Fig.
, where one takes those set of nodes
which leads to the lowest internal energy. At finite temperature, we
used the free energy argument above and concluded that the VDM nodes
are more reliable. They do not seem to predict a first order PPT in
the particular region of density and temperature shown in
Fig. ![[*]](crossref.png) . However, there is the possibility that
the PPT has been shifted to temperatures below
. However, there is the possibility that
the PPT has been shifted to temperatures below ![]() K and that the
metallic phase exhibits again a low temperature boundary, which is
characterized by a PPT similar to the metallic regime predicted
using free particle nodes as shown in Fig.
K and that the
metallic phase exhibits again a low temperature boundary, which is
characterized by a PPT similar to the metallic regime predicted
using free particle nodes as shown in Fig. ![[*]](crossref.png) . On
the other hand, one can say that the PPT might have disappeared
because we employed VDM nodes that includes a reasonable description
of bound states as well as free particle states and therefore, we got
rid of the imbalance that the free particle favored the metallic
regime.
. On
the other hand, one can say that the PPT might have disappeared
because we employed VDM nodes that includes a reasonable description
of bound states as well as free particle states and therefore, we got
rid of the imbalance that the free particle favored the metallic
regime.
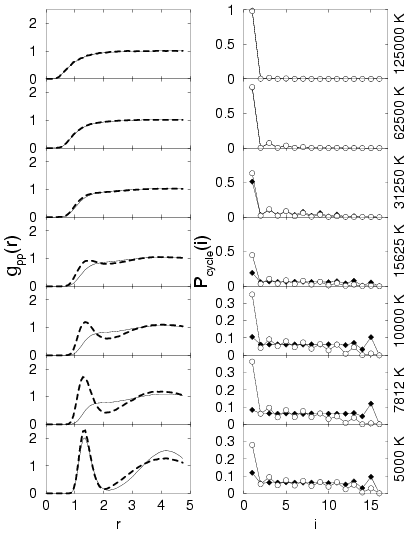
The PPT predicted by free particle nodes also predicted a change in
the number of molecules. In Fig. ![[*]](crossref.png) , the
proton-proton pair correlation functions as well as the permutation
cycle distributions are shown for series of simulations for different
temperatures at
, the
proton-proton pair correlation functions as well as the permutation
cycle distributions are shown for series of simulations for different
temperatures at ![]() . The two functions were chosen in order to
characterize the effect of the two different nodal surfaces. At high
temperatures such as
. The two functions were chosen in order to
characterize the effect of the two different nodal surfaces. At high
temperatures such as
![]() , simulations with FP and VDM
nodes give identical results because the nodes are equivalent in this
limit. At this temperature, hydrogen is composed of strongly
interacting gas of free protons and electrons with a moderate degree of
electronic degeneracy (
, simulations with FP and VDM
nodes give identical results because the nodes are equivalent in this
limit. At this temperature, hydrogen is composed of strongly
interacting gas of free protons and electrons with a moderate degree of
electronic degeneracy (
![]() ). With decreasing
temperature, the degeneracy increases, which can be inferred from cycle
distributions. At
). With decreasing
temperature, the degeneracy increases, which can be inferred from cycle
distributions. At
![]() , small deviations between FP
and VDM nodes emerge. At half the temperature, the differences have
increased further, which consequently lead to a different state with
different proton-proton pair correlations. Simulations with VDM nodes
predict a significant molecular fraction and a smaller degeneracy,
while FP results show no peak in the proton-proton pair correlation
function in combination with a larger degeneracy. In the FP case, most of
the electrons are delocalized and occupy states similar to a free Fermi
gas. VDM nodes predict that the electrons are in more localized
states, which leads to the molecular binding.
, small deviations between FP
and VDM nodes emerge. At half the temperature, the differences have
increased further, which consequently lead to a different state with
different proton-proton pair correlations. Simulations with VDM nodes
predict a significant molecular fraction and a smaller degeneracy,
while FP results show no peak in the proton-proton pair correlation
function in combination with a larger degeneracy. In the FP case, most of
the electrons are delocalized and occupy states similar to a free Fermi
gas. VDM nodes predict that the electrons are in more localized
states, which leads to the molecular binding.
|
At ![]() one finds big differences in the proton-proton pair
correlation functions since FP nodes predict a metallic state and VDM
nodes a more molecular structure. At
one finds big differences in the proton-proton pair
correlation functions since FP nodes predict a metallic state and VDM
nodes a more molecular structure. At ![]() both are rather
similar because according the FP nodes, one has crossed the phase
boundary, the pressure has risen and molecules are formed. VDM nodes, on
the other hand, predict a smooth transition.
both are rather
similar because according the FP nodes, one has crossed the phase
boundary, the pressure has risen and molecules are formed. VDM nodes, on
the other hand, predict a smooth transition.
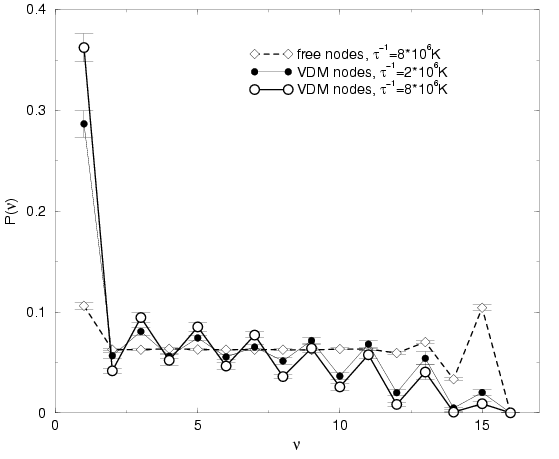
From Fig. ![[*]](crossref.png) , it can be deduced that the discussed
differences in the number of permutations are indeed a consequence of
the type of nodes rather than a result of using a too large time
step. Going from
, it can be deduced that the discussed
differences in the number of permutations are indeed a consequence of
the type of nodes rather than a result of using a too large time
step. Going from
![]() to
to
![]() reduces the number of permutations slightly because the nodal
surfaces are enforced more accurately, which prevents some
permutations from occurring. However, the differences to FP results are
significantly larger.
reduces the number of permutations slightly because the nodal
surfaces are enforced more accurately, which prevents some
permutations from occurring. However, the differences to FP results are
significantly larger.