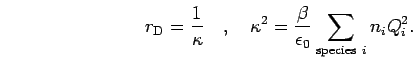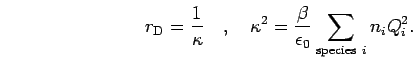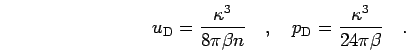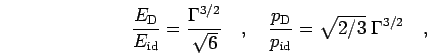Next: Equation of State Tables
Up: Path Integral Monte Carlo
Previous: Finite Temperature Jastrow Factor
Contents
Debye Model
At sufficiently high temperature and low density, the hydrogen plasma
behaves like a system of free electrons and protons, which interact
via a screened Coulomb potential (Ebeling et al., 1976; Fowler and Guggenheim, 1965). The screening
arises from a cloud of opposite charge of the size of the Debye radius
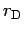 . Assuming full dissociation, it is given by,
. Assuming full dissociation, it is given by,
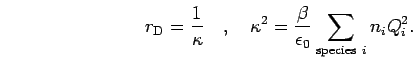 |
(269) |
The screening leads to the following corrections 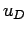 and
and 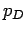 that are added internal
energy and pressure of non-interacting Fermi gas,
that are added internal
energy and pressure of non-interacting Fermi gas,
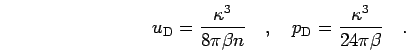 |
(270) |
If Fermi statistics is not important the Debye corrections can be expressed in the
terms of the coupling parameter 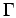 (Eq. 1.4),
(Eq. 1.4),
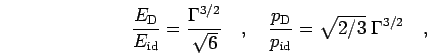 |
(271) |
where 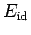 and
and 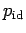 are the internal energy and pressure of a
ideal gas of distinguishable particles. The Debye screening represents
the first correction to the free particle behavior due to interactions
in the limit of high temperature and low density. For small values of
are the internal energy and pressure of a
ideal gas of distinguishable particles. The Debye screening represents
the first correction to the free particle behavior due to interactions
in the limit of high temperature and low density. For small values of
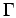 , the Debye model is a reliable approximation. One finds
deviations of less than
, the Debye model is a reliable approximation. One finds
deviations of less than 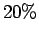 in pressure and energy for
in pressure and energy for 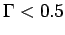 in discussed density range. However, at sufficiently high
in discussed density range. However, at sufficiently high
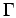 , the Debye model overestimates the screening drastically and
predicts a too small
, the Debye model overestimates the screening drastically and
predicts a too small 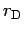 , which leads to unphysically low, even
negative pressures.
, which leads to unphysically low, even
negative pressures.




Next: Equation of State Tables
Up: Path Integral Monte Carlo
Previous: Finite Temperature Jastrow Factor
Contents
Burkhard Militzer
2003-01-15