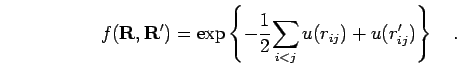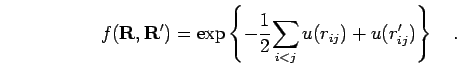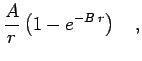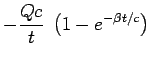


Next: Debye Model
Up: Path Integral Monte Carlo
Previous: Variational Interaction Terms
Contents
The VDM method can be improved by including correlations that are missed in an
Hartree-Fock type ansatz. This is usually done in form of a Jastrow factor f(R,R')
as shown in Eq. 3.79,
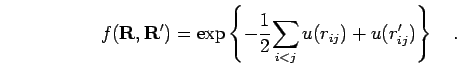 |
(263) |
The Jastrow factor can be calculated at zero temperature using the RPA
(see Ceperley and Alder (1981)), then generalized to finite temperature and
approximately expressed in the form (Pollock, 2000),
where 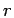 is the separation of the pair of particles. The coefficients
is the separation of the pair of particles. The coefficients
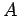 and
and 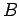 depend on density
depend on density 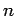 , inverse temperature
, inverse temperature 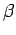 , and on
the type of interacting particles. They are derive that the fulfill
the cusp condition at any temperature. The coefficients for a pair of
electrons is given by,
, and on
the type of interacting particles. They are derive that the fulfill
the cusp condition at any temperature. The coefficients for a pair of
electrons is given by,
For an electron and an ion of charge 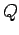 , they read,
, they read,



Next: Debye Model
Up: Path Integral Monte Carlo
Previous: Variational Interaction Terms
Contents
Burkhard Militzer
2003-01-15