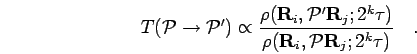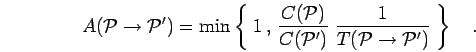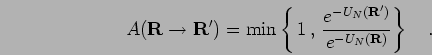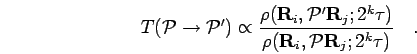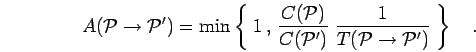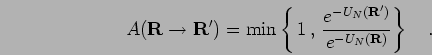Next: Variational Density Matrix Technique
Up: Fermion Nodes
Previous: Distribution of Permutation Cycles
Contents
Sampling Procedure
The sampling procedure used in the MC simulations consists of several
steps, which will be briefly described here,
- Select the time slices to be modified (
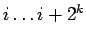 ) either at
random or by making random steps with an upper limit.
) either at
random or by making random steps with an upper limit.
- Build a permutation table containing up to 3 particle permutations
using the probability similar to Eq. 2.69
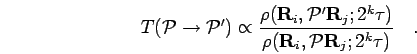 |
(115) |
This can be considered the zeroth step in the multilevel sampling
procedure. Dividing out the current permutation term has the advantage
that it lead to 100% acceptance for free particles in the following
first slice sampling step. In the case of fermions and close paths,
permutations of a even number of particles do not enter the table since
they will inevitably lead to a violation of the nodes.
- Determine the new midpoints given by
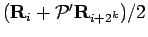 , sample
the new coordinates from Eq. 2.64 and accept with probability,
, sample
the new coordinates from Eq. 2.64 and accept with probability,
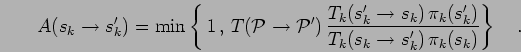 |
(116) |
We use only the diagonal part of the pair action at this level. Note
that for high levels where
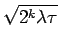 is of the order
of the box size, corrections to
is of the order
of the box size, corrections to  need to be considered because
points in the tail of the Gaussian fall out of the box and are mapped
back in by the periodic boundary conditions. This leads to additional
terms in the probability of sampling a particular point.
If this move of rejected here or at any later stage continue at step 2
or 1.
need to be considered because
points in the tail of the Gaussian fall out of the box and are mapped
back in by the periodic boundary conditions. This leads to additional
terms in the probability of sampling a particular point.
If this move of rejected here or at any later stage continue at step 2
or 1.
- Continue the bisection method based on Eq. 2.66
down to level 1. Consider the long-range as well as the off-diagonal
pair action only at the last level.
- Perform a Metropolis rejection step on the permutations by calculating
the probability for the reverse move,
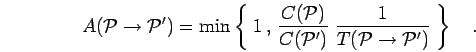 |
(117) |
The factor
![$\left[ T({\mathcal{P}}\to {\mathcal{P}}') \right]^{-1}$](img546.png) cancels with the extra term in
Eq. 2.107.
cancels with the extra term in
Eq. 2.107.
- Check the nodal surfaces in each slice, verify that
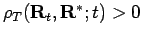 .
.
- Make a Metropolis rejection step based on the difference in the nodal action,
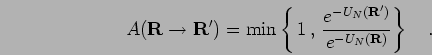 |
(118) |
- Upon final acceptance, update all coordinates. Continue at step 1 or 2.
Some averages are calculated at every step, others less frequently
e.g. only when one moves to a new section of the paths. In the MC
simulation, some displacement moves are intertwined with the
multilevel sampling moves described above. This completes the description
for a simulation with closed paths. The modifications
required for open paths are discussed in chapter
5.




Next: Variational Density Matrix Technique
Up: Fermion Nodes
Previous: Distribution of Permutation Cycles
Contents
Burkhard Militzer
2003-01-15