|
The distribution of permutation cycles has significant effects on the thermodynamics properties of the studied system since they represent the fermionic character. Here, we will discuss how it changes with increasing degeneracy.

|
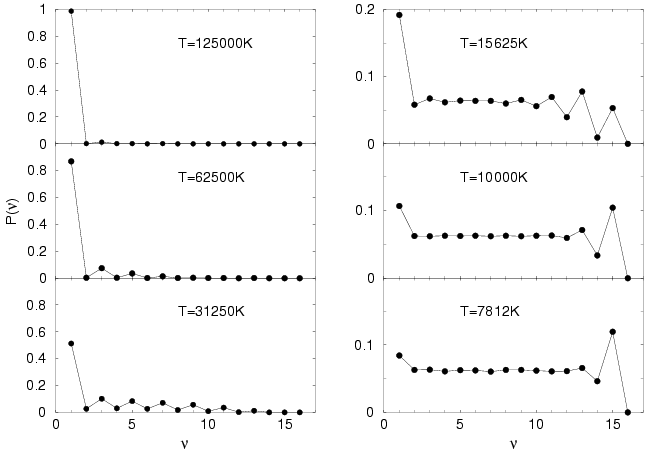
In Fig. 2.4, the probability distribution ![]() of
permutation cycles of different length
of
permutation cycles of different length ![]() from PIMC simulations are
shown. The normalization is given
from PIMC simulations are
shown. The normalization is given
![]() . We found that
the fraction of
. We found that
the fraction of ![]() -cycles
-cycles ![]() is a good candidate to discuss the
degree degeneracy. Beginning at
is a good candidate to discuss the
degree degeneracy. Beginning at ![]() in a non-degenerate system, it
decreases with increasing degeneracy. Simultaneously, states with
higher cycle lengths are populated. At first, odd cycles have a higher
probability, while one finds an almost uniform distribution at high
degeneracy. The reason is that the nodal surfaces prohibit even
permutations, which means an even number of even cycles must occur
simultaneously and more importantly within the distance of the order
of the thermal de Broglie wave length. It can be shown from the
determinant that isolated even cycles would violate the nodes. This is
also the reason why systems with even numbers of particles cannot form
one long chain (
in a non-degenerate system, it
decreases with increasing degeneracy. Simultaneously, states with
higher cycle lengths are populated. At first, odd cycles have a higher
probability, while one finds an almost uniform distribution at high
degeneracy. The reason is that the nodal surfaces prohibit even
permutations, which means an even number of even cycles must occur
simultaneously and more importantly within the distance of the order
of the thermal de Broglie wave length. It can be shown from the
determinant that isolated even cycles would violate the nodes. This is
also the reason why systems with even numbers of particles cannot form
one long chain (![]() in Fig. 2.4). At high
degeneracy where the thermal de Broglie wave length is larger than the
inter-particle spacing, the nodal constraint does not discriminate
between even and odd cycles.
in Fig. 2.4). At high
degeneracy where the thermal de Broglie wave length is larger than the
inter-particle spacing, the nodal constraint does not discriminate
between even and odd cycles.
This observed cycle distribution with fermion nodes is very different
from what one expects from direct fermion methods, where one considers
the signs explicitly and does not use nodal surfaces, e.g. the cycle
distribution of a system of non-interacting fermions can be calculated
in the grand canonical ensemble (Feynman, 1972). One has to differentiate
between odd and even cycle lengths leading to positive and negative
contributions to the partition function. Incorporating the sign into
![]() , it reads
, it reads
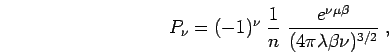 |
(114) |