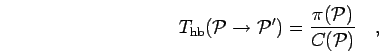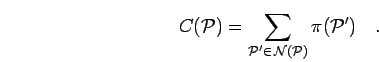Next: Fermion Nodes
Up: Monte Carlo Sampling
Previous: Multilevel Moves
Contents
Permutation Sampling
Fermi and Bose statistics require to sum over all permutations in
addition to the integration in real space. Both can be combined into
one MC process that samples configurations in the space of coordinates and
permutations.
In Eq. 2.47, one sums paths beginning at  and
going to
and
going to
 . One can also think of two sets of coordinates
. One can also think of two sets of coordinates
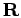 and
and 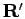 , for which one integrates over all possible ways to
link the individual particles. In this picture, the permutation of the
paths can be carried out at any time slice because the permutation
operator permutes with the Hamiltonian. This is what is done in the actual MC
simulation. One selects a time slice denoted by
, for which one integrates over all possible ways to
link the individual particles. In this picture, the permutation of the
paths can be carried out at any time slice because the permutation
operator permutes with the Hamiltonian. This is what is done in the actual MC
simulation. One selects a time slice denoted by
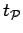 , at which one
switches from the unpermuted to the permuted coordinates.
, at which one
switches from the unpermuted to the permuted coordinates.
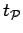 can
be shifted to any slice along the paths. In a permutation move, one
introduces a new permutation and simultaneously regrows the paths
between the fixed points
can
be shifted to any slice along the paths. In a permutation move, one
introduces a new permutation and simultaneously regrows the paths
between the fixed points 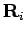 and
and 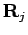 with
with 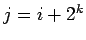 . The
equilibrium distribution of the permutation is given by,
. The
equilibrium distribution of the permutation is given by,
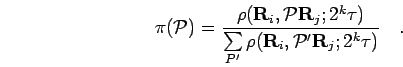 |
(78) |
Since there are 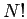 permutations, it is advisable to put an upper
limit on the step size in permutation space. Typically, one only
considers changes in current permutations that involve the cyclic
exchange of up to 3 or 4 particles. Since the normalization is known
in Eq. 2.69 one can use the heat bath
transition rule, in which a permutation
permutations, it is advisable to put an upper
limit on the step size in permutation space. Typically, one only
considers changes in current permutations that involve the cyclic
exchange of up to 3 or 4 particles. Since the normalization is known
in Eq. 2.69 one can use the heat bath
transition rule, in which a permutation
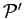 is sampled from the
neighborhood
is sampled from the
neighborhood
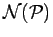 of the current permutation
of the current permutation 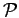 using their
equilibrium distribution,
using their
equilibrium distribution,
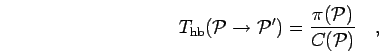 |
(79) |
where the normalization is given by the sum over all neighboring states,
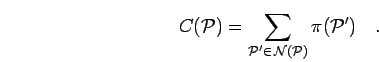 |
(80) |
The acceptance probability follows from Eq. 2.53,
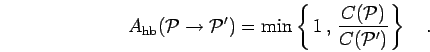 |
(81) |
If the neighborhoods of 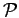 and
and
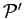 are equal, all moves will be
accepted. In the MC simulation, one uses the free particle density matrix to
construct a permutation table containing all permutations in the
neighborhood. Then
are equal, all moves will be
accepted. In the MC simulation, one uses the free particle density matrix to
construct a permutation table containing all permutations in the
neighborhood. Then
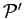 is selected and accepted with the
probability in Eq. 2.72, which does not exactly equal one
unless the permutation table exhausts the whole space.
is selected and accepted with the
probability in Eq. 2.72, which does not exactly equal one
unless the permutation table exhausts the whole space.




Next: Fermion Nodes
Up: Monte Carlo Sampling
Previous: Multilevel Moves
Contents
Burkhard Militzer
2003-01-15
![]() and
going to
and
going to
![]() . One can also think of two sets of coordinates
. One can also think of two sets of coordinates
![]() and
and ![]() , for which one integrates over all possible ways to
link the individual particles. In this picture, the permutation of the
paths can be carried out at any time slice because the permutation
operator permutes with the Hamiltonian. This is what is done in the actual MC
simulation. One selects a time slice denoted by
, for which one integrates over all possible ways to
link the individual particles. In this picture, the permutation of the
paths can be carried out at any time slice because the permutation
operator permutes with the Hamiltonian. This is what is done in the actual MC
simulation. One selects a time slice denoted by
![]() , at which one
switches from the unpermuted to the permuted coordinates.
, at which one
switches from the unpermuted to the permuted coordinates.
![]() can
be shifted to any slice along the paths. In a permutation move, one
introduces a new permutation and simultaneously regrows the paths
between the fixed points
can
be shifted to any slice along the paths. In a permutation move, one
introduces a new permutation and simultaneously regrows the paths
between the fixed points ![]() and
and ![]() with
with ![]() . The
equilibrium distribution of the permutation is given by,
. The
equilibrium distribution of the permutation is given by,