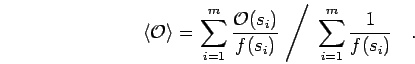Next: Single Slice Moves
Up: Monte Carlo Sampling
Previous: Monte Carlo Sampling
Contents
Most path integral calculations work with a Metropolis rejection
algorithm (Metropolis et al., 1953), in which a Markov process is constructed in
order to generate a random walk through state space,
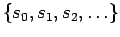 . A transition rule
. A transition rule
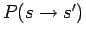 depending on the initial state
depending on the initial state 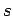 and
the final state
and
the final state 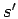 is exploited to step from
is exploited to step from 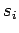 to
to
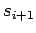 , which is chosen in such a way that the distribution of
, which is chosen in such a way that the distribution of
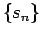 converges to a given distribution
converges to a given distribution 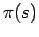 . If the
transition rule is ergodic and fulfills the detailed balance
. If the
transition rule is ergodic and fulfills the detailed balance
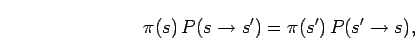 |
(59) |
then the probability distribution converges to an equilibrium
state satisfying,
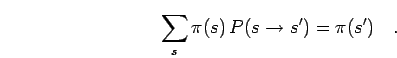 |
(60) |
The transition probability
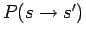 can be split
into two parts, the sampling distribution
can be split
into two parts, the sampling distribution 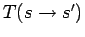 that
determines how the next trial state
that
determines how the next trial state 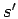 is selected in state
is selected in state
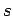 and the acceptance probability
and the acceptance probability 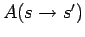 for the
particular step,
for the
particular step,
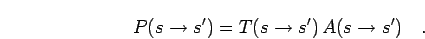 |
(61) |
The detailed balance can be satisfied by choosing 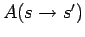 to be,
to be,
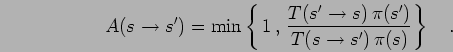 |
(62) |
One starts the MC process at any arbitrary state 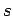 . Most likely
this state has only a very small probability because in thermodynamic system,
. Most likely
this state has only a very small probability because in thermodynamic system, 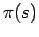 is
a sharply peaked function that usually spans many orders of
magnitude. Therefore, it would be overrepresented in averages
calculated from,
is
a sharply peaked function that usually spans many orders of
magnitude. Therefore, it would be overrepresented in averages
calculated from,
 |
(63) |
In the averages, one notices a transient behavior that eventually
reaches a regime, where it fluctuates around a steady mean. From
approximately that point on, one starts to collect statistics. For
uncorrelated measurements, the estimator for the standard deviation 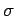 and the
error bars
and the
error bars 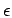 can be determined from
can be determined from
However, in most MC simulations the events are correlated because one
only moves a small fraction of the particles at a time. The correlation time 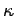 can be shown to be estimated by
can be shown to be estimated by
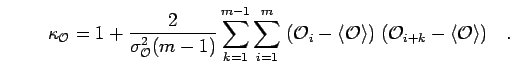 |
(66) |
The true statistical error considering correlations is given by
 |
(67) |
Alternatively, it can be obtained from a blocking
analysis. There, one averages over 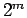 events
events
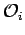 before
calculating the error bar from Eq. 2.56. This error will grow
as a function of
before
calculating the error bar from Eq. 2.56. This error will grow
as a function of 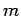 and eventually converge when the interval
and eventually converge when the interval 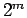 is long enough that the averages can be considered to be statistically
independent. It should be noted that there can be different reasons
for correlations in MC simulations that can occur on different time
scales. In certain cases, it becomes difficult to estimate the
correlation time from Eq. 2.55 because of long correlations
that can only be determine accurately from very long series of
simulations data.
is long enough that the averages can be considered to be statistically
independent. It should be noted that there can be different reasons
for correlations in MC simulations that can occur on different time
scales. In certain cases, it becomes difficult to estimate the
correlation time from Eq. 2.55 because of long correlations
that can only be determine accurately from very long series of
simulations data.
The aim of an efficient MC procedure is to decrease the error bars as
rapidly as possible for given computer time. The efficiency is defined
by,
 |
(68) |
where 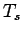 is the computer time per step.
is the computer time per step.
For certain applications, the sampling distribution 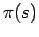 leads to
error bars for a subset of observables that are too large. A typical example
in classical MC is the pair correlation function
leads to
error bars for a subset of observables that are too large. A typical example
in classical MC is the pair correlation function 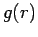 at small distances.
In those cases, importance sampling can be applied. One employs an
importance function
at small distances.
In those cases, importance sampling can be applied. One employs an
importance function 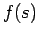 to generate a Markov chain according to modified
distribution
to generate a Markov chain according to modified
distribution
 |
(69) |
rather than to 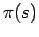 . In the end, one divides it out and calculates averages from
. In the end, one divides it out and calculates averages from
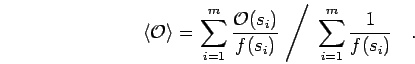 |
(70) |
This method will be applied to the sampling with open paths in chapter
5. It works well as long
as the modifications to the sampling distribution are not too
disruptive. Otherwise, the variance
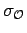 grows or even becomes
infinite. A sufficient condition for the applicability is that
grows or even becomes
infinite. A sufficient condition for the applicability is that
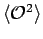 stays finite.
stays finite.




Next: Single Slice Moves
Up: Monte Carlo Sampling
Previous: Monte Carlo Sampling
Contents
Burkhard Militzer
2003-01-15
![]() . A transition rule
. A transition rule
![]() depending on the initial state
depending on the initial state ![]() and
the final state
and
the final state ![]() is exploited to step from
is exploited to step from ![]() to
to
![]() , which is chosen in such a way that the distribution of
, which is chosen in such a way that the distribution of
![]() converges to a given distribution
converges to a given distribution ![]() . If the
transition rule is ergodic and fulfills the detailed balance
. If the
transition rule is ergodic and fulfills the detailed balance
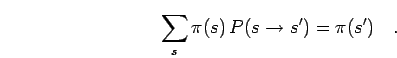

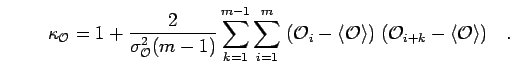

![]() leads to
error bars for a subset of observables that are too large. A typical example
in classical MC is the pair correlation function
leads to
error bars for a subset of observables that are too large. A typical example
in classical MC is the pair correlation function ![]() at small distances.
In those cases, importance sampling can be applied. One employs an
importance function
at small distances.
In those cases, importance sampling can be applied. One employs an
importance function ![]() to generate a Markov chain according to modified
distribution
to generate a Markov chain according to modified
distribution