In classical MC, the particles are represented by points in ![]() dimensional space, which are moved in every MC step. Most simply, one
can choose the displacement of particles according to a uniform
distribution. In PIMC, particles are represented by path and the
equivalent moves would shift the entire polymer to a new position
without changing its internal structure. We call this displacement moves and use them for the protons because their paths
stay very localized. They are more efficient than single or
multi-slice moves discussed in the following.
dimensional space, which are moved in every MC step. Most simply, one
can choose the displacement of particles according to a uniform
distribution. In PIMC, particles are represented by path and the
equivalent moves would shift the entire polymer to a new position
without changing its internal structure. We call this displacement moves and use them for the protons because their paths
stay very localized. They are more efficient than single or
multi-slice moves discussed in the following.
In a single slice move, one selects a particle and a time slice ![]() and samples a new configuration
and samples a new configuration ![]() while keeping
while keeping ![]() and
and
![]() fixed. From now on, the subscript denotes the time
slice. The optimal choice for the sampling distribution of
fixed. From now on, the subscript denotes the time
slice. The optimal choice for the sampling distribution of ![]() is
given by the heat bath rule, which will be described in section
2.5.4. It states that
the new coordinate should by chosen according to its equilibrium
distribution,
is
given by the heat bath rule, which will be described in section
2.5.4. It states that
the new coordinate should by chosen according to its equilibrium
distribution,
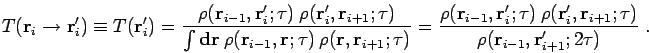 |
(71) |