An interesting new approach was proposed by Bando el al. [10] who
modeled the traffic flow in one dimension by solving an
equation of motion for each individual car,
denotes the position of vehicle number n (
).
This is a special case of the follow-the-leader theory (see [1]).
It is assumed that there exists a legal velocity 
, which
depends on the distance to the preceding vehicle. If this distance
becomes too small the velocity must be reduced in order to prevent a crash.
On the other hand, if the distance increases the vehicle can accelerate
until it reaches a given speed limit. Thus, has to be
a monotonically increasing function, which satisfies V(0)=0 and
.
is given by the fundamental diagram. Its functional form
plays a crucial role in
the dynamics of the traffic flow. This can be understood by studying
the stability of the steady state solution of of Eq. 9,
A stability analysis shows that this solution is only stable if
In [10], it has been suggested to choose,
and set a=1. This function leads to a realistic behavior of the traffic flow.
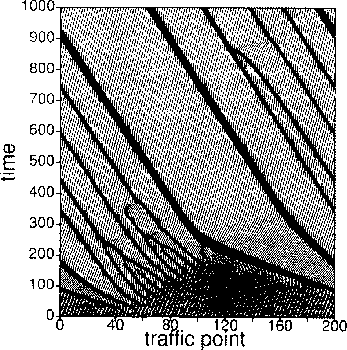
Figure 6:
The formation of traffic jams modeled by Bando el al. [10]. The position
of the vehicles are shown as function of time. The initially uncongested flow
soon develops small jams, which merge later.
The steady state solution is unstable for 1.12 < s < 2.88 and stable otherwise. This leads to two stable flow regimes, a low densities phase with fast moving vehicles in large separations and a congested phase with slowly moving cars at short distances. Both phases can be identified in Fig. 6 showing the evolving flow. The steady state solution in unstable regime with a small perturbation was chosen as the initial condition. At the beginning, several small jams form, which later merge to bigger congested phases. These move slowly in opposite direction to the cars, which travel at a high velocity from jam to jam. This scenario represents a stop-and-go behavior.