Fluid-dynamic approaches have been developed since the 1950's [2].
The road traffic is modeled as a one-dimensional compressible flow
with density 
with velocity v(x,t). The continuity equation
reads,
The dynamics can be expressed by the Navier-Stokes equation [3],
which states that the particle density times acceleration equals
the sum of the acting forces,
where p is the local pressure of the vehicular gas, 
is the viscosity and
X represents the force caused by the interaction of the individual vehicles.
The forces are derived from the density dependence of the velocity given by
the fundamental diagram such as shown in Fig. 2,
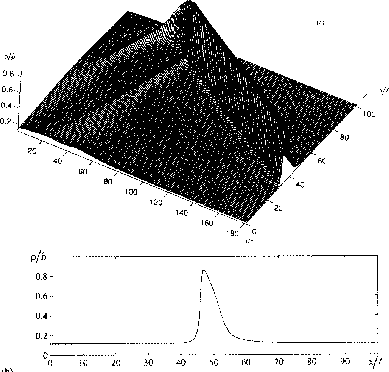
Figure 3: Time evolution of a traffic jam showing the density
upper graph and 
for a particular time (taken from [3]).
where 
is the relaxation time of the process. Kerner el al.
[3, 4, 5] showed that
this ansatz leads to the formation of stationary clusters (jams). Their
form is shown in Fig. 3.
The model was significantly improved by Helbing [6] who introduced
the variance of the velocities as an additional space and time dependent
variable. He showed the this approach leads to a more realistic behavior
when jams develop.