



Next: Improvements in the Nodal
Up: Fermion Nodes
Previous: Example: Nodes for Two
Contents
In restricted PIMC simulation, one enforces the node by checking the
sign of the determinant at each time slice. If it turns out to be
negative for a proposed configuration, the move is rejected. The nodes
act like an infinite potential barrier. In this method, it is
implicitly assumed that the paths do not wander too far between the
slices and in particular do not cross a node. This puts an additional
lower bound on the number of slices used in a simulation in order to
enforce the nodes accurately. By inserting additional slices, one
finds that the some paths are rejected on the finer scale, which could
not have been detected earlier because they crossed and recrossed the node
within the slice. This error can be corrected for by introducing the
nodal action 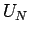 .
.
One assumes a flat node between two slices like in the example discussed
in the previous section, which is a reasonable approximation for small
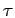 . The difference in action between a system containing a node
compared to one without it can be expressed as,
. The difference in action between a system containing a node
compared to one without it can be expressed as,
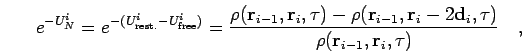 |
(101) |
where 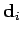 is the distance to the nearest node at the time slice
is the distance to the nearest node at the time slice
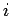 . The image charge is placed at
. The image charge is placed at
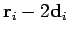 . Using the free
particle density matrix, the nodal action can be written in terms
of the distances to the node at the two slices,
. Using the free
particle density matrix, the nodal action can be written in terms
of the distances to the node at the two slices,
![\begin{displaymath}
e^{-U_N^i} = 1- \exp \, [ \: - \: d_i \, d_{i-1}\:/ \, \lambda \tau \, ]
\quad.
\end{displaymath}](img489.png) |
(102) |
The distance is difficult to calculate but it can be estimated using
Newton-Raphson procedure,
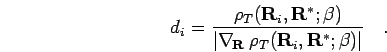 |
(103) |
If 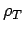 is given in matrix form
is given in matrix form
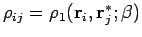 ,
its derivatives (denoted by
,
its derivatives (denoted by 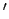 ) can be calculated efficiently from the cofactor
matrix (its transposed inverse)
) can be calculated efficiently from the cofactor
matrix (its transposed inverse)
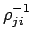 ,
,
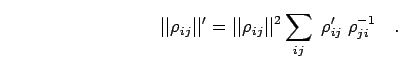 |
(104) |
The distance to the node then reads,
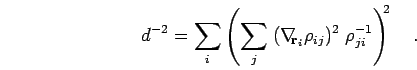 |
(105) |
The additional term in the action 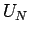 also leads to a contribution to the
internal energy, which can be derived from
also leads to a contribution to the
internal energy, which can be derived from
The time derivative of 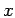 can be approximated by,
can be approximated by,
This approximation omits the change in the distance to the node with
imaginary time. It has the advantage that one does not have to compute
the derivatives of the distance to the nearest node 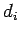 , which would
require extra numerical work.
, which would
require extra numerical work.
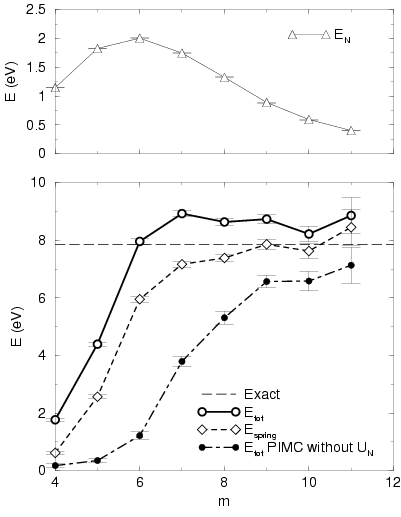
Figure 2.2:
Comparison of the internal energy per electron from two simulations, one with nodal action (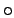 )
and one without (
)
and one without ( ), for 16 free particles at
), for 16 free particles at 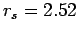 and
and
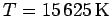 for different number of time slices
for different number of time slices 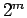 leading to
a time step
leading to
a time step
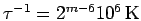 .
.  shows the
nodal energy and
shows the
nodal energy and  denotes the spring kinetic energy given
by
denotes the spring kinetic energy given
by 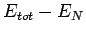 . The long dashed line shows the exact energy for this
finite system. All simulations were
. The long dashed line shows the exact energy for this
finite system. All simulations were 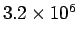 steps of level
steps of level 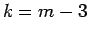 long.
long.
|
|
The effect of the nodal action 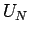 is shown in Fig. 2.2,
where two simulations, one with it and without it, are compared as a
function of time step. In these simulations,
is shown in Fig. 2.2,
where two simulations, one with it and without it, are compared as a
function of time step. In these simulations, 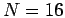 spin-polarized
free electrons were studied at
spin-polarized
free electrons were studied at
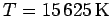 and
and 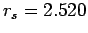 . The
conditions were chosen in correspondence with hydrogen
simulations discussed in chapter
. The
conditions were chosen in correspondence with hydrogen
simulations discussed in chapter
![[*]](crossref.png) where 32 protons and 32
electrons in two spin states are studied at a typical density
corresponding to
where 32 protons and 32
electrons in two spin states are studied at a typical density
corresponding to 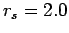 . The Fermi temperature for an infinite
system (Eq. 2.74) under these conditions is
. The Fermi temperature for an infinite
system (Eq. 2.74) under these conditions is
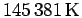 . For
a system with
. For
a system with 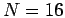 , it becomes
, it becomes
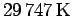 . The difference is
that large because the only 3
. The difference is
that large because the only 3 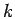 -shells are occupied while in
Eq. 2.74 sum of k-shells were approximated by an integral. The
number of states per k-shell starting from
-shells are occupied while in
Eq. 2.74 sum of k-shells were approximated by an integral. The
number of states per k-shell starting from 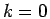 are 1, 6, 12, 8, 6, 24, ...
are 1, 6, 12, 8, 6, 24, ...
All hydrogen simulations discussed later are performed with
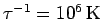 (64 slices,
(64 slices, 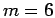 ) or smaller time steps. The required
time step can be estimated from the corresponding degeneracy
parameter,
) or smaller time steps. The required
time step can be estimated from the corresponding degeneracy
parameter,
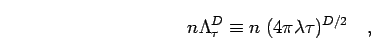 |
(110) |
which relates the average distance the path travels between the slices,
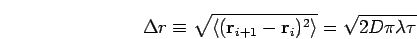 |
(111) |
to the inter-particle spacing. For the above example with
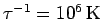 , one finds
, one finds
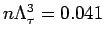 and
and
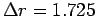 , which must be compared to the inter-particle spacing given by
, which must be compared to the inter-particle spacing given by
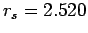 . For the example of
. For the example of 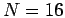 particles at this
degeneracy, Fig. 2.2 predicts that choosing the time
step such that
particles at this
degeneracy, Fig. 2.2 predicts that choosing the time
step such that
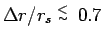 (
(
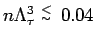 ) leads to energies reasonably close to the exact value. To go up
to 2048 slices (
) leads to energies reasonably close to the exact value. To go up
to 2048 slices (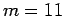 ) is only possible for a system of free particles
this small. The figure shows clearly that in simulations with the
nodal action term, the internal energy converges faster to the exact
value of 7.844 eV, the reason being that configurations of paths where
the nodal constraints are likely to be violated between the slices are
rejected because of the
) is only possible for a system of free particles
this small. The figure shows clearly that in simulations with the
nodal action term, the internal energy converges faster to the exact
value of 7.844 eV, the reason being that configurations of paths where
the nodal constraints are likely to be violated between the slices are
rejected because of the 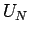 term. However, the graph also shows that
the nodal energy is overestimated leading to an internal energy 10%
too large. Possible explanations for this discrepancy include the
approximations in the way the distance to the node is estimated, the
implicit assumption that the nodes are planar within the time interval
term. However, the graph also shows that
the nodal energy is overestimated leading to an internal energy 10%
too large. Possible explanations for this discrepancy include the
approximations in the way the distance to the node is estimated, the
implicit assumption that the nodes are planar within the time interval
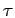 and the omission of two terms in
Eq. 2.99. However, in the limit of small
and the omission of two terms in
Eq. 2.99. However, in the limit of small 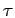 all
those approximations do not matter and one should find the above
mentioned exact value, which was calculated by a separate MC method in
all
those approximations do not matter and one should find the above
mentioned exact value, which was calculated by a separate MC method in
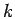 -space. The nodal constraint there is realized by restricting each
-space. The nodal constraint there is realized by restricting each
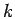 -point to only one particle. However, the method relies on the
exactly known eigenstates of the Hamiltonian.
-point to only one particle. However, the method relies on the
exactly known eigenstates of the Hamiltonian.




Next: Improvements in the Nodal
Up: Fermion Nodes
Previous: Example: Nodes for Two
Contents
Burkhard Militzer
2003-01-15
![]() .
.
![]() . The difference in action between a system containing a node
compared to one without it can be expressed as,
. The difference in action between a system containing a node
compared to one without it can be expressed as,
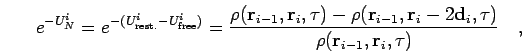
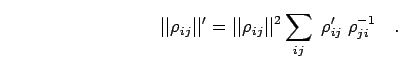
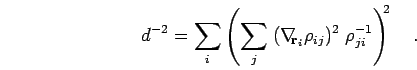
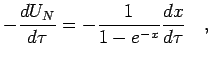
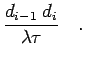
![]() is shown in Fig. 2.2,
where two simulations, one with it and without it, are compared as a
function of time step. In these simulations,
is shown in Fig. 2.2,
where two simulations, one with it and without it, are compared as a
function of time step. In these simulations, ![]() spin-polarized
free electrons were studied at
spin-polarized
free electrons were studied at
![]() and
and ![]() . The
conditions were chosen in correspondence with hydrogen
simulations discussed in chapter
. The
conditions were chosen in correspondence with hydrogen
simulations discussed in chapter
![[*]](crossref.png) where 32 protons and 32
electrons in two spin states are studied at a typical density
corresponding to
where 32 protons and 32
electrons in two spin states are studied at a typical density
corresponding to ![]() . The Fermi temperature for an infinite
system (Eq. 2.74) under these conditions is
. The Fermi temperature for an infinite
system (Eq. 2.74) under these conditions is
![]() . For
a system with
. For
a system with ![]() , it becomes
, it becomes
![]() . The difference is
that large because the only 3
. The difference is
that large because the only 3 ![]() -shells are occupied while in
Eq. 2.74 sum of k-shells were approximated by an integral. The
number of states per k-shell starting from
-shells are occupied while in
Eq. 2.74 sum of k-shells were approximated by an integral. The
number of states per k-shell starting from ![]() are 1, 6, 12, 8, 6, 24, ...
are 1, 6, 12, 8, 6, 24, ...
![]() (64 slices,
(64 slices, ![]() ) or smaller time steps. The required
time step can be estimated from the corresponding degeneracy
parameter,
) or smaller time steps. The required
time step can be estimated from the corresponding degeneracy
parameter,