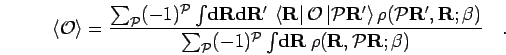Next: Restricted Path Integrals
Up: Fermion Nodes
Previous: Fermion Nodes
Contents
In simulations of fermionic systems, one has to deal with an extra
complication emerging from the cancellation of positive and negative
contributions to the averages calculated from,
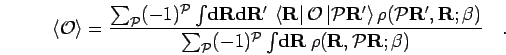 |
(82) |
Even permutations have positive signs and odd ones have negative
signs. The magnitude of the contributions from non-identity
permutations depends on the degeneracy of the systems, which can be
discussed in terms of the parameter 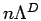 or equivalently as
the ratio of temperature to Fermi temperature
or equivalently as
the ratio of temperature to Fermi temperature 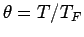 . Here, we
compare to the Fermi energy
. Here, we
compare to the Fermi energy 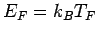 of an ideal quantum gas in 3
dimensions,
of an ideal quantum gas in 3
dimensions,
 |
(83) |
where 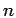 is the density of particles in this particular spin state,
which leads to
is the density of particles in this particular spin state,
which leads to
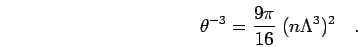 |
(84) |
If the temperature is of the order of the 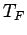 non-identity
permutations or lower are important. Those also lead to a significant
fraction of negative contributions to the enumerator as well as to the
denominator in Eq. 2.73. The consequence are large
fluctuations in the computed averages. This is known as the fermion sign problem. While Eq. 2.73 always leads to
the exact answer it becomes numerically increasingly difficult to
compute the averages at the point where the interesting fermionic
effects start to occur. It was shown by Ceperley (1996) that the
efficiency of the straightforward implementation scales like
non-identity
permutations or lower are important. Those also lead to a significant
fraction of negative contributions to the enumerator as well as to the
denominator in Eq. 2.73. The consequence are large
fluctuations in the computed averages. This is known as the fermion sign problem. While Eq. 2.73 always leads to
the exact answer it becomes numerically increasingly difficult to
compute the averages at the point where the interesting fermionic
effects start to occur. It was shown by Ceperley (1996) that the
efficiency of the straightforward implementation scales like
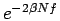 , where
, where 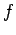 is the free energy difference per particle of a
corresponding fermionic and bosonic system while
is the free energy difference per particle of a
corresponding fermionic and bosonic system while 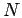 is the number of
particles.
is the number of
particles.




Next: Restricted Path Integrals
Up: Fermion Nodes
Previous: Fermion Nodes
Contents
Burkhard Militzer
2003-01-15