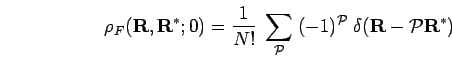Next: Trial Density Matrix
Up: Fermion Nodes
Previous: Fermion Sign Problem
Contents
Restricted Path Integrals
In the work by Ceperley (1996,1991), it has been shown that one can
evaluate the path integral by restricting the path to only specific
positive contributions. One introduces a reference point 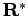 on
the path that specifies the nodes of the density matrix,
on
the path that specifies the nodes of the density matrix,
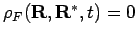 . A node-avoiding path for
. A node-avoiding path for
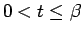 neither touches nor crosses a node:
neither touches nor crosses a node:
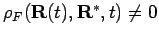 . By restricting the integral to node-avoiding paths,
. By restricting the integral to node-avoiding paths,
where
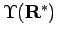 denotes the nodal restriction with respect to
the reference point
denotes the nodal restriction with respect to
the reference point 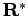 . The nodal restriction remains the same if
any permutation
. The nodal restriction remains the same if
any permutation 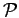 is applied to the reference point, which leads
to
is applied to the reference point, which leads
to
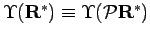 because
because
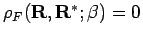 implies
implies
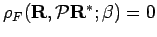 . Eq. 2.77 can now be written in the following alternative form,
. Eq. 2.77 can now be written in the following alternative form,
where we have applied the permutation
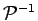 to the entire path
and changed the summation index using that the sign of
to the entire path
and changed the summation index using that the sign of 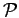 and
and
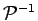 are equal.
are equal.
In the case of diagonal density matrix elements, Eq. 2.79 can
be simplified because odd permutations inevitably cross a node since
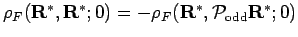 .
Eq. 2.79 then reads,
.
Eq. 2.79 then reads,
![\begin{displaymath}
\rho_F({\bf R}, {\bf R};\beta) = \frac{1}{N!}\; \sum_{{\math...
...! \! \! \! \!
{\bf d}{\bf R}_t \;\; e^{-S[{\bf R}_t] }\quad.
\end{displaymath}](img440.png) |
(89) |
For off-diagonal density matrix elements however, odd
permutations need to be considered and lead to negative contributions,
which will be discussed in chapter
5.
Since all contributions to the diagonal density matrix elements are
positive the restricted PIMC technique represents, in
principle, a solution to the sign problem. The method is exact if the
exact fermionic density matrix is used in the restriction. The proof
given by Ceperley (1996) consists of three steps.
- (i)
- The initial
condition for the Bloch equation 2.13 are given by,
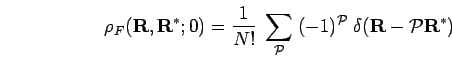 |
(90) |
and
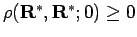 .
. 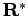 and therefore the initial
conditions are kept fixed for the following arguments. The
solution of the Bloch equation is uniquely determined by the boundary
conditions, which means
and therefore the initial
conditions are kept fixed for the following arguments. The
solution of the Bloch equation is uniquely determined by the boundary
conditions, which means
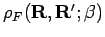 can be derived from
the values on a certain boundary
can be derived from
the values on a certain boundary
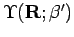 for all
for all
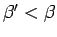 .
.
- (ii)
- The nodes of
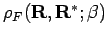 carve the space-time into a finite number
(
carve the space-time into a finite number
(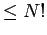 ) of nodal cells, that are sets of points in the space-time connected by
node-avoiding paths. From (i), it follows that the solution inside each nodal cell
can be constructed from the initial condition and the zero boundary condition
on the surface, which is determined by the nodes.
) of nodal cells, that are sets of points in the space-time connected by
node-avoiding paths. From (i), it follows that the solution inside each nodal cell
can be constructed from the initial condition and the zero boundary condition
on the surface, which is determined by the nodes.
- (iii)
- Enforcing zero boundary conditions at the nodes can be done by
introducing a infinite repulsive potential on the nodes, which
prevents any paths from crossing and therefore guarantees that the density matrix
vanishes at the cell boundaries.




Next: Trial Density Matrix
Up: Fermion Nodes
Previous: Fermion Sign Problem
Contents
Burkhard Militzer
2003-01-15
![]() on
the path that specifies the nodes of the density matrix,
on
the path that specifies the nodes of the density matrix,
![]() . A node-avoiding path for
. A node-avoiding path for
![]() neither touches nor crosses a node:
neither touches nor crosses a node:
![]() . By restricting the integral to node-avoiding paths,
. By restricting the integral to node-avoiding paths,
![]() .
Eq. 2.79 then reads,
.
Eq. 2.79 then reads,