



Next: Example: Nodes for Two
Up: Fermion Nodes
Previous: Trial Density Matrix
Contents
The Reference Point
The FP nodes as well as the VDM nodes represent approximations to the
exact fermion nodes that become increasingly accurate for high
temperatures. There is a simple trick that uses two reference points
instead of one and allows to enforce the nodes by taking the sign of
the trial density matrix from
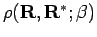 rather than from
rather than from
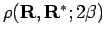 .
.
The density matrix
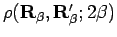 can be
expressed in terms of the convolution equation,
can be
expressed in terms of the convolution equation,
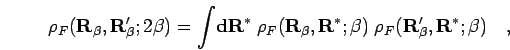 |
(93) |
which can be interpreted as an integral over all pairs of paths, one
going from 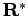 to
to 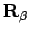 and a second one from
and a second one from 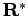 to
to
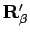 . Both fermion density matrices can evaluated using a
restricted path integral with the same reference point
. Both fermion density matrices can evaluated using a
restricted path integral with the same reference point 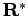 . This
requires the time argument to be zero at
. This
requires the time argument to be zero at 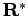 and to increase in
both directions up to
and to increase in
both directions up to 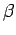 at
at 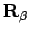 and
and
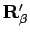 . Using
the explicit form of
. Using
the explicit form of 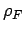 in Eq. 2.77 the above equation
becomes,
in Eq. 2.77 the above equation
becomes,
where we have employed the equivalence of Eq. 2.77 and
2.79 and also the fact that the double sum over permutations be converted
into a single one because the following path integral can be treated as two
independent factors. This expression can be interpreted as a single
path integral of the form
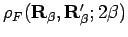 . The
paths start at
. The
paths start at 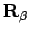 , goes through the reference
, goes through the reference 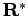 at the
middle of the path, and ends at
at the
middle of the path, and ends at
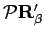 . The time argument to
check the nodes gets chosen according to,
. The time argument to
check the nodes gets chosen according to,
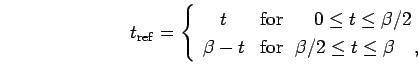 |
(97) |
which means one only needs to evaluate the trial density matrix up to
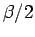 . This time doubling procedure cannot be applied further
without reintroducing the sign problem.
. This time doubling procedure cannot be applied further
without reintroducing the sign problem.




Next: Example: Nodes for Two
Up: Fermion Nodes
Previous: Trial Density Matrix
Contents
Burkhard Militzer
2003-01-15
![]() rather than from
rather than from
![]() .
.
![]() can be
expressed in terms of the convolution equation,
can be
expressed in terms of the convolution equation,
![$\displaystyle \frac{1}{{N!}^{\,2}} \int {\bf d}{\bf R}^*
\sum_{{\mathcal{P}}{\m...
...\! \! \! \! \! \! \! \! \! \! \! \! \!
{\bf d}{\bf R}_t \;\; e^{-S[{\bf R}_t] }$](img463.png)
![$\displaystyle \frac{1}{{N!}^{\,2}} \;
\sum_{{\mathcal{P}}{\mathcal{P}}'} \; (-1...
...\! \! \! \! \! \! \! \! \! \! \! \! \!
{\bf d}{\bf R}_t \;\; e^{-S[{\bf R}_t] }$](img464.png)
![$\displaystyle \frac{1}{{N!}} \;
\sum_{{\mathcal{P}}} \; (-1)^{{\mathcal{P}}} \;...
...\! \! \! \! \! \! \! %\! \! \!
{\bf d}{\bf R}_t \;\; e^{-S[{\bf R}_t] }
\quad,$](img465.png)