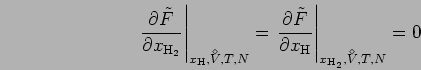Next: Computational Methods
Up: Introduction
Previous: Experimental Applications
Contents
Free Energy Models
There are two conceptually different approaches to describe hydrogen
and related materials. One method is based on the physical
picture where one treats the fundamental particles, in this case
electrons and proton, individually and compound particles such as
atoms and molecules are formed if the fundamental particle are bound
together. In PIMC, this approach is used, which has the advantage that
one can build a simulation from first principles that allows one to
describe regimes where one has a mixture of different species without
any additional assumptions. However, it should be noted that the
computational requirements are orders of magnitude higher than in the
chemical models described in the following.
In the chemical picture, one assumes different chemical
species. For hydrogen one usually considers molecules (H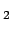 ), atoms
(H), free protons (p), and electrons (e). Other species such as
H
), atoms
(H), free protons (p), and electrons (e). Other species such as
H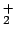 , H
, H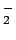 or H
or H are neglected, because their binding energies
are very small compared to the thermal energy. For the chemical
species under consideration, one constructs a free energy
function with the particle numbers
are neglected, because their binding energies
are very small compared to the thermal energy. For the chemical
species under consideration, one constructs a free energy
function with the particle numbers
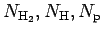 , and
, and 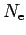 as
parameters.
as
parameters.
where the superscripts 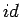 and
and 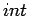 denote the ideal contribution
from non-interacting particles and the part caused by the
interactions. The interaction terms are derived from known analytical
expressions or from computer simulations. The subscripts
denote the ideal contribution
from non-interacting particles and the part caused by the
interactions. The interaction terms are derived from known analytical
expressions or from computer simulations. The subscripts 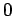 and
and
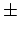 refer to neutral and charged. Introduce the total particle number,
refer to neutral and charged. Introduce the total particle number,
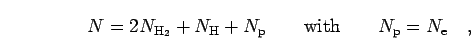 |
(6) |
one can define the number concentration 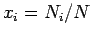 . The free energy
is maximized with respect to the chemical composition under fixed
external conditions, here temperature and volume. This lead to the
condition for chemical equilibrium of dissociation
H
. The free energy
is maximized with respect to the chemical composition under fixed
external conditions, here temperature and volume. This lead to the
condition for chemical equilibrium of dissociation
H
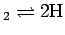 and ionization H
and ionization H
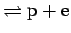 :
:
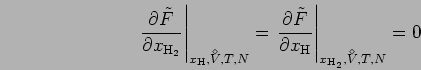 |
(7) |
with
![$\tilde{F}({V^{\!\!\!\!\!\!\:^\diamond}},T,N,x_{{\rm H}_2},x_{\rm H}) = F({V^{\!...
..._2},N x_{\rm H},
N_{\rm p}=N[1-2 x_{{\rm H}_2}-x_{\rm H}], N_{\rm e}=N_{\rm p})$](img216.png) . In terms of the chemical potentials,
. In terms of the chemical potentials,
 |
(8) |
chemical equilibrium is obtained from,
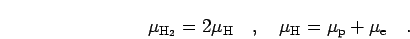 |
(9) |
Chemical models are known to work very well in regimes of weak
interaction between the different species. This is usually called the
Saha limit because the ideal Saha equation (Fowler and Guggenheim, 1965), which
neglects interaction between particles, gives a reasonable
approximation. The free energy models currently used to predict
properties of hydrogen employ elaborate schemes to determine the
interaction terms. Not all of them were constructed to describe the
whole high temperature phase diagram as done by
Saumon and Chabrier (1992). Ebeling and Richert (1985b) studied the plasma and the atomic
regime, while models by Beule et al. (1999) and Bunker et al. (1997) were designed to
the describe the dissociation transition. The Ross (1998) model was
primarily developed to study the molecular-metallic transition. One
difficulty common to free energy models is how to treat the
interaction of charged and neutral particles. Often, this is done by
introducing hard-sphere radii and additional corrections. These kinds
of approximation lead to rather different predictions from various
chemical models. The differences are especially pronounced in the
regime of the molecular-metallic transition because of the high
density and the presence of neutral and charged species. If the
derivative of the free energy function is a continuous function in
this region, then no PPT is predicted. If on the other hand the
different components in 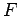 lead to a discontinuous first derivative,
a PPT is inevitably predicted.
lead to a discontinuous first derivative,
a PPT is inevitably predicted.
One purpose of our PIMC calculation is to provide data so that free
energy models can be fitted to it. Those can then be used to derive
additional information, which can not be obtained directly from PIMC
simulations.




Next: Computational Methods
Up: Introduction
Previous: Experimental Applications
Contents
Burkhard Militzer
2003-01-15
![]() ), atoms
(H), free protons (p), and electrons (e). Other species such as
H
), atoms
(H), free protons (p), and electrons (e). Other species such as
H![]() , H
, H![]() or H
or H![]() are neglected, because their binding energies
are very small compared to the thermal energy. For the chemical
species under consideration, one constructs a free energy
function with the particle numbers
are neglected, because their binding energies
are very small compared to the thermal energy. For the chemical
species under consideration, one constructs a free energy
function with the particle numbers
![]() , and
, and ![]() as
parameters.
as
parameters.