Notations

BRW

Brownian random walk,

DE

Direct estimator,

EOS

Equation of state,

FP

Free particle,

MC

Monte Carlo,

PIMC

Path integral Monte Carlo,

PPT

Plasma phase transition,

RPA

Random Phase Approximation,

TE

Thermodynamic estimator,

VDM

Variational density matrix,

$a$

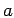
Wigner-Seitz radius,

$a_0$

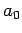
Electron Bohr radius,

$A(s\to s')$

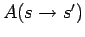
Acceptance probability for MC step $s\to s'$,

$\beta$

$1/ k_B T$,

$D$

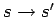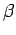
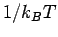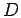
Spatial dimension, here 3,

$d$

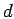
Amplitude parameter in Gaussian density matrix,

$E$

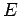
Internal energy per atom,

$E_i$

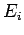
Internal energy of state $i$,

$E_F$

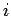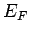
Fermi energy,

$F$

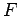
Free energy,

$g_{ij}(r)$

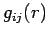
Pair distribution function of species 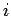$i$ and $j$,

$\lambda$

$\hbar^2/2m$,

$\Lambda$

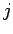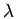
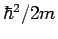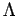
Thermal de Broglie wave length $\sqrt{4 \pi \lambda \beta}$,

$\mathcal{K}$

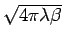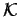
Kinetic energy operator,

$K$

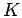
Kinetic energy function,

$\mathbf{k}$

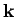
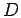$D$ dimensional reciprocal lattice vector,

$k_B$

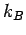
Boltzmann factor,

$M$

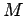
Number of time slices,

${\bf m}$

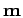
Position vector in Gaussian density matrix,

$n$

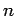
Number of particles per unit volume, for hydrogen atoms per unit volume,

$\mathbf{n}$

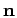
Integer vector in 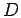$D$ dimensions,

$N$

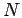
Number of particles,

$n_{\rm A}$

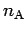
Order in expansion formula 2.38 used to calculate the pair action,

$n_{\rm E}$

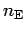
Order in corresponding expansion formula 2.38 for the energy,

$n(k)$

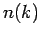
Momentum distribution,

$n(r)$

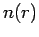
One particle reduced density matrix,

${\mathcal{O}}$

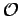
Operator in quantum mechanics,

$p$

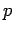
Pressure,

$P(s\to s')$

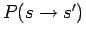
Probability for MC step $s\to s'$,

${\mathcal{P}}$

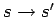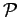
Permutation of identical particles,

$Q$

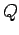
Electronic charge of one ion,

$\pi(s)$

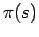
Probability of state $s$,

$\left\vert\Psi \right>$

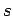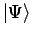
Hilbert vector,

${\bf r}$

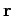
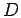$D$ dimensional coordinate vector,

${\bf R}$

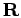
Set of coordinates of 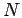$N$ particles in 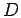$D$ dimensions,

$r_s$

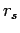
density parameter $a/a_0$,

$\rho$

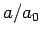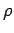
Density matrix,

$\varrho$

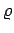
Mass density $mN/{V^{\!\!\!\!\!\!\:^\diamond}}$,

$S$

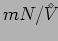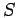
Action in path integral,

$s$

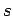
State in configuration space,

$T$

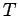
Temperature,

$T_F$

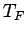
Fermi temperature $E_F/k_B$,

$T(s\to s')$

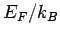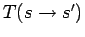
Sampling distribution for MC step $s\to s'$,

$t$

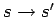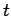
Imaginary time,

$\tau$

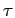
Time step in path integrals,

$\theta$

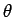
Degeneracy parameter $T/T_F$,

$w$

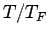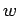
Width parameter in Gaussian density matrix,

$\mathcal{V}$

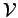
Potential energy operator,

$V$

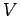
Potential energy,

${V^{\!\!\!\!\!\!\:^\diamond}}$

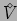
Volume of the simulation cell $L^D$,

$Z$

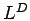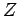
Canonical partition function.