EOS author:	Burkhard Militzer	Email: militzer at berkeley dot edu
In close collaboration with	William B. Hubbard

      
Recommended citations:

[1] B. Militzer, W. B. Hubbard, "Ab Initio Equation of State for Hydrogen-Helium Mixtures with Recalibration of the Giant-Planet Mass-Radius Relation", Astrophysical Journal 774 (2013) 148. (Astro-ph).
[2] B. Militzer, "Equation of state calculations of hydrogen-helium mixtures in solar and extrasolar giant planets", Physical Review B 87 (2013) 014202.

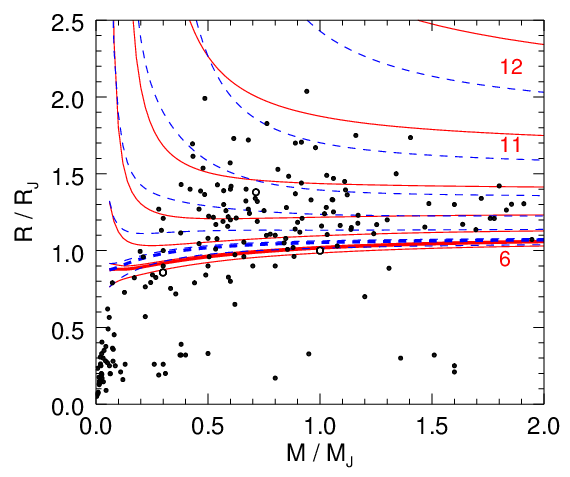Giant planet mass-radius relation in Jupiter units (figure 12 in Ref. [1])

Using density functional molecular dynamics simulations, we determine the equation of state  (EOS) for hydrogen-helium mixtures spanning density-temperature conditions typical of giant planet interiors. In our manuscript [1], a comprehensive equation of state table with 391 density-temperature points is constructed and the results are presented in form of two-dimensional free energy fit for interpolation. This web page was setup togive everyone access to our EOS points, the coefficients of the free energy fit, and our free energy interpolation code, which is currently written in Fortran 77. A C++ version could be constructed if there is sufficient demand. We found that our DFT-MD simulations led to significant EOS corrections (for details see [1]) to the well-known, semi-analytical Saumon-Chabrier-van Horn EOS, which gave rise to a recalibration of mass-radius relationship (left figure) in solar and extrasolar giant planets.

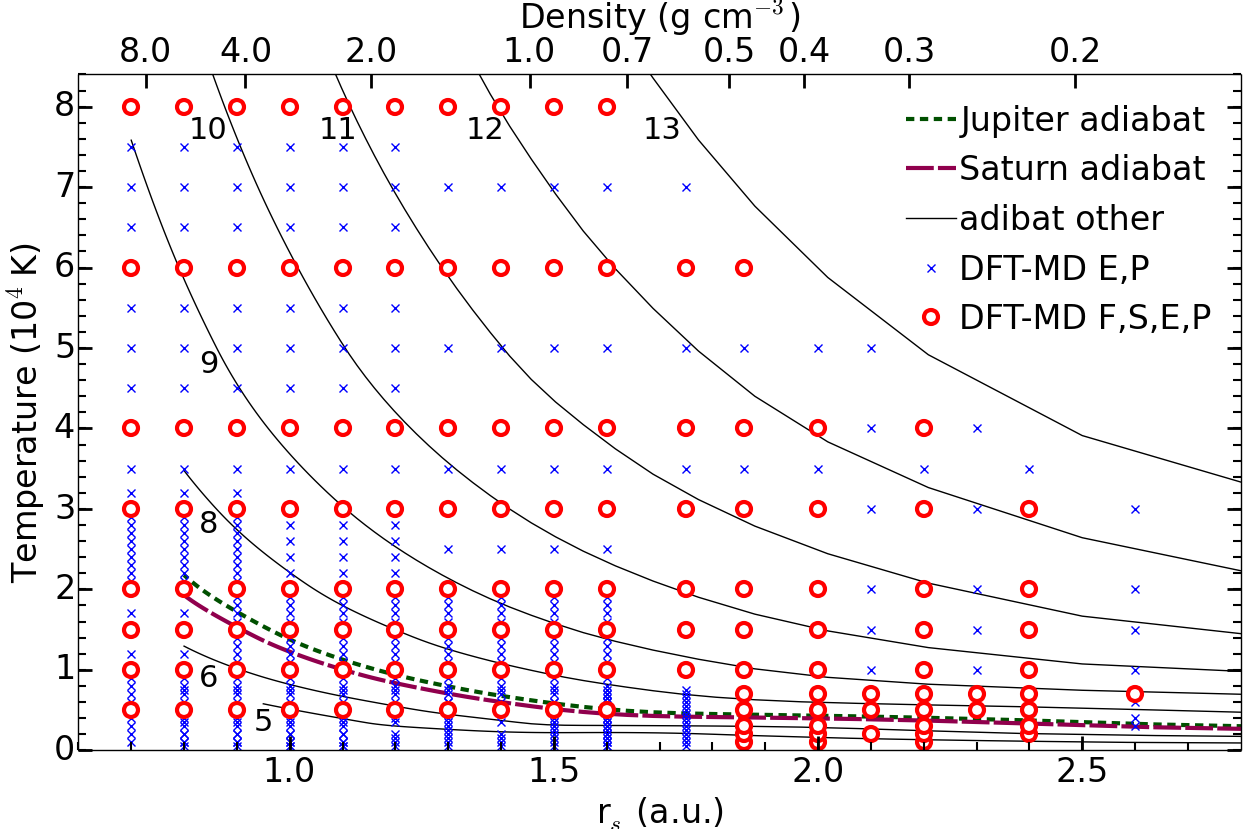Temperature-density conditions were DFT-MD simulations were performed (figure 1 in Ref. [1])

Comments: This table contains the pressure, internal energy, entropy, and free energy from our ab initio simulations a hydrogen-helium mixture of a solar-type composition with 18 helium in 220 hydrogen atoms. The helium mass fraction is Y=0.245. The density parameter rs is given by 4/3*pi*rs3=V/Ne where Ne is total number of electrons (bound and free) in volume V. The number density of electrons is n=Ne / V. The fit uses atomic units:   rs is given Bohr radii = 5.29177208607e–11 m   F and E are given in Hartree/electron = 4.35974380267e–18 J   S is given in kb/electron where kb is Boltzmann's constant. Here is an example for an energy conversion. The zero of energy was set to state of isolated, neutral atoms at rest, which is constistent with the convention in the VASP simulation code. The groundstate energy is the isolate hydrogen molecule using PBE including zero-point energy then becomes -0.2386100 Hartree per molecule. Limitations: In density, the fit ranges from rs=3.581 to 0.526 [density = 0.06696 ... 19.97757 g/cc, log10(density)=–1.1742 ... 1.3005]. So an alternative EOS table is needed to model the outer envelop of a giant planet where the H-He mixture is at a lower density.  The temperature range of the fit is 500 ... 120,000 K [log10(T)=2.6990 ... 5.0792] but only 1,000 ... 80,000 K is based on data from DFT-MD simulations. Elsewhere we use an extrapolation.

A number of files can be downloaded:

Date	File description	Download link
01-29-13	Fortran 77 code that prints a number of EOS points based on the free energy interpolation	eoshhe_01-29-13.f
01-29-13	Output of EOS code	eos.out
01-29-13	Very similar Fortran 77 code that prints the adiabats rather than the EOS points	adhhe_01-29-13.f
01-29-13	Output of adibat code	ad.out
01-31-13	Machine readable table of the original EOS points derived from DFT-MD simulations	EOS.txt
01-31-13	Machine readable table of the 2D spline coefficients	EOS_fit.txt

Any standard Fortran 77 compiler should work, e.g. GNU compiler:
     gfortran adhhe_01-29-13.f -o ad
     ad > my_ad.out
Then compare my_ad.out with the provided ad.out. All EOS information is encoded in the f77 file. So no external data files need to be read in during execution.